6. Кореляція процесів на вході та виході лінійної системи. Оцінка статистичного зв'язку "білого шуму" та реакції на нього лінійної системи.
Зрозуміло,
що
реакція
ЛІВ системи
та дія
на неї
є взаємозалежними, а отже статично
залежними і корельованими. Природа та
характер такого статистичного зв’язку
відображається, як відомо, взаємними
кореляційними функціями. Зокрема, для
нецентрованих процесів функція
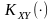визначає
статистичний зв’язок
між процесом на вході та реакцією на
виході;
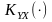- статистичний
зв’язок
між процесом
на виході ЛІВ системи та
на її вході.
Відомо,
що
за
властивостями
.
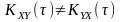Водночас,
справджується властивість дзеркальної
симетрії:
.
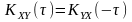Стаціонарний
режим системи. За
визначенням
взаємна кореляційна функція
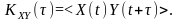Враховуючи
те, що
для стаціонарного
режиму
,
,
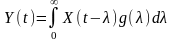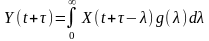дістанемо:
.
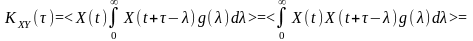
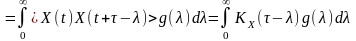Зазначимо, що спочатку внесено під знак інтегралу оскільки не залежить від змінної інтегрування, а потім за відомими правилами під знак інтегралу внесена і операція усереднення.
Таким
чином,
взаємна
кореляційна функція
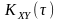є згорткою кореляційної функції вхідного
процесу
і імпульсної характеристики ЛІВ системи
:
.
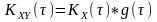Взаємна кореляційна функція
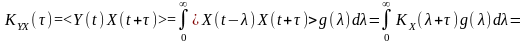
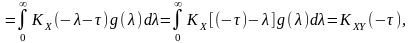
де
враховано, що
,
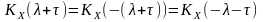оскільки
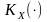є функцією парною відносно аргументу.
Приклад.
ЛІВ
система має імпульсну характеристику
.
На вході такої системи діє білий шум
X(t).
Знайти
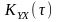та
.
Відомо, що кореляційна функція білого шуму . Тоді взаємна кореляційна функція
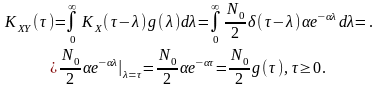
Згідно
з фізичною реалізованістю системи
для всіх
значень
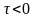функція
.
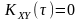Отже,
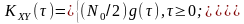
З урахуванням властивості дзеркальної симетрії
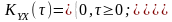
Дійсно,
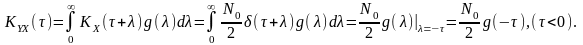
Отже,
у
разі дії білого шуму ступінь статистичного
зв’язку
між стаціонарними дією
та реакцією
ЛІВ системи визначається властивостями
системи (імпульсною характеристикою).
Отриманим
результатом часто користуються для
експериментального визначення імпульсної
характеристики чи її параметрів за
кореляційною функцією. Так,
наприклад,
такий
параметр ЛІВ системи,
як тривалість
імпульсної характеристики,
визначає
інтервал кореляції,
оскільки
,
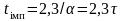де
– постійна часу системи. Прилади для
визначення кореляційних функцій
називають корелометрами.
Режим нестаціонарної реакції. Згідно з інтегралом згортки та взаємна кореляційна функція
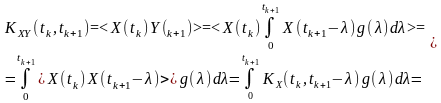
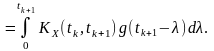
Останні співвідношення можна записати і через величину , що визначає відстань між перерізами і :
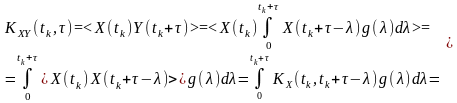
Приклад.
На вході ідеального інтегратора діє
стаціонарний білий шум N(t)
з кореляційною функцією
.
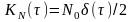Визначити взаємну кореляційну функцію
вхідного N(t)
та вихідного Y(t)
процесів.
Імпульсна характеристика ідеального інтегратора
.
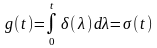Оскільки реакція є нестаціонарною, то відповідно до (11.23) дістанемо шукану взаємну кореляційну функцію:
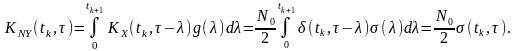
ПІДСУМКИ |
|
1.У разі дії білого шуму ступінь статистичного зв’язку між стаціонарними дією та реакцією ЛІВ системи визначається властивостями системи (імпульсною характеристикою).
|
2.Взаємна кореляційна функція є згорткою кореляційної функції вхідного процесу і імпульсної характеристики ЛІВ системи у стаціонарному режимі її функціонування. 3. Формули для визначення взаємної кореляційної функції реакції та дії ЛІВ системи: - для стаціонарної реакції
- для нестаціонарної реакції
|
;
.
Лекція 15. Спектр реакції лінійних ланок та систем.
Аналіз у частотній області. Визначення спектральної щільності потужності реакції лінійної системи на дію СВП. Спектр реакції та середній квадрат (дисперсія). Спектральний аналіз інтегруючої системи при дії "білого шуму". Енергетичний спектр реакції ідеального диференціатора.
Шумова смуга лінійної системи: визначення та практична значимість. Обчислення шумової смуги системи у частотній області. Співвідношення між умовною смугою пропускання та шумовою смугою лінійної системи. Визначення шумової смуги системи у часовій області.
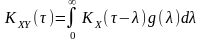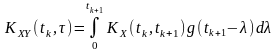