5.Автокореляційна функція реакції. Згортка акф дії та імпульсної характеристики.

Стаціонарної реакція. За визначенням для нецентрованого випадкового стаціонарного процесу автокореляційна функція 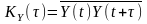У разі, якщо її значення 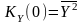визначає середній квадрат стаціонарного процесу. З урахуванням стаціонарності та визначення середнього квадрата

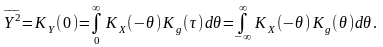
Тоді, очевидно, для будь-якого

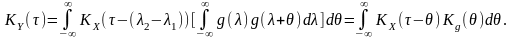
АКФ стаціонарної реакції ЛІВ системи є згорткою в нескінченних межах АКФ діючого стаціонарного процесу та кореляційної функції імпульсної характеристики системи.

Приклад. Припустімо, що на вході ЛІВ системи діє випадковий процес на зразок білого шуму з .

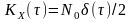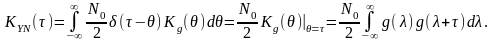
Таким чином, у разі дії на ЛІВ стійку систему білого шуму кореляційна функція стаціонарного відгуку пропорційна кореляційній функції її імпульсної характеристики (кореляційному інтегралу).

Приклад. На вході системи діє флуктуаційна напруга Х(t) у вигляді білого шуму з нульовим середнім та функцією кореляції . Знайти кореляційну функцію вихідної напруги Y(t) в стаціонарному режимі та інтервал кореляції.

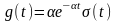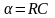Імпульсна характеристика такої системи , де . Кореляційна функція реакції

.

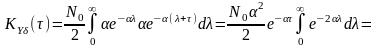
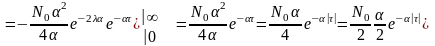У підсумку враховано, що 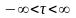, а також те, що кореляційна функція є парною: .

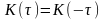Природно, що значення функції кореляції в нулі 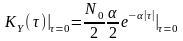- є середнім квадратом реакції, яке збігається у цьому разі з дисперсією .

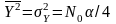Інтервал кореляції

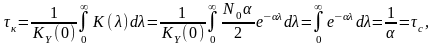
Система, є частковим випадком ЛІВ системи з інтегрувальними властивостями.

Отже, у разі збудження ЛІВ інтегруючої системи першого порядку білим шумом у стаціонарному режимі її вихідний процес характеризується експоненціальною автокореляційною функцією та інтервалом кореляції, що має порядок постійної часу системи.

Білий шум визначається нульовим інтервалом кореляції, а отже, некорельованістю його миттєвих значень у найближчих перерізах, що можливо тільки за дуже швидкої зміни в часі його реалізацій.

Інтервал кореляції реакції інтегруючої системи не дорівнює нулю, а тому вихідний процес розвивається більш повільно. Швидкість його розвитку в часі визначається тільки параметрами системи, зокрема, постійною часу.

Нестаціонарна реакція. За означенням автокореляційна характеристика нестаціонарної реакції

.

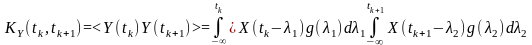Внесемо операцію усереднення під знак інтегралу:

.

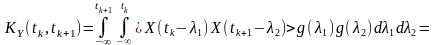
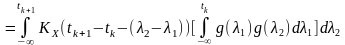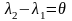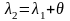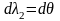Зафіксуємо та введемо нову змінну . Тоді , , а

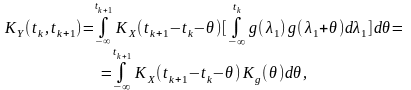
де кореляційний інтеграл тепер

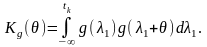
Приклад. Знайти кореляційну функцію реакції інтегруючої системи з імпульсною характеристикою у разі дії на неї процесу X(t), кореляційна функція якого , вважаючи реакцію нестаціонарним випадковим процесом.

Кореляційний інтеграл

=

.

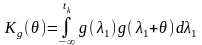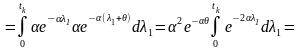
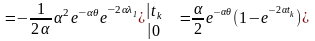З урахуванням стробувальної властивості -імпульсу кореляційна функція реакції

.

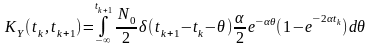
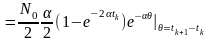Остаточно, з урахуванням властивості парної симетрії кореляційної функції

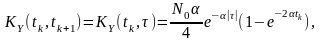
де .

Значення кореляційної функції для визначає середню потужність нестаціонарної реакції:

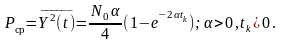
Зазначимо, що в теорії систем – коефіцієнт загасання, наприклад, інтегруючого RC – кола першого порядку з імпульсною характеристикою , 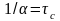– постійна часу системи. Крім того, 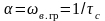визначає ширину смуги пропускання 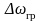системи першого порядку на рівні половинної потужності:

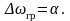
Тоді, середній квадрат стаціонарної реакції інтегруючої системи першого порядку на дію білого шуму

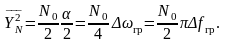
Значення середнього квадрату (середньої потужності) реакції інтегруючої системи зростає пропорційно збільшенню її смуги пропускання .

Подібна ситуація є характерною у разі, коли ширина спектра випадкового процесу на вході ЛІВ системи значно перевищує її смугу пропускання.

Ширина спектра діючого процесу на вході ЛІВ системи значно більше за її смугу пропускання, допустимою є апроксимація дії процесом на зразок ”білий шум ”.

У цьому разі значно зменшується трудоємність обчислень при збереженні допустимої точності. Так, наприклад, при застосуванні підсилювача з великим коефіцієнтом підсилення в смузі частот 10 МГц найбільш інтенсивною складовою його шумів є та, що зумовлена дробовим ефектом (дробовий шум), ширина спектральної щільності якої досягає 1000 МГц. Відношення 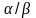при цьому складає 0,01, а похибка від апроксимації дробового шуму білим шумом не перевищує 1%.

ПІДСУМКИ
1. У разі збудження ЛІВ інтегруючої системи білим шумом у стаціонарному режимі динаміка вихідного процесу визначається тільки параметрами системи, зокрема, постійною часу. 2. Якщо ширина спектра діючого процесу на вході ЛІВ системи значно більше за її смугу пропускання, допустимою є апроксимація дії процесом на зразок білий шум.	3. АКФ стаціонарної реакції ЛІВ системи є згорткою в нескінченних межах АКФ діючого стаціонарного процесу та кореляційної функції імпульсної характеристики системи. 4. Значення середнього квадрата (середньої потужності) реакції інтегруючої системи на дію білого шуму зростає пропорційно збільшенню її смуги пропускання.