
- •1.Закони розподілу випадкових процесів процесів
- •2. Одновимірні інтегральний та диференціальний закони розподілу
- •Неперервного (а), дискретного (б) та змішаного (в) процесів.
- •Закони розподілу ймовірностей дискретного процесу.
- •Щільності (б) ймовірностей дискретного процесу.
- •1 Загальна характеристика моментних функцій
- •2.Порядок та розмірність момент них функцій
- •3.Початкові моментні функції. Структура формул
- •4 Одновимірні моментні функції першого порядку
- •1.Одновимірні моментні функції другого порядку
- •Очікуваннями і різними дисперсіями.
- •Процесів із однаковими математичними очікуваннями
- •Початковою фазою: а – реалізації випадкового процесу;
- •1.Обчислення одновимірних моментних функцій за характеристичними.
- •2. Поновлення одновимірних характеристичних функцій за моментними.
- •6.1 Види статистичної залежності
- •Кореляцією (б) та некорельовані величини (в).
- •6.2 Двовимірні моментні функції другого порядку
- •7.1 Вкф двох випадкових процесів
- •Його кореляційна функція (б).
- •7.2 Нормовані кореляційні функції.
- •7.3 Особливості кореляційних характеристик
- •1 Визначення стаціонарності у вузькому та широкому значеннях
- •8.2 Математичне очікування,середній квадрат,дисперсія свп
- •8.3 Властивості акф нецентрованого та центрованого свп
- •Процесу (а) та похідної від нього (б).
- •Випадкового процесу.
- •3.Практичне застосування вкф для вирішення проблем виділення слабкого сигналу з суміші.
- •1. Визначення ергодичних випадкових процесів
- •2. Достатні умови ергодичності свп. Умова Слуцького
- •Спектральні характеристики випадкових процесів
- •1. Постановка задачі спектрального аналізу вп
- •2. Енергетичний спектр нестаціонарного вп та його зв'язок з кореляційною функцією.
- •3.Спектральна щільність потужності свп та її фізичний зміст. Спектр флуктуацій (центрованого) свп. Середній квадрат (дисперсія) та спектр свп.
- •4. Властивості спектральної щільності потужності свп. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп
- •5. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп
- •1. Теорема Вінера-Хінчина. Обмеження, що накладаються на акф свп. Додатньо-визначені акф.
- •1.Постановка задачі кореляційного аналізу лінійних систем при дії свп
- •3.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
- •4.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
- •5.Автокореляційна функція реакції. Згортка акф дії та імпульсної характеристики.
- •6. Кореляція процесів на вході та виході лінійної системи. Оцінка статистичного зв'язку "білого шуму" та реакції на нього лінійної системи.
- •З урахуванням властивості дзеркальної симетрії
- •Дійсно,
- •1.Аналіз у частотній області.
- •4. Спектральний аналіз інтегруючої системи при дії "білого шуму".
- •5. Енергетичний спектр реакції ідеального диференціатора.
- •На нього ідеального диференціатора (б).
3.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
Приклад.
Імпульсна
характеристика ЛІВ системи g(t)=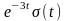 .
На вході системи діє адитивна суміш
білого шуму N(t) з нульовим математичним
очікуванням та постійної складової
.
На вході системи діє адитивна суміш
білого шуму N(t) з нульовим математичним
очікуванням та постійної складової
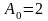 В.
Обчислити математичне очікування
стаціонарного випадкового процесу на
виході такої системи.
В.
Обчислити математичне очікування
стаціонарного випадкового процесу на
виході такої системи.
Згідно
з принципом суперпозиції реакція системи
складається з суми двох складових
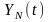 та
та
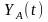 ,
де
–
реакція системи на дію білого шуму
,
де
–
реакція системи на дію білого шуму
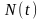 ;
- реакція на дію постійної складової.
;
- реакція на дію постійної складової.
За
властивостями математичне очікування
процесу
є сумою математичних очікувань його
складових:
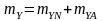 .
Оскільки білий шум характеризується
нульовим математичним очікуванням
.
Оскільки білий шум характеризується
нульовим математичним очікуванням
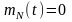 ,
то
,
то
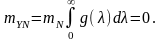
Постійній
складовій
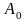 в
реакції відповідає складова
,
математичне очікування якої
в
реакції відповідає складова
,
математичне очікування якої
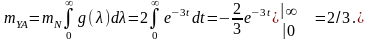
Остаточно,
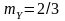 .
.
Середній
квадрат реакції.
Для визначення середнього квадрата
(середньої потужності)
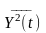 реакції потрібно обчислити математичне
очікування добутку двох інтегралів та
ввести дві змінні інтегрування.
реакції потрібно обчислити математичне
очікування добутку двох інтегралів та
ввести дві змінні інтегрування.
Тоді у разі нестаціонарної реакції
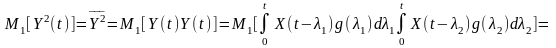
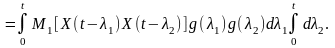
Середнє
статистичне добутку
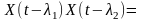
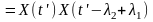 є автокореляційною функцією випадкового
процесу
з відповідним аргументом:
є автокореляційною функцією випадкового
процесу
з відповідним аргументом:
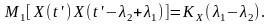
Тоді
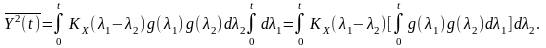
Введемо
нову змінну
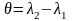 ,
тоді
,
тоді
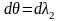 ,
а
,
а
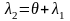 ,
за умови, що
,
за умови, що
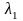 зафіксовано. В результаті отримаємо:
зафіксовано. В результаті отримаємо:
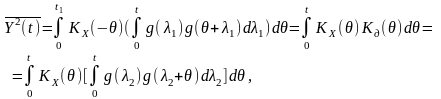
де
враховано властивість парної симетрії
АКФ функції: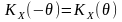 .
.
Інтеграл
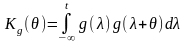
називають кореляційним інтегралом або автокореляційною функцією імпульсної характеристики ЛІВ системи , як детермінованого процесу.
4.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
Приклад. Імпульсна характеристика ЛІВ системи g(t)= . На вході системи діє адитивна суміш білого шуму N(t) з нульовим математичним очікуванням та постійної складової В. Обчислити математичне очікування стаціонарного випадкового процесу на виході такої системи.
Згідно з принципом суперпозиції реакція системи складається з суми двох складових та , де – реакція системи на дію білого шуму ; - реакція на дію постійної складової.
За властивостями математичне очікування процесу є сумою математичних очікувань його складових: . Оскільки білий шум характеризується нульовим математичним очікуванням , то
Постійній складовій в реакції відповідає складова , математичне очікування якої
Остаточно, .
Приклад.
На конденсатор ємності С діє флуктуаційний
струм I(t)
як стаціонарний процес на зразок білого
шуму з автокореляційною функцією
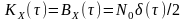 .
Визначити
дисперсію випадкової напруги U(t)
на
конденсаторі.
.
Визначити
дисперсію випадкової напруги U(t)
на
конденсаторі.
За
властивостями дисперсія
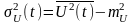 .
Математичне очікування випадкової
вихідної напруги набуває нульового
значення, оскільки середнє статистичне
значення білого шуму дорівнює нулю.
Отже, дисперсія напруги збігається з
середнім квадратом.
.
Математичне очікування випадкової
вихідної напруги набуває нульового
значення, оскільки середнє статистичне
значення білого шуму дорівнює нулю.
Отже, дисперсія напруги збігається з
середнім квадратом.
Напруга на конденсаторі з використанням його лінійної моделі пропорційна інтегралу струму, що протікає через нього. Тоді імпульсна характеристика такої системи
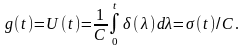
Відповідно до (11.10) та з урахуванням (11.9) кореляційний інтеграл
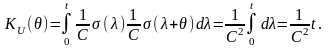
Під час обчислення інтегралу враховано, що добуток двох одиничних ступінчатих функцій із вказаними аргументами, відмінний від нуля і дорівнює одиниці тільки на інтервалі інтегрування [0, t].
Середній квадрат випадкової напруги
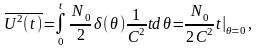
де
враховано
стробувальну
властивість
дельта-функції.
У разі, якщо
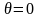 ,
то
,
то
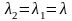 ,
тоді
,
тоді
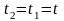 .
.
Остаточно дисперсія випадкової напруги на конденсаторі
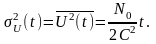
Залежність дисперсії від часової змінної t вказує на нестаціонарність випадкової напруги на конденсаторі, що узгоджується з раніше отриманим висновком: результатом інтегрування стаціонарного процесу є нестаціонарний процес.
Цей приклад вказує на можливість спрощення розрахунків, якщо кореляційна функція діючого процесу є дельтоподібною, наприклад, коли вхідна дія є білим шумом. Тоді результат фактично визначається кореляційним інтегралом, а точніше, імпульсною характеристикою системи, а отже її властивостями.
Дійсно, кореляційна характеристика білого шуму .
Середній квадрат реакції ЛІВ системи
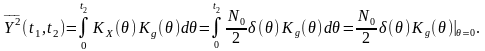
Якщо , то , а . Тоді
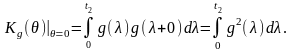
Остаточно,
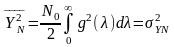 .
.
Середній квадрат реакції ЛІВ системи (середня потужність реакції) на дію білого шуму прямо пропорційний площі, обмеженій графіком квадрата її імпульсної характеристики та відповідним відрізком осі абсцис.
Для стаціонарної реакції у всіх наведених співвідношеннях для нестаціонарної реакції слід замість верхньої межі при інтегруванні брати ∞.
ПІДСУМКИ |
|
1.Математичне очікування реакції на виході ЛІВ системи дорівнює нулю за нульового значення середнього статистичного дії або якщо система придушує постійну складову вхідного процесу. 2. У разі, якщо кореляційна функція діючого процесу є дельтоподібною середній квадрат реакції системи її імпульсною характеристикою.
|
3. Середнє статистичне значення вхідного випадкового процесу під час перетворення ЛІВ системою змінюється прямо пропорційно інтегралу від імпульсної характеристики системи у разі, якщо дія є стаціонарною, та перехідній характеристиці системи за нестаціонарної дії: 4. Формули: - кінцеве значення перехідної характеристики;
|

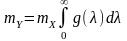 -
математичне очікування стаціонарної
реакції;
-
математичне очікування стаціонарної
реакції;
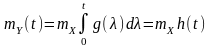 -
математичне очікування нестаціонарної
реакції;
-
математичне очікування нестаціонарної
реакції;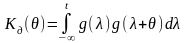 -
кореляційний інтеграл.
-
кореляційний інтеграл.