1.Постановка задачі кореляційного аналізу лінійних систем при дії свп

Із попереднього матеріалу відомо що:

ймовірнісний опис випадкового процесу грунтується на законах розподілу ймовірностей(функції розподілу ймовірностей та щільності ймовірностей);

а статистичний – на характеристиках усереднення за ансамблем реалізацій (моментні функції різних порядків та спектри).

З’ясуємо яким чином ці методи можуть бути застосовані для визначення властивостей реакції системи під час дії на неї випадкового збудження.

Вибір того чи іншого підходу зумовлюється як властивостями системи, так і властивостями діючого процесу.

Як підтверджує практика, в будь-якому випадку статистичний підхід є більш ефективним: визначення багатовимірних імовірнісних характеристик реакції за заданими багатовимірним імовірнісними характеристикам дії з урахуванням властивостей системи є дуже складним завданням, вирішення якого є проблематичним.

Тому зупинимося на оцінці перетворень випадкових процесів лінійними системами в рамках спектрально-кореляційної теорії, яка базується на статистичному підході до опису випадкових

процесів, тобто на використанні таких його характеристик, як математичне очікування, середній квадрат (дисперсія), кореляційна функція та спектральна щільність. Крім того, в основному будемо розглядати вхідні процеси , які є тільки стаціонарними в широкому значенні. Як відомо, це передбачає незалежність від часового аргументу математичного очікування та середнього квадрату 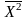або дисперсії , а також інваріантність кореляційної функції ( відносно моментів часу , в яких визначаються перерізи процесу .

Властивості лінійної детермінованої системи у часовій області описуються часовими характеристиками, а у частотній - частотними, кожна з яких є своєрідним відображенням оператора зв’язку 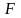діючого процесу (сигналу) та реакції 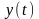. У разі, якщо оператор не залежить від часової змінної , лінійна система називається стаціонарною або лінійною системою з постійними параметрами. Коли така залежність має місце, то маємо нестаціонарну лінійну або просто параметричну систему.

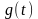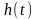До часових характеристик лінійної системи належить імпульсна та перехідна характеристики, які є відгуками системи за нульових початкових умовах на дію, що описується функцією Дірака 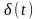та функцією Хевісайда відповідно (рис. 1).

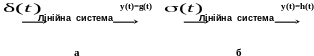
Рисунок 1 - До визначення імпульсної (а) та перехідної (б) характеристик.

Для систем, що фізично реалізуються, часові характеристики задовольняють такі співвідношення:

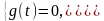
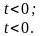
Вважається, що лінійна система є стійкою, якщо

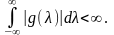
З фізичного погляду - у стійкій системі власні коливання з часом зменшуються до нуля або не перевищують деякого рівня.

Будемо вважати, що на вході лінійної інваріантної в часі (ЛІВ) системи діє випадковий процес з математичним очікуванням , середнім квадратом 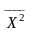(дисперсією ) та функцією автокореляції . Властивості ЛІВ системи подамо її імпульсною або перехідними характеристиками, які є детермінованими (невипадковою) функцією.

Тоді завдання кореляційного аналізу тоді полягає у визначенні відповідних статистичних характеристик реакції : математичного очікування , середнього квадрату 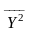(дисперсії 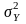), автокореляційної 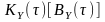та взаємно кореляційних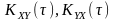 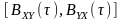функцій.

Якщо – певна реалізація випадкового процесу , то відповідна реалізація випадкової реакції може бути визначена на основі однієї з відомих форм інтеграла Дюамеля (згортки).

ПІДСУМКИ
1. Статистичний підхід до визначення властивостей реакції лінійної системи під час дії на неї випадкового збудження є більш ефективним за ймовірнісний.	2. Умова стійкості лінійної системи:

2.МО та середній квадрат реакції лінійної системи на дію СВП. Кореляційний інтеграл.

Математичне очікування реакції. За нульових початкових умов відповідно до однієї з модифікацій методу інтеграла Дюамеля (згортки) нестаціонарна реакція ЛІВ системи на випадкову дію

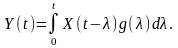
Якщо реакція є стаціонарним випадковим процесом, тоді

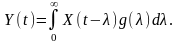
Математичне очікування реакції обчислимо, здійснивши операцію усереднення обох частин :

;

.

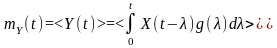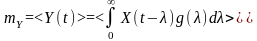Внесемо символ статистичного усереднення під знак інтеграла, що завжди можливе за таких умов:

– деякий випадковий процес (або деяка функція від нього), а 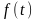– невипадкова функція часу, то середнє статистичне

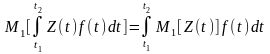
за умови, що

1)

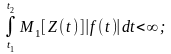
2) процес на інтервалі 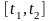, в загальному випадку нескінченному, є обмеженим, тобто таким, що його миттєві значення не набувають нескінчених значень.

У випадку, що розглядається, ці умови виконуються. Дійсно, для реальних ситуацій миттєві значення процесу 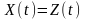не можуть набувати нескінчених значень.

Для стаціонарного діючого процесу середнє статистичне 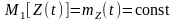, тобто не залежить від часової змінної . З урахуванням умови стійкості системи і того, що 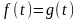,дістанемо

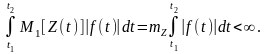
Змінивши послідовність операцій інтегрування та усереднення, отримаємо:

- для стаціонарної реакції

;

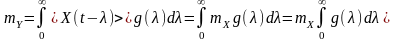- для нестаціонарної реакції

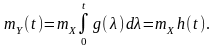
Середнє статистичне значення вхідного випадкового процесу під час перетворення ЛІВ системою змінюється прямо пропорційно площі під графіком імпульсної характеристики системи у разі, якщо дія є стаціонарною, та перехідній характеристиці системи за нестаціонарної дії.

Як відомо із теорії лінійних систем площа, обмежена імпульсною характеристикою в межах 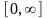, дає кінцеве значення перехідної характеристики. Перехідна характеристика є реакцією лінійної системи за нульових початкових умов на комутацію постійного процесу одиничної амплітуди, а її кінцеве значення

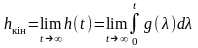
визначає коефіцієнт передачі постійної складової дії в усталеному постійному режимі. Тоді дійдемо таких висновків:

1.постійна складова стаціонарного вихідного процесу ЛІВ, як реакції на стаціонарний процес , дорівнює добуткові постійної складової дії на коефіцієнт передачі системи в усталеному постійному режимі;

математичне очікування реакції на виході ЛІВ системи дорівнює нулю за нульового значення середнього статистичного дії або якщо система придушує постійну складову вхідного процесу.

Приклад. Математичне очікування випадкової реакції ЛІВ RL-кола, зображеного на рис.2, а на дію гармонічного процесу, середньостатистичне значення якого дорівнює нулю, також набуває нульового значення незалежно від того чи є реакція стаціонарною, чи ні.. Це безпосередньо випливає з формул

◙

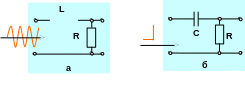
Рисунок 2 - Приклади лінійних систем із нульовим математичним очікуванням стаціонарної реакції.

Приклад. Стаціонарна випадкова напруга на резистивному елементі в ЛІВ системі, зображеної на рис.2, б, характеризується нульовим математичним очікуванням навіть за умови, що середньостатистичне значення стаціонарної дії, відмінне від нуля. Підтвердженням цього слугують такі міркування. При 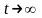система переходить в постійний режим. Ємнісний елемент не пропускає постійний струм, що спричинює на резистивному елементі нульову напругу.

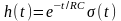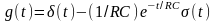Перехідна характеристика системи , а імпульсна, як похідна від перехідної, - . Кінцеве значення

перехідної характеристики дорівнює нулю. Відповідно математичне очікування стаціонарної реакції набуває нульового значення.

Середнє статистичне значення нестаціонарної реакції .
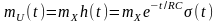