1. Теорема Вінера-Хінчина. Обмеження, що накладаються на акф свп. Додатньо-визначені акф.

Радянським ученим А.Я. Хінчиним та американським Н. Вінером доведена теорема щодо взаємозв’язку між кореляційними та спектральними характеристиками випадкових стаціонарних процесів. Згідно з цією теоремою спектральна щільність потужності ( ) стаціонарного нецентрованого (центрованого ) процесу та автокореляційна функція 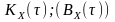пов’язані між собою інтегральним перетворенням Фур’є:

- для нецентрованого стаціонарного процесу

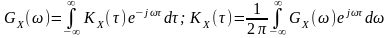; (13.1)

- для центрованого стаціонарного випадкового процесу

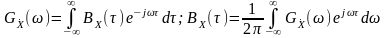. (13.2)

Однозначно пов’язані кореляційна функція і спектральна щільність потужності характеризують випадковий процес у двох аспектах - статистичним зв’язком миттєвих значень процесу в неспівпадаючих перерізах та спектрально.

Маємо аналогію між часовим та спектральним поданням детермінованих процесів, але на відміну від останніх інтегральні співвідношення (13.1) та (13.2) відображають зв’язок не власне процесу, а функції, що є мірою статистичного зв’язку між миттєвими значеннями випадкового процесу та його спектральною характеристикою.

Відмітимо ряд наслідків теореми Вінера-Хінчина.

Значення спектральної щільності потужності на нульовій частоті (початкове значення) дорівнює інтегралу від автокореляційної функції:

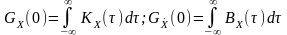. (13.3)

Початкове значення автокореляційної функції пропорційне інтегралу від спектральної щільності і дорівнює середній потужності нецентрованого або дисперсії центрованого процесу:

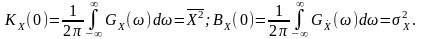(13.4)

Для доведення (13.4) у співвідношеннях (13.1) та (13.2) достатньо покласти .

Автокореляційна функція стаціонарного випадкового процесу і сигналу є додатньо визначеною.

Виходячи з того, що спектральна щільність ( ) є невід’ємною функцією частоти, згідно з (13.1) та (13.2) пряме перетворення Фур’є від автокореляційної функції 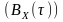повинно бути також невід’ємним. Функції, які задовольняють зазначену умову, і називаються додатньо визначеними.

Так, зокрема, функція

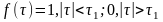
у вигляді прямокутника, не може бути кореляційною.

Дійсно, пряме перетворення Фур’є такої функції

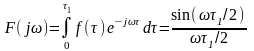
набуває як додатних, так і від’ємних значень.

Приклад. Визначити спектральну щільність потужності випадкового процесу з рівномірним законом розподілу випадкової фази .

Д ля такого процесу математичне очікування , середній квадрат і дисперсія 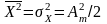, а АКФ

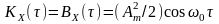
Отже, це стаціонарний у широкому значенні випадковий процес, який називають монохроматичним СВП.

Тоді згідно з (13.1) спектральна щільність потужності такого процесу

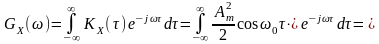
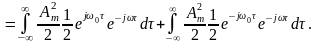
Відповідно до властивостей перетворення Фур’є

.

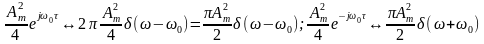Остаточно .

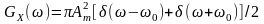Таким чином, спектральна щільність монохроматичного СВП складається з двох дельтоподібних складових однакової площі, зсунутих в точки з частотами 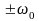(рис. 13.1).

Формули (13.1) та (13.2) можна записати більш компактно в тригонометричній формі, якщо врахувати парність кореляційних та спектральних характеристик:

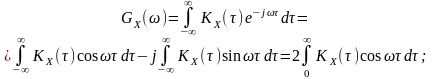(13.5)

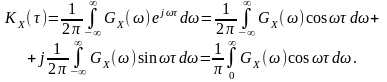(13.6)

Під час перетворень ураховано подання функції 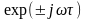через косинус та синус згідно з формулою Ейлера, властивості парності косинуса та непарності синуса, а також те, що в симетричних межах інтеграл від непарної функції дорівнює нулю, а парної - подвійному значенню інтеграла в односторонніх межах.

Перехід до одностороннього спектра веде до таких співвідношень:

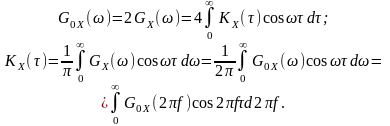(13.7)

2. Спектрально-кореляційна структура СВП типу "білий шум". Приклад. Стаціонарний процес Х(t) характеризується рівномірним спектром (рис. 13.2, а) 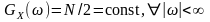. Визначити автокореляційну функцію процесу.

Виходячи з того, що не містиь -особливостей, математичне очікування такого процесу дорівнює нулю: .

Згідно з теоремою Хінчина-Вінера автокореляційна функція

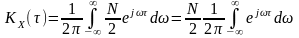. (13.8)

Як відомо з теорії узагальнених функцій, до яких відноситься і дельта-функція, .

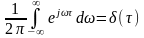Т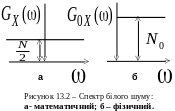 оді 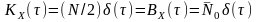АКФ заданого процесу відмінна від нуля при . Отже, миттєві значення процесу в неспівпадаючих перерізах, розміщених на нескінченно малій відстані один від одного, є некорельованими. Останнє означає необмежено велику зміну реалізацій такого процесу в часі.

Початкове значення функції кореляції 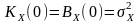. Отже, процес із рівномірним спектром потужності в нескінченному інтервалі частот характеризується нескінченною середньою потужністю.

ПІДСУМКИ

1.Однозначно пов’язані кореляційна функція і спектральна щільність потужності характеризують випадковий стаціонарний процес у двох аспектах - статистичним зв’язком миттєвих значень процесу в неспівпадаючих перерізах та спектрально. 2.Спектр потужності стаціонарного процесу можна визначити за його АКФ у разі, якщо АКФ задовольняє умову додатної визначеності. 3. У разі, якщо миттєві значення випадкового процесу в неспівпадаючих перерізах, розміщених на нескінченно малій відстані один від одного, є некорельованими, то такий процес . характеризується необмежено великою зміною його реалізацій в часі.

4. Початкове значення спектральної щільності потужності дорівнює інтегралу від автокореляційної функції: . 5. Початкове значення автокореляційної функції пропорційне інтегралу від спектральної щільності і дорівнює середній потужності нецентрованого або дисперсії центрованого процесу:

3.Ширина спектру СВП. Способи визначення ширини спектра. Ефективна ширина спектра. Зв'язок ширини спектра та інтервалу кореляції.

Р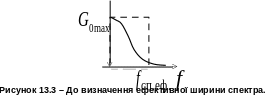 озглянемо стаціонарний нецентрований випадковий процес або сигнал, односторонній енергетичний спектр якого 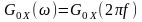набуває максимального значення 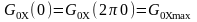на нульовій частоті (рис. 13.3). Площа між графіком спектра та частотною віссю 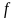дорівнює середньому квадрату 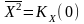, а отже і середній потужності процесу.

Розглянемо також інший процес із рівномірно розподіленим одностороннім спектром у обмеженій смузі частот 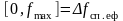, значення якого на всіх частотах дорівнює .

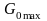Площа, обмежена графіком спектра такого процесу і віссю частот , визначається площею прямокутника 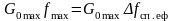. Будемо вважати, що з енергетичного погляду перший та другий процеси є еквівалентними. Тоді

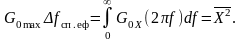
З останнього співвідношення дістанемо:

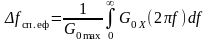. (13.9)

Величина 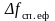називається ефективною шириною енергетичного спектра. Зрозуміло, що подібні співвідношення мають місце і для центрованих процесів.

Ширина двостороннього енергетичного спектра вдвічі більша за значення ефективної ширини: .

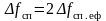Практично використовують і інші підходи до визначення ширини енергетичного спектра випадкових процесів. Зазвичай визначають ширину спектра за відповідним рівнем, наприклад, 0,1 (0,01) .

У будь-якому випадку значення ширини спектра та інтервалу кореляції задовольняють співвідношенню невизначенності:

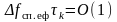. (13.10)

Таким чином, чим вужче енергетичний спектр, тим більше інтервал кореляції і навпаки. А, отже, чим динамічніше процес, тим менше інтервал кореляції, в межах якого значно зменшується кореляційна функція, тим слабкішим є статистичний зв’язок між миттєвими значеннями процесу в неспівпадаючих перерізах, тим ширше енергетичний спектр.

Яскравим прикладом підтвердження цього висновку є білий шум, що характеризується нескінченно великою шириною спектра і нульовим інтервалом кореляції.

Стаціонарний випадковий процес із рівномірно розподіленою спектральною щільністю потужності та дельтоподібною кореляційною функцією називається білим шумом або дельта-корельованим процесом..

Термін «білий шум» образно підкреслює аналогію з білим (природнім) світлом, у якого в межах спектра видимих частот, інтенсивність всіх спектральних складових однакова.Білий шум є абстрактною моделлю. Фізичних процесів подібного типу в природі не існує. Однак, практичне значення такої моделі велике, особливо у разі, якщо енергетичний спектр діючого процесу є рівномірним (постійним) у достатньо широкій смузі частот, причому більш широкій, чим смуга пропускання системи. Зрозуміло, що вид спектра діючого процесу за межами смуги пропускання тоді майже не впливає на параметри вихідного процесу. Тому спектральну щільність діючого процесу можна вважати постійною в усьому частотному діапазоні, а сам процес (діючий) - білим шумом.

Дуже поширеною ідеалізацією реальних явищ є білий шум із обмеженим спектром. Енергетичний спектр цього процесу є рівномірним у кінцевій смузі частот, а за її межами він дорівнює нулю:

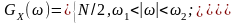(13.11)

Залежно від того, в яких ділянках частотного діапазону зосереджений спектр, а також від співвідношення між його шириною та частотами, що її обмежують, розрізняють:

• низькочастотний квазібілий шум (рис. 13.4, а) із нульовою центральною частотою та крайніми частотами

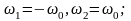
• широкосмуговий квазібілий шум (рис. 13.4, б):

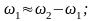
• вузькосмуговий квазібілий шум (рис. 13.4, в):

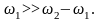
За аналогією з кореляційними функціями вводять поняття нормованих спектральних щільностей потужності як відношення спектральної щільності потужності до середньої потужності для нецентрованого процесу чи дисперсії для процесу центрованого:

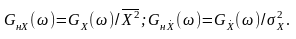
Приклад. Односторонній енергетичний спектр стаціонарного випадкового процесу Х(t) має вигляд:

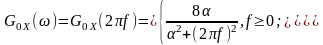
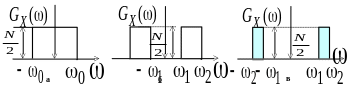
Рисунок 10.6 - Спектри процесів на зразок білого шуму:

а - низькочастотного; б – широкосмугового; в – вузькосмугового.

Визначити, як співвідносяться ефективна ширина спектра і ширина спектральної щільності на рівні

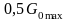
Ефективна ширина спектра

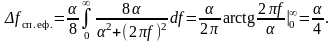
Ширина спектральної щільності за рівнем задовольняє таку умову:

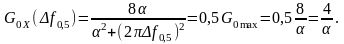
Очевидні перетворення дають, що

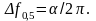
Таким чином, .

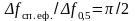ПІДСУМКИ

1. Чим вужче енергетичний спектр, тим більше інтервал кореляції і навпаки. 2. Чим динамічніше процес, тим менше інтервал кореляції, тим слабкішим є статистичний зв’язок між миттєвими значеннями процесу в неспівпадаючих перерізах, тим ширше енергетичний спектр. 2. Білий шум є абстрактною моделлю фізичних процесів. Практична значущість такої моделі велика, особливо у разі, якщо енергетичний спектр діючого процесу є рівномірним у смузі частот, більш широкій, ніж смуга пропускання системи.

4. Формулу, яка встановлює взаємозв’язок між шириною спектра та інтервалом кореляції: .

Лекція 14. Аналіз лінійних ланок та систем в рамках кореляційної теорії.

Постановка задачі кореляційного аналізу лінійних систем при дії СВП. МО та середній квадрат реакції лінійної системи на дію СВП. Кореляційний інтеграл. Статистичні характеристики реакції лінійної системи на дію "білого шуму". АКФ реакції лінійної системи. Згортка АКФ дії та імпульсної характеристики. Кореляція процесів на вході та виході лінійної системи. Оцінка статистичного зв'язку "білого шуму" та реакції на нього лінійної системи.
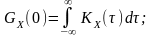
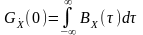