5. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп

Спектральну щільність потужності стаціонарного процесу часто називають двосторонньою спектральною щільністю потужності, двостороннім енергетичним або просто математичним спектром у зв’язку з тим, що визначається такий спектр як для додатних фізичних (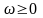 ), так і від’ємних (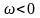 ) значень частоти. Останні, як відомо, фізичного значення не мають.

Односторонній енергетичний спектр або одностороння спектральна щільность потужності 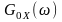, визначається тільки для додатних значень частоти. Односторонній енергетичний спектр ще називають фізичним спектром.

Між одно- та двосторонньою спектральною щільністю потужності є відповідний зв‘язок, що відображається таким співвідношенням:

- для нецентрованого випадкового стаціонарного процесу

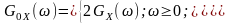(12.17)

- для центрованого випадкового стаціонарного процесу

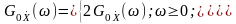(12.18)

Типові графіки математичного та фізичного спектрів зображені на рис. 12.2.

З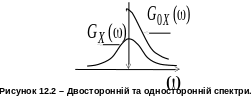 а одностороннім спектром можна завжди обчислити двосторонній:

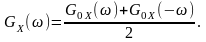
Інтегруванням для діапазону додатних (фізичних) частот за одностороннім енергетичним спектром визначаємо середній квадрат та дисперсію стаціонарного процесу і сигналу:

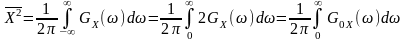; (12.19)

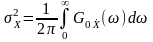. (12.20)

Перехід до циклічної частоти 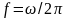замість кругової дає такі співвідношення:

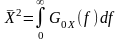; (12.21)

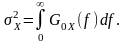(12.22)

Інтеграл від енергетичного спектра в визначених межах для частотної змінної дає значення середньої потужності нецентрованого чи дисперсії центрованого процесу, яке в точності збігається з площею, обмеженою графіком спектра та віссю абсцис у частині інтервалу зміни частоти.

Слід зазначити, що в літературі можливі найрізноманітніші підходи щодо введення одностороннього та двостороннього енергетичних спектрів, пов’язані в основному з урахуванням коефіцієнта пропорційності 2. Останнє серйозно впливає на розмірність.

У нашому випадку розмірність енергетичного спектра [ ]=[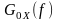 ]=ампл²/Гц.

ПІДСУМКИ
1. Математичний спектр потужності визначається як для додатних, так і від’ємних значень частоти, а фізичний – тільки для додатних частот. 2. У літературі можливі найрізноманітніші підходи щодо введення одностороннього та двостороннього енергетичних спектрів, пов’язані з урахуванням коефіцієнта пропорційності 2. .	3. Рівності, які встановлюють взаємозв’язок одно- та двостороннім спектром потужності: - для нецентрованого випадкового стаціонарного процесу - для центрованого випадкового стаціонарного процесу

Лекція 13. Взаємозв’язок кореляційної функції та спектральної щільності потужності.

Теорема Вінера-Хінчина. Обмеження, що накладаються на АКФ СВП. Додатньо-визначені АКФ. Спектрально-кореляційна структура СВП типу "білий шум". Ширина спектру СВП. Способи визначення ширини спектра. Ефективна ширина спектра. Зв'язок ширини спектра та інтервалу кореляції.

Взаємозв’язок кореляційних та спектральних характеристик стаціонарних процесів