4. Властивості спектральної щільності потужності свп. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп

Відповідно до означення (див. (12.10)) та з урахуванням того, що математичне очікування невід’ємної функції 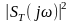є додатним, спектральна щільність потужності є

• функцією дійсною, невід’ємною та парною:

.

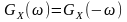• Спектри центрованого та нецентрованого процесів задовольняють такому співвідношенню:

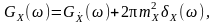(12.15)

де - математичне очікування процесу , а 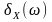- дельтоподібна складова спектральної щільності потужності .

Справедливість співвідношення (12.15) підтверджується відомим результатом інтегрування його правої та лівої частин з одночасним множенням на : середній квадрат дорівнює сумі дисперсії та квадрата математичного очікування.

Формула (12.15) в позначеннях циклічної частоти набуває такого вигляду:

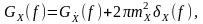
Якщо математичне очікування нецентрованого стаціонарного процесу дорівнює нулю, то спектр та спектр флуктуацій збігаються.

Відмінність від нуля математичного очікування стаціонарного процесу зумовлює в його спектрі дельтоподібну складову.

Тому нецентровані процеси з постійними складовими, характеризуються нераціональними спектрами .

Наведемо обгрунтування цієї властивості з фізичного погляду. Так, постійний процес характеризується нескінченною енергією, але кінцевою середньою потужністю. В частотній області вся така потужність зосереджується тільки на нульовій частоті в межах нульового інтервалу, в якому інші складові відсутні. Тому можна вважати, що потужність кінцевої величини відповідає частотному інтервалу нульової ширини. Останнє еквівалентне нескінченному значенню на частоті 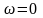, тобто наявності дельта особливості на цій частоті.

Подібна спостерігається у разі, якщо процес або 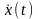містить періодичні складові з частотами . Тоді цим складовим відповідають дельта складові відповідної ваги в спектральній щільності потужності.

Приклад. Обчислити середню потужність процесу, спектр якого є рівномірним у смузі частот від 90 до 110 кГц та набуває значення 2 10^-3 В²/Гц.

Оскільки в спектрі відсутності дельта-особливості, то маємо центрований процес, для якого середня потужність всього процесу збігається з потужністю (дисперсією) його флуктуацій:

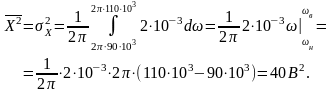
►Приклад. Стаціонарний випадковий процес характеризується спектральною щільністю потужності

.

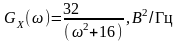Середня потужність сигналу, що розсіюється на резисторі з опором в 1 Ом

.

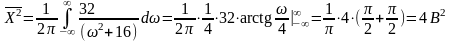ПІДСУМКИ

1.Наявність у спектрі нецентрованого стаціонарного випадкового процесу дельтоподібної складової спричинена ненульовим значенням математичного очікування. 2. Якщо математичне очікування нецентрованого стаціонарного процесу дорівнює нулю, то його спектр потужності та спектр потужності флуктуацій збігаються. 3. Характер спектра потужності залежить від середовища, в якому відбувається процес (електричне коло, механічна система, напівпровідник тощо).

4. Спектр потужності стаціонарного випадкового процесу є функцією дійсною, невід’ємною та парною. 5. Рівність, яка встановлює взаємозв’язок спектрів центрованого та нецентрованого стаціонарних процесів: .
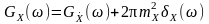