
- •1.Закони розподілу випадкових процесів процесів
- •2. Одновимірні інтегральний та диференціальний закони розподілу
- •Неперервного (а), дискретного (б) та змішаного (в) процесів.
- •Закони розподілу ймовірностей дискретного процесу.
- •Щільності (б) ймовірностей дискретного процесу.
- •1 Загальна характеристика моментних функцій
- •2.Порядок та розмірність момент них функцій
- •3.Початкові моментні функції. Структура формул
- •4 Одновимірні моментні функції першого порядку
- •1.Одновимірні моментні функції другого порядку
- •Очікуваннями і різними дисперсіями.
- •Процесів із однаковими математичними очікуваннями
- •Початковою фазою: а – реалізації випадкового процесу;
- •1.Обчислення одновимірних моментних функцій за характеристичними.
- •2. Поновлення одновимірних характеристичних функцій за моментними.
- •6.1 Види статистичної залежності
- •Кореляцією (б) та некорельовані величини (в).
- •6.2 Двовимірні моментні функції другого порядку
- •7.1 Вкф двох випадкових процесів
- •Його кореляційна функція (б).
- •7.2 Нормовані кореляційні функції.
- •7.3 Особливості кореляційних характеристик
- •1 Визначення стаціонарності у вузькому та широкому значеннях
- •8.2 Математичне очікування,середній квадрат,дисперсія свп
- •8.3 Властивості акф нецентрованого та центрованого свп
- •Процесу (а) та похідної від нього (б).
- •Випадкового процесу.
- •3.Практичне застосування вкф для вирішення проблем виділення слабкого сигналу з суміші.
- •1. Визначення ергодичних випадкових процесів
- •2. Достатні умови ергодичності свп. Умова Слуцького
- •Спектральні характеристики випадкових процесів
- •1. Постановка задачі спектрального аналізу вп
- •2. Енергетичний спектр нестаціонарного вп та його зв'язок з кореляційною функцією.
- •3.Спектральна щільність потужності свп та її фізичний зміст. Спектр флуктуацій (центрованого) свп. Середній квадрат (дисперсія) та спектр свп.
- •4. Властивості спектральної щільності потужності свп. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп
- •5. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп
- •1. Теорема Вінера-Хінчина. Обмеження, що накладаються на акф свп. Додатньо-визначені акф.
- •1.Постановка задачі кореляційного аналізу лінійних систем при дії свп
- •3.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
- •4.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
- •5.Автокореляційна функція реакції. Згортка акф дії та імпульсної характеристики.
- •6. Кореляція процесів на вході та виході лінійної системи. Оцінка статистичного зв'язку "білого шуму" та реакції на нього лінійної системи.
- •З урахуванням властивості дзеркальної симетрії
- •Дійсно,
- •1.Аналіз у частотній області.
- •4. Спектральний аналіз інтегруючої системи при дії "білого шуму".
- •5. Енергетичний спектр реакції ідеального диференціатора.
- •На нього ідеального диференціатора (б).
2. Енергетичний спектр нестаціонарного вп та його зв'язок з кореляційною функцією.
Розглянемо нестаціонарний процес з обмеженою енергією та спектральною щільністю амплітуд , визначеною відповідно до (12.4). У цьому разі, як відмічалось, є випадковою функцією , а її кожна реалізація відповідає певній реалізації процесу .
Згідно з теоремою Парсеваля для окремої реалізації її енергія
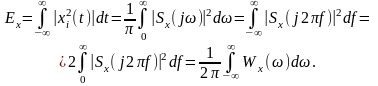 (12.5)
(12.5)
Виходячи
з визначення інтегралу як суми, величина
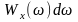 є енергією
є енергією
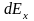 спектральної складової реалізації
процесу
,
що відповідає смузі частот
.
спектральної складової реалізації
процесу
,
що відповідає смузі частот
.
Як
випливає з (12.5) функція
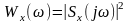
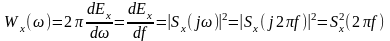
характеризує розподіл енергії реалізації по осі частот і називається спектральною щільністю енергії реалізації або просто її енергетичним спектром.
Розмірність енергетичного спектра реалізації - [енергія/Гц].
Застосовуючи операцію усереднення до ансамблю енергетичних спектрів усіх реалізацій, отримаємо енергетичний спектр нестаціонарного випадкового процесу :
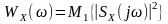 .
(12.6)
.
(12.6)
Ураховуючи
те, квадрат модуля
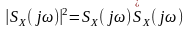 ,
де
,
де
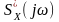 -
комплексно-спряжена до
функція,
а також
(12.4).
дістанемо:
-
комплексно-спряжена до
функція,
а також
(12.4).
дістанемо:
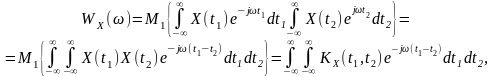 (12.7)
(12.7)
де
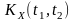 - кореляційна
функція
нестаціонарного
процесу
.
- кореляційна
функція
нестаціонарного
процесу
.
Основні
властивості спектральної щільності
енергії. Відповідно
до означення (12.6) спектральна щільність
енергії
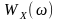 :
:
є невід’ємною (
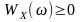 )
і парною відносно частоти;
)
і парною відносно частоти;
не несе інформації про фазові співвідношення спектральних складових;
є функцією невипадковою та дійсною.
ПІДСУМКИ |
|
1.Парність спектральної щільності енергії дає змогу оцінювати спектральний розподіл енергії процесу тільки за тими його значеннями, що обчислені для додатних значень частоти. 2. Відсутність же у спектрі енергії нестаціонарного процесу його фазових параметрів є причиною неоднозначного поновлення випадкового процесу за його спектром: один і той самий енергетичний спектр може визначати декілька процесів, зокрема, зсунутих у часі. |
3.Енергетичний спектр нестаціонарного випадкового процесу =
= |
3.Спектральна щільність потужності свп та її фізичний зміст. Спектр флуктуацій (центрованого) свп. Середній квадрат (дисперсія) та спектр свп.
Застосовувати
перетворення Фур'є безпосередньо до
стаціонарного процесу
,
кожна реалізація якого з ймовірністю
одиниця характеризується нескінченною
енергією, неможливо. Для того, щоб це
перетворення існувало, слід розглянути
не весь процес
,
а його обмежену частину
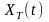 ,
визначену на кінцевому часовому інтервалі
,
визначену на кінцевому часовому інтервалі
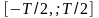 :
:
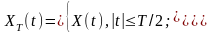 (12.8)
(12.8)
Такий
обмеженої тривалості процес
має кінцеву енергію і для нього існує
як перетворення Фур’є
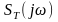 ,
так і спектральна щільність енергії
,
так і спектральна щільність енергії
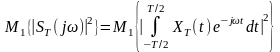 .
.
Проте
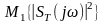 є функцією не тільки частоти, а і часового
інтервалу
.
Тому доцільно розглядати нормовану
відносно Т
спектральну енергетичну характеристику
є функцією не тільки частоти, а і часового
інтервалу
.
Тому доцільно розглядати нормовану
відносно Т
спектральну енергетичну характеристику
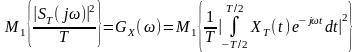 .
(12.9)
.
(12.9)
Відношення
енергії до часу визначає потужність.
Ось чому
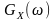 називається
спектральною
щільністю
потужності процесу
називається
спектральною
щільністю
потужності процесу
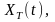 обмеженої
тривалості.
Спрямувавши
та врахувавши,
що
у цьому
разі
обмеженої
тривалості.
Спрямувавши
та врахувавши,
що
у цьому
разі
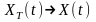 ,
дістанемо співвідношення для визначення
спектральної
щільності потужності
стаціонарного
процессу
:
,
дістанемо співвідношення для визначення
спектральної
щільності потужності
стаціонарного
процессу
:
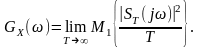 (12.10)
(12.10)
Спектральну щільність потужності стаціонарного випадкового процесу ще називають енергетичним спектром або спектром потужності.
Отже,спектр потужності відображає розподіл потужності стаціонарного процесу по частотному діапазону і не несе в собі інформації про його фазові параметри.
Обчислимо
інтеграл
від лівої
і правої
частин
(12.10)
в межах
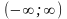 :
:
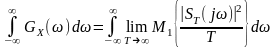 .
.
Міняючи місцями операції граничного переходу та інтегрування, а також враховуючи, що математичне очікування від інтегралу дає інтеграл математичного очікування, отримаємо:
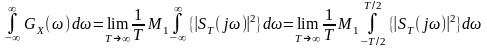 .
.
Поділимо
ліву і праву частину останнього
співвідношення на
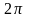 та враховуємо теорему Парсеваля. Тоді
та враховуємо теорему Парсеваля. Тоді
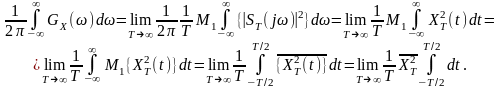
Ураховуючи те, що при процес обмеженої тривалості , для стаціонарного випадкового процесу дістанемо:
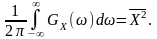 (12.11)
(12.11)
Відомо,
що середній квадрат випадкового процесу
визначає його середню потужність, тому
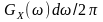 є тією частиною повної потужності, якою
наділена спектральна складова з частотою
із частотного діапазону [
,
є тією частиною повної потужності, якою
наділена спектральна складова з частотою
із частотного діапазону [
,
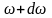 ].
].
Тоді
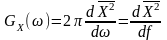 .
(12.12)
.
(12.12)
Спектральна щільність потужності стаціонарного випадкового процесу відображає розподіл його потужності по частотному діапазону і для конкретного значення частоти визначає потужність певної спектральної складової.
У цьому і є фізичний зміст енергетичного спектра .
Розмірність спектральної щільності потужності безпосередньо випливає з (12.12): =амплітуда2/Гц = амплітуда2 .с.
Співвідношення (12.11) дає змогу зробити ще і такий висновок:
графік спектральної щільності потужності та вісь абсцис обмежують площу, яка за значенням перевищує потужність нецентрованого випадкового стаціонарного процесу в 2 разів.
Спектральна щільность потужності центрованого випадкового стаціонарного процесу :
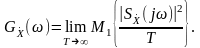
У цьому разі
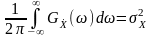 ;
(12.13)
;
(12.13)
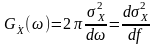 .
(12.14)
.
(12.14)
Згідно
з (12.13)
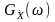 часто називають
спектральною
щільністю
дисперсії.
часто називають
спектральною
щільністю
дисперсії.
ПІДСУМКИ |
|
1. Для певного значення частоти спектральна щільність потужності стаціонарного випадкового процесу подає потужність певної спектральної складової. 2. Може існувати декілька періодичних процесів і сигналів із одного і того самого періоду, які мають однакову автокореляційну функцію. 3. Спектр АКФ дає інформацію про розподіл потужностей гармонік періодичного процесу і сигналу по частоті. Такий розподіл можна отримати і на основі процесу (сигналу) за теоремою Парсеваля.
|
4. Спектр потужності відображає розподіл потужності стаціонарного процесу по частотному діапазону і не несе в собі інформації про його фазові параметри. 5. Розмірність спектральної щільності потужності: амплітуда2/Гц = амплітуда2 .с. 6. Формули: - спектр потужності нецентрованого стаціонарного процесу;
зв’язок спектра потужності нецентрованого стаціонарного процесу з середнім квадратом; - взаємо-зв’язок спектра потужності центрованого стаціонарного процесу з диперсією; - спектр потужності центрованого стаціонарного випадкового процесу. |

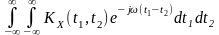 .
.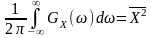 -
взаємо-
-
взаємо-