Спектральні характеристики випадкових процесів

1. Постановка задачі спектрального аналізу вп

Під час теоретичного дослідження різних перетворень детермінованих процесів лінійними системами для їх спектрального зображення, як відомо, широко застосовується перетворення Фур’є, що дає змогу істотно спростити процедуру аналізу за рахунок переходу від операції згортки у часовій області до звичайної операції множення відповідних характеристик систем та процесів у частотній області. В зв’язку з цим виникає природне запитання: чи є ці методи раціональними під час дії на систему випадкових процесів?

Перетворенням Фур’є детермінованого неперіодичного процесу 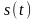є комплексна функція частоти 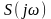або 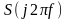, яка визначається за такою формулою:

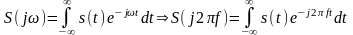(12.1)

Функцію 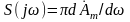називають спектральною щільністю комплексних амплітуд детермінованого процесу. Така функція визначає комплексну амплітуду гармонічної складової з частотою в інтервалі 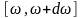, сума яких відтворює початковий процес .

Застосування прямого перетворення Фур’є до випадкових процесів стикається з рядом проблем.

Проблема перша. Інтеграл (12.1) існує, коли підінтегральна функція є абсолютно інтегровною, що забезпечується за абсолютної збіжності інтегралу

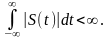(12.2)

Практично достатньо, щоб функція була інтегровною в квадраті:

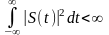(12.3)

Інтеграл (12.3) визначає енергію процесу. Отже, перетворення Фур'є існує для процесів із обмеженою енергією. Водночас, наприклад, для ергодичного процесу кожна його вибіркова функція (реалізація) з ймовірностю одиниця характеризується нескінченною енергією, оскільки є заданою на нескінченному відрізку часу. Основною енергетичною характеристикою такого процесу, як відомо, є середня потужність, що дорівнює його середньому квадрату.

Отже, використання для оцінки властивостей стаціонарних випадкових процесів спектральної щільності амплітуд виду (12.1), що пов’язана з поняттям енергії, неможливо. Слід, виходити з такої енергетичної характеристики, як потужність.

Проблема друга. Для нестаціонарного випадкового процесу або , тобто процесу, кожна реалізація якого характеризується в загальному випадку обмеженою енергією, можливе застосування перетворення Фур'є, але з результатом у вигляді випадкової комплексної функції частоти:

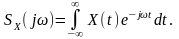(12.4)

Проте, як показують теоретичні дослідження, функція 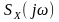характеризує більше не ансамбль реалізацій у цілому, а кожну реалізацію окремо, оскільки певна реалізація функції є індивідуальною характеристикою реалізації процесу .

Головне ж, як відмічалось, полягає у тому, що функція є випадковою. Бажано ж мати таке визначення спектра, яке привело б нас до невипадкової функції частоти.

Ось чому спектральний опис випадкових процесів і сигналів проводять на основі функцій, які визначають розподіл не амплітуд спектральних складових процесу, а їхньої енергії по частотному діапазону.

ПІДСУМКИ
1. Для оцінки спектральних властивостей стаціонарних випадкових процесів потрібно застосовувати характеристики, що ґрунтуються на понятті потужності.	2. Спектральний опис випадкових процесів проводять на основі функцій, які визначають розподіл не амплітуд спектральних складових процесу, а їхньої енергії по частотному діапазону.