1. Визначення ергодичних випадкових процесів
Розглянемо
одну довільну реалізацію
стаціонарного випадкового процесу
(рис.11.1) на нескінченно довгому інтервалі
часу
.
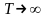В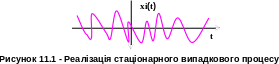
изначимо
середнє
значення цієї однієї реалізації за час
T
усередненням у
часі за відомою формулою:
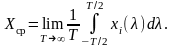
Відомо,
що
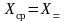називають постійною складовою реалізації
.
Аналогічно,
-
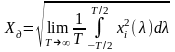середньоквадратичне значення реалізації
нецентрованого процесу та
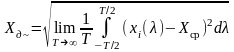
- середньоквадратичне значення змінної складової реалізації або реалізації центрованого процесу.
Квадрат середньоквадратичного значення змінної складової реалізації
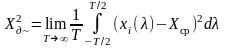
є
величиною, пропорційною середній
потужності цієї складової, а потужність
постійної складової - квадрату
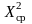середнього значення.
Повна
потужність реалізації в цілому:
.
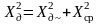Тепер
припустімо, що середнє значення
випадкового процесу
(його
математичне очікування)
,
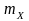отримане усередненням по всім реалізаціям,
збігається з середнім значенням
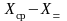його окремої реалізації
;
середній квадрат
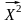– з квадратом її середньоквадратичного
значення
,
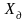а дисперсія
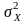– з квадратом середньоквадратичного
значення її змінної складової. За таких
умов
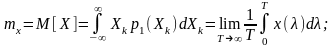
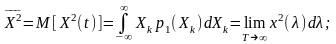
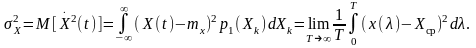
Стаціонарні випадкові процеси, для яких усереднення по ансамблю (по всім реалізаціям) дає такий самий результат як усереднення в часі за однією реалізацією нескінченної тривалості, називають ергодичними.
2. Достатні умови ергодичності свп. Умова Слуцького
Еквівалентність операцій усереднення повинна виконуватись під час обчислення всіх можливих статистичних характеристик. Ось чому процес буде ергодичним перш за все тільки тоді, коли, він є стаціонарним у широкому значенні. Це є необхідною умовою.
Достатньою
умовою ергодичності
випадкового стаціонарного процесу є
прямування до нуля границі АКФ, коли її
аргумент
:
.
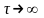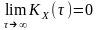Слабкішою є вимога, що має назву умови Слуцького:
.
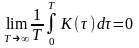Стаціонарний випадковий процес може бути ергодичним не тільки відносно своїх моментних функцій, а й відносно скінченновимірних функцій розподілу.
Необхідною
та достатньою умовою ергодичності
стаціонарного у вузькому розумінні
випадкового процесу
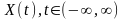відносно
одновимірної функції розподілу
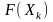є
така:
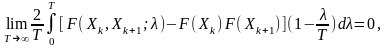
де
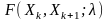- двовимірна функція розподілу процесу
.
3. Кореляційні характеристики ергодичних СВП
Функція автокореляції ергодичного процесу:
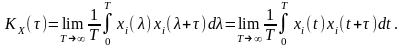
Для ергодичних процесів і функція взаємної кореляції
.
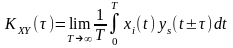Аналогічні співвідношення можна записати і для центрованих ергодичних процесів.
Таким чином, для ергодичного процесу одна реалізація достатньо великої тривалості є типовим представником статистичного ансамблю в цілому. Вивчаючи таку одну реалізацію, ми можемо достатньо точно охарактеризувати відповідний стаціонарний випадковий процес. Такий підхід лежить в основі практично всіх підходів експериментального визначення статистичних характеристик випадкових процесів.
Приклад.
На
вході системи із N однотипних безінерційних
підсилювачів діють сигнали, що є
реалізаціями стаціонарного процесу
Х(t)
, середнє значення якого
.
Коефіцієнти передачі підсилювачів
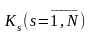є випадковими величинами з дисперсією
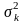та математичним очікуванням
.
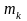Порівняти середнє значення, дисперсію
та функцію кореляції вихідного випадкового
процесу підсилювачів, розраховані
усередненням по всім реалізаціям та
одій із них.
Сукупність
реалізацій на виході всіх підсилювачів
утворює випадковий процес
,
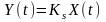кожна реалізація якого
.
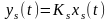На виході s–го підсилювача середнє значення реалізації
;
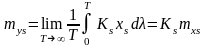дисперсія
;
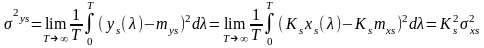функція кореляції центрованого процесу
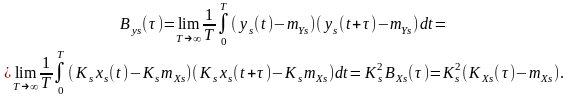
Все це статистичні характеристики розраховані за однією реалізацією. Тепер визначимо відповідні характеристики за ансамблем реалізацій.
Середне значення (математичне очікування) з урахуванням того, що випадкова величина K та процес X(t) є статистично незалежними
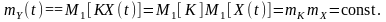
Отже,
математичне очікування вихідного
процесу є величиною сталою.
Зрозуміло, що середнє статистичне за
однією реалізацією та ансаблем не
збігаються:
.
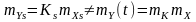Функція
автокореляції центрованого вихідного
процесу
,
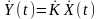який є, як і вхідний процес, стаціонарним
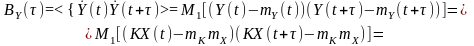
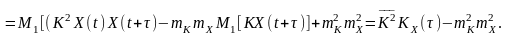
Дисперсію процесу Y(t) обчислимо як початкове значення кореляційної функції:
.
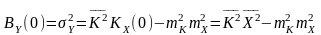Результати обчислень за ансамблем реалізацій та одній із них не збігаються. Отже, процес Y(t) не є ергодичним. Це є наслідком того, що, незважаючи на стаціонарність Y(t), жодна з реалізацій не є представницькою.
ПІДСУМКИ |
|
1. Випадковий процес буде ергодичним перш за все тільки тоді, коли він є стаціонарним у широкому значенні. 2. Для ергодичного процесу одна реалізація достатньо великої тривалості є типовим представником статистичного ансамблю в цілому. 3. Експериментальне визначення статистичних характеристик випадкових процесів грунтується на розгляді процесів як ергодичних. |
.
|
4. Умова Слуцького:
.
Лекція 12. Спектр стаціонарних випадкових процесів.
Постановка задачі спектрального аналізу ВП. Енергетичний спектр нестаціонарного ВП та його зв'язок з кореляційною функцією. Спектральна щільність потужності СВП та її фізичний зміст. Спектр флуктуацій (центрованого) СВП. Середній квадрат (дисперсія) та спектр СВП. Властивості спектральної щільності потужності СВП. Спектр монохроматичного СВП. Односторонній та двохсторонній, фізичний та математичний спектри СВП.