
- •1.Закони розподілу випадкових процесів процесів
- •2. Одновимірні інтегральний та диференціальний закони розподілу
- •Неперервного (а), дискретного (б) та змішаного (в) процесів.
- •Закони розподілу ймовірностей дискретного процесу.
- •Щільності (б) ймовірностей дискретного процесу.
- •1 Загальна характеристика моментних функцій
- •2.Порядок та розмірність момент них функцій
- •3.Початкові моментні функції. Структура формул
- •4 Одновимірні моментні функції першого порядку
- •1.Одновимірні моментні функції другого порядку
- •Очікуваннями і різними дисперсіями.
- •Процесів із однаковими математичними очікуваннями
- •Початковою фазою: а – реалізації випадкового процесу;
- •1.Обчислення одновимірних моментних функцій за характеристичними.
- •2. Поновлення одновимірних характеристичних функцій за моментними.
- •6.1 Види статистичної залежності
- •Кореляцією (б) та некорельовані величини (в).
- •6.2 Двовимірні моментні функції другого порядку
- •7.1 Вкф двох випадкових процесів
- •Його кореляційна функція (б).
- •7.2 Нормовані кореляційні функції.
- •7.3 Особливості кореляційних характеристик
- •1 Визначення стаціонарності у вузькому та широкому значеннях
- •8.2 Математичне очікування,середній квадрат,дисперсія свп
- •8.3 Властивості акф нецентрованого та центрованого свп
- •Процесу (а) та похідної від нього (б).
- •Випадкового процесу.
- •3.Практичне застосування вкф для вирішення проблем виділення слабкого сигналу з суміші.
- •1. Визначення ергодичних випадкових процесів
- •2. Достатні умови ергодичності свп. Умова Слуцького
- •Спектральні характеристики випадкових процесів
- •1. Постановка задачі спектрального аналізу вп
- •2. Енергетичний спектр нестаціонарного вп та його зв'язок з кореляційною функцією.
- •3.Спектральна щільність потужності свп та її фізичний зміст. Спектр флуктуацій (центрованого) свп. Середній квадрат (дисперсія) та спектр свп.
- •4. Властивості спектральної щільності потужності свп. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп
- •5. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп
- •1. Теорема Вінера-Хінчина. Обмеження, що накладаються на акф свп. Додатньо-визначені акф.
- •1.Постановка задачі кореляційного аналізу лінійних систем при дії свп
- •3.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
- •4.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
- •5.Автокореляційна функція реакції. Згортка акф дії та імпульсної характеристики.
- •6. Кореляція процесів на вході та виході лінійної системи. Оцінка статистичного зв'язку "білого шуму" та реакції на нього лінійної системи.
- •З урахуванням властивості дзеркальної симетрії
- •Дійсно,
- •1.Аналіз у частотній області.
- •4. Спектральний аналіз інтегруючої системи при дії "білого шуму".
- •5. Енергетичний спектр реакції ідеального диференціатора.
- •На нього ідеального диференціатора (б).
Неперервного (а), дискретного (б) та змішаного (в) процесів.
Згідно з останньою властивістю для неперервної випадкової величини X(tk) закон розподілу F1(Xk, tk) описується неперервною, неспадною без стрибків функцією (рис. 2.3, а).
Для
дискретної випадкової величини функція
розподілу F1(Xk,
tk)
виражається через суму одиничних
ступінчастих функцій
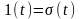 з ваговими коефіцієнтами Pi
(рис. 2.3, б),
кожний з яких є ймовірністю того, що
випадкова величина X(tk)
в
перерізі tk
набуде значення Xi
:
з ваговими коефіцієнтами Pi
(рис. 2.3, б),
кожний з яких є ймовірністю того, що
випадкова величина X(tk)
в
перерізі tk
набуде значення Xi
:
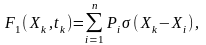
де
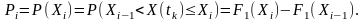 Графічно
Графічно
 - висота сходинки функції розподілу
ймовірностей, що відповідає значенню
Xi.
- висота сходинки функції розподілу
ймовірностей, що відповідає значенню
Xi.
Змішаний випадковий процес характеризується комбінацією неперервних і дискретних величин, а отже, неперервних та стрибкоподібних ділянок на графічному зображенні функції розподілу ймовірностей (рис. 2.3, в).
►Приклад. Одновимірна функція розподілу випадкового процесу
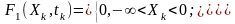
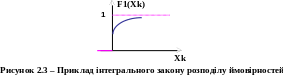
Графічне зображення подано на рис. 2.3Визначити ймовірність того, що
а)
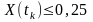 ;
б)
;
б)
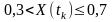 ;
в)
;
в)
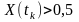 .
.
Задана функція F1(Xk, tk) задовольняє всім властивостям інтегрального закону розподілу ймовірностей.
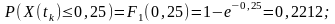
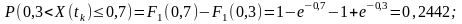
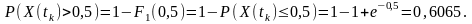
◙П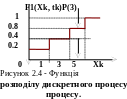 риклад.
Дискретний
випадковий процес характеризується
F1(Xk,
tk),
що зображена на рис.
2.4 Обчислити:
а)
ймовірність
того, що X(tk)
риклад.
Дискретний
випадковий процес характеризується
F1(Xk,
tk),
що зображена на рис.
2.4 Обчислити:
а)
ймовірність
того, що X(tk)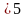 ;
б)
сумарну
ймовірність значень 0,
1, 3, 5;
в)
ймовірність того, що
;
б)
сумарну
ймовірність значень 0,
1, 3, 5;
в)
ймовірність того, що
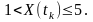
Ймовірність
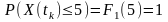 (береться верхнє значення функції
розподілу).
(береться верхнє значення функції
розподілу).
Сумарна ймовірність значень 0, 1, 3, 5 є такою:
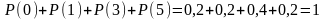 .
.
Ймовірність приналежності до зазначеного інтервалу:
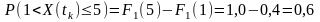 .
.
Математична модель функції розподілу ймовірностей:
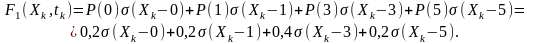
◙
Диференціальний закон розподілу ймовірностей, або функція щільності ймовірностей характеризує швидкість зміни функції розподілу.
Для
перерізу в точці tk
одновимірна
функція щільності ймовірностей
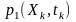 випадкової величини X(tk)
визначається як границя відношення
ймовірності приналежності її значень
до інтервалу
випадкової величини X(tk)
визначається як границя відношення
ймовірності приналежності її значень
до інтервалу
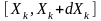 до довжини цього інтервалу
до довжини цього інтервалу
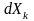 за умови, що його довжина
за умови, що його довжина
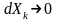 :
:
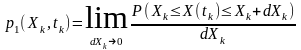 .
(2.2)
.
(2.2)
Розмірність
одновимірної функції щільності
ймовірностей є оберненою до розмірності
величини
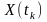 .
.
Згідно
з визначенням ймовірность того, що всі
реалізації випадкового процесу в момент
часу
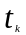 набудуть значень, які лежать в інтервалі
(рис. 2.5), дорівнює
набудуть значень, які лежать в інтервалі
(рис. 2.5), дорівнює
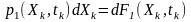 .
Така ймовірність називається елементом
ймовірності.
.
Така ймовірність називається елементом
ймовірності.
Це дозволяє записати диференціальний закон розподілу у вигляді:
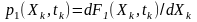 .
(2.3)
.
(2.3)
Згідно з (2.3) дістанемо зв’язок між одновимірними інтегральним та диференціальним законами розподілу ймовірностей в інтегральній формі:
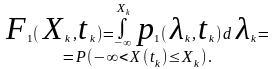 (2.4)
(2.4)
Ф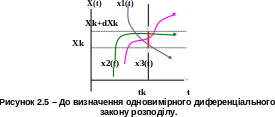 ормули
(2.3) та (2.4) пояснюють походження назв
диференціального та інтегрального
законів.
ормули
(2.3) та (2.4) пояснюють походження назв
диференціального та інтегрального
законів.
Відомі наступні властивості одновимірної щільності ймовірностей:
невід’ємність (додатня визначеність):
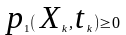 .
.
Оскільки
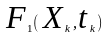 є неспадаючою, то згідно з (2.3)
;
є неспадаючою, то згідно з (2.3)
;
нормованість:
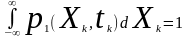 .
(2.5)
.
(2.5)
Співвідношення
(2.5) називають умовою
нормування,
яка відображає той факт, що які б значення
не набувала величина
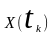 ,
вони завжди будуть в межах інтервалу
,
вони завжди будуть в межах інтервалу
 .
.
Виходячи
із геометричного значення визначеного
інтегралу, відповідно до (2.4) ймовірність
попадання значень випадкового процесу
в одному перерізі в інтервал
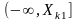 дорівнює площі, обмеженій зверху графіком
одновимірної функції щільності
ймовірностей, а знизу відрізком
осі абсцис (рис.2.6). За умовою нормування
площа, обмежена графіком одновимірної
функції щільності ймовірностей і віссю
абсцис, дорівнює одиниці.
дорівнює площі, обмеженій зверху графіком
одновимірної функції щільності
ймовірностей, а знизу відрізком
осі абсцис (рис.2.6). За умовою нормування
площа, обмежена графіком одновимірної
функції щільності ймовірностей і віссю
абсцис, дорівнює одиниці.
У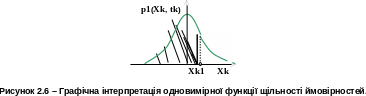 практичних застосуваннях дуже корисне
і таке співвідношення:
практичних застосуваннях дуже корисне
і таке співвідношення:
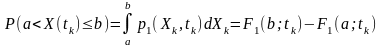 .
(2.6)
.
(2.6)
Ймовірність того, що значення процесу Х(t) в перерізі tk будуть знаходитися в інтервалі (a,b] дорівнює різниці значень функції розподілу на кінцях цього інтервалу.
Геометрично - це площа, обмежена на інтервалі (a, b] графіком одновимірного диференціального закону та відрізком (a, b]) осі абсцис (інтервалом
Приклад. Визначити відношення між константами
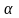 та
та
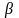 для функції
для функції
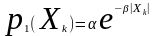 ,
яка
описує
закон
розподілу Лапласа.
,
яка
описує
закон
розподілу Лапласа.
Згідно з умовою нормування
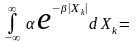
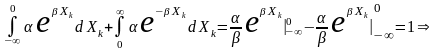
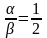 .
.
◙
Нормальний закон закон розподілу ймовірностей
Одновимірна функція щільності ймовірностей для нормального закону
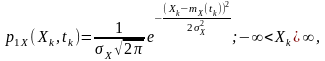 (2.7)
(2.7)
де
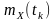 -
математичне очікування або
середньостатистичне значення;
-
математичне очікування або
середньостатистичне значення;
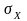 - середньоквадратичне відхиленя
(стандартне відхилення).
- середньоквадратичне відхиленя
(стандартне відхилення).
Графік нормальної функції щільності ймовірностей подано на рис.2.7, а.
Основні його особливості:
Має дзвонову форму з одним максимумом, що відповідає математичному очікуванню .
Графік є симетричним відносно вертикальної прямої, що проходить через точку на осі абсцис, яка визначається значенням математичного очікування.
Максимальне значення функції обернено, а її ширина прямо пропорційна середньоквадратичному значенню .
На рівні 0,607 функція має ширину
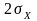 .
Для відповідних цьому
рівню значень
аргументу абсолютне значення похідної
.
Для відповідних цьому
рівню значень
аргументу абсолютне значення похідної
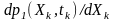 досягає максимуму.
досягає максимуму.
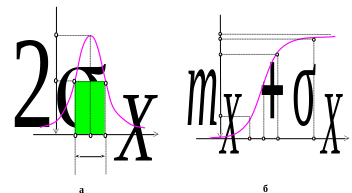
Рисунок 2.7 – Диференціальний (а) та інтегральний (б) нормальний
закон розподілу ймовірностей.
Функція
розподілу ймовірностей
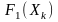 для
нормального
закону (див.
рис. 2.7б)
не
може бути записана компактно через
елементарні. Для обчислення її значень
використовують табульовані
функції.
Слід звернути увагу, що єдності в цьому
питанні немає. Розглянемо різні підходи.
для
нормального
закону (див.
рис. 2.7б)
не
може бути записана компактно через
елементарні. Для обчислення її значень
використовують табульовані
функції.
Слід звернути увагу, що єдності в цьому
питанні немає. Розглянемо різні підходи.
На основі табульованого інтервалу виду
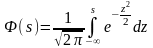 (2.8)
(2.8)
функція розподілу
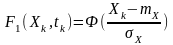 .
(2.9)
.
(2.9)
Інтеграл
(2.8) за формою в точності збігається з
функцією розподілу нормованого
гауссового закону
розподілу, для якого математичне
очікування
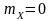 ,
а дисперсія
,
а дисперсія
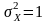 .
Такі параметри є характерними для
центрованих гауссових випадкових
процесів. Ось чому (2.8) називають ще
нормованою
функцією розподілу
або інтегралом
ймовірностей.
.
Такі параметри є характерними для
центрованих гауссових випадкових
процесів. Ось чому (2.8) називають ще
нормованою
функцією розподілу
або інтегралом
ймовірностей.
Значення
інтегралу ймовірностей
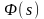 подаються
в таблицях, як правило, для невід’ємних
значень аргументу s.
Тому часто є корисним додаткове
співвідношення:
подаються
в таблицях, як правило, для невід’ємних
значень аргументу s.
Тому часто є корисним додаткове
співвідношення:
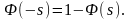 (2.10)
(2.10)
Деякі
автори для інтеграла ймовірностей
використовують позначення
виду
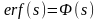 і називають його функцією
похибок.
і називають його функцією
похибок.
Однак інші автори визначають функцію похибок так:
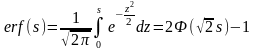 (2.11)
(2.11)
і також називають її функцією Лапласа або інтегралом похибок чи інтегралом ймовірностей похибок.
Для нормального закону справедливими та важливими з практичного погляду є висновки, які ми наводимо без доведення.
Випадкова величина із нормальним законом розподілу ймовірностей повністю характеризується математичним очікуванням та середньоквадратичним відхиленням
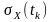 .
.
Випадкова величина
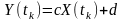 ,
де
,
де
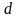 і
і
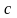 - дійсні константи, а
- нормально розподілена випадкова
величина, має нормальний законом
розподілу.
- дійсні константи, а
- нормально розподілена випадкова
величина, має нормальний законом
розподілу.
Інакше кажучи, нормальний розподіл інваріантний відносно зазначених лінійних перетворень.
Сума
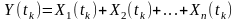 незалежних випадкових величин
незалежних випадкових величин
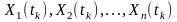 має нормальний розподіл у разі, якщо
всі вони нормально розподілені. Тоді
математичне очікування
має нормальний розподіл у разі, якщо
всі вони нормально розподілені. Тоді
математичне очікування
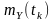 та середньоквадратичне відхилення
та середньоквадратичне відхилення
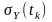 величини
величини
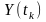 задовольняють такі співвідношення:
задовольняють такі співвідношення:
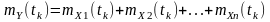 ;
;
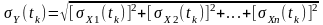 .
.
Виходячи з того, що багато реальних явищ, які носять випадковий характер, є результатом суперпозиції окремих подій, відповідно до центральної граничної теореми, незалежно від виду функції щільності ймовірностей окремих складових (а дуже часто вони невідомі), можливо очікувати, що функція щільності ймовірностей сумарного процесу буде нормальною.
Приклад. Визначити ймовірність того, що в перерізі відхилення миттєвих значень процесу Х(t) з нормальним законом ліворуч і праворуч від середнього не перевищать
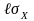 .
.
За означенням ймовірность потрапляння у вказаний інтервал
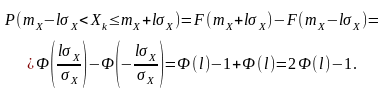
Якщо
врахувати, що для
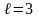 значення
інтегралу ймовірності Ф(3)=0,99865, то
значення
інтегралу ймовірності Ф(3)=0,99865, то
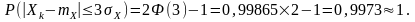
Ймовірність відхилення миттєвих значень випадкового процесу з нормальним законом розподілу від математичного очікування ліворуч і праворуч на
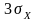 приблизно дорівнює одиниці.
приблизно дорівнює одиниці.
Іншими
словами, випадковий процес із нормальним
законом розподілу в перерізі
малоймовірно може відхилятися від
на величину, що перевищує
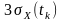 .
У літературі цей висновок називають
“правилом
трьох сигм”.
.
У літературі цей висновок називають
“правилом
трьох сигм”.
◙
Застосування ступінчатих функцій для опису законів розподілу
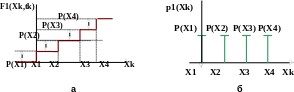 ◙
◙
Рисунок 2.8- Інтегральний (а) та диференціальний (б)
