3.Практичне застосування вкф для вирішення проблем виділення слабкого сигналу з суміші.

Застосування взаємних кореляційних функцій для розв’язання завдань перетворення інформації пов’язано з системами, на входах яких діє два і більше випадкових процесів чи сигналів.

Розглянемо випадковий процес , що є адитивною сумішшю корисного процесу та шуму . Припустімо, що та є стаціонарними та незалежними. Тоді для центрованого процесу 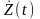функція кореляції

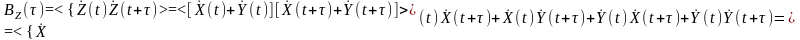
Отже, автокореляційна функція адитивної суміші стаціонарних випадкових процесів дорівнює алгебраїчній сумі АКФ процесів-складових та всіх можливих їхніх взаємних кореляційних функцій.

Виходячи з статистичної незалежності, процеси та є і некорельованими, а отже 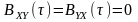. Остаточно

З урахуванням зв’язку між кореляційними функціями нецентрованого та центрованого випадкових процесів АКФ суміші нецентрованих незалежних стаціонарних процесів

.

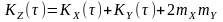Приклад. Розглянемо гармонічний процес , де – випадковий параметр із рівномірним законом розподілу. Такий процес називають монохроматичним стаціонарним випадковим процесом (СВП). Як відомо, функція кореляції такого процесу .

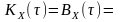
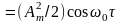Припустімо, що - статистично незалежний від процесу Х(t) шум із нульовим математичним очікуванням 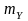= 0 та функцією кореляції 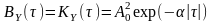. Тоді з урахуванням того, що 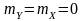, суміш характеризується функцією кореляції

,

графік якої, коли потужність періодичного процесу набагато менше потужності шуму, зображено на рис. 10.1 Із графіка і формули ясно, що для великих значень зсуву між перерізами  АКФ суміші наближається до АКФ корисного сигналу:

.

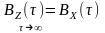Тому при використанні належного методу вимірювання АКФ корисного слабкого процесу, подавленого потужнім шумом , з’являється можливість його виділення з суміші.

Приклад. Ще одним прикладом виділення слабкого, але відомого сигналу із суміші з шумом, пов’язаного з операцією формування взаємної функції кореляції, може слугувати функціонування радіолокаційної системи. Передавач такої системи генерує сигнал . Вхідний сигнал радіолокаційного приймача

д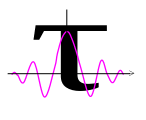 е - час поширення сигналу від передавача до приймача (наприклад, деякої реальної цілі) та в зворотньому напрямку; N(t)- шум приймача; а - стала, яка набагато менше, ніж одиниця.

Зазвичай середня потужність сигналу набагато менша, ніж потужність шуму N(t). Обчислимо функцію взаємної кореляції сигналів X(t) та Y(t), зважаючи на те, що вони є стаціонарно-зв’язаними та з нульовими математичними очікуваннями:

Оскільки сигнали X(t) та N(t) є статистично незалежними, то іхня взаємна кореляційна функція 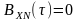. Тоді

.

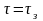Функція набуває максимального значення, яке дорівнює середній потужності процесу X(t), як відомо, за нульового значення її аргументу. Таким чином, визначення відстані до цілі зводиться до знаходження максимуму ВКФ .

ПІДСУМКИ
1. АКФ алгебраїчної суми двох статистично незалежних центрованих стаціонарних процесів визначається алгебраїчною сумою АКФ складових, а для нецентрованих процесів ще і подвоєним добутку їхніх статистичних середніх.	2. Автокореляційна функція адитивної суміші стаціонарних випадкових процесів дорівнює алгебраїчній сумі АКФ процесів-складових та всіх можливих їхніх взаємних кореляційних функцій.

Лекція 11. Ергодичні випадкові процеси.

Визначення ергодичних випадкових процесів. Достатні умови ергодичності

СВП. Умова Слуцького.Кореляційні характеристики ергодичних СВП.