Випадкового процесу.
У
разі, якщо
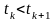(рис. 9.5, б),
пряма ОА
для ненульових пар значень
для інтегралу по
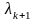визначає такі співвідношення:
;
.
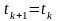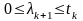Тому тепер кореляційна функція
.
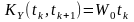Зважаючи на те, що в обох випадках функція кореляції явно залежить від або , а не від різниці, то вінеровський випадковий процес у широкому значенні є нестаціонарним.
Дисперсію
знаходимо на основі визначеної
кореляційної функції
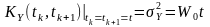для співпадаючих перерізів:
=
=
t.
Вона не є постійною, а лінійно зростає
з часом, що також є ознакою нестаціонарності
зінтегрованого процесу.
ПІДСУМКИ |
|
1. Умовою диференціювання стаціонарного випадкового процесу є існування другої похідної від його автокореляційної функції. 2. Середні значення процесів на вході та виході лінійної системи, властивості якої описуються лінійним операторм , пов’язані тим самим оператором. 3. Інтегральне перетворення стаціонарних процесів дає процес нестаціонарний
|
4. Кореляційна функція здиференційованого процесу визначається із знаком мінус похідною другого порядку від кореляційної функції початкового процесу: 5. Математичне очікування випадкового процесу, що є результатом інтегрування стаціонарного, є функцією часу, а його кореляційна функція залежить як від початку відліку часу, так і відстані між перерізами. |
Лекція 10. Стаціонарно-зв'язані випадкові процеси.
Стаціонарно-зв'язані ВП. Визначення та властивості кореляційних функцый стаціонарно-зв'язаних ВП. Взаємна кореляційна функція СВП та похідної від нього. Практичне застосування ВКФ для вирішення проблем виділення слабкого сигналу з суміші.
1.Стаціонарно-зв'язані ВП. Визначення та властивості кореляційних функцій стаціонарно-зв'язаних ВП.
Розглянемо два випадкових процеси і , кожний з яких окремо задовольняє умовам стаціонарності.
Два стаціонарних процеси є стаціонарно-зв’язанами, якщо для будь-якого n багатовимірні спільні закони розподілу ймовірностей не змінюються під час одночасного довільного зсуву моментів відліку вздовж часової осі на довільний інтервал .
Наприклад, для двовимірних законів розподілу стаціонарно-зв’язані випадкові процеси задовольняють таку умову:
.
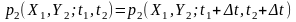2.Взаємна кореляційна функція СВП та похідної від нього.
Як
відомо, мірою статистичного зв’язку
між двома процесами є двовимірна моментна
функція другого порядку: для нецентрованих
і
процесів – це взаємна кореляційна
функція
;
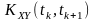для центрованих процесів - функція
взаємної кореляції
.
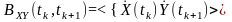За визначенням, зокрема, для неперервних процесів
.
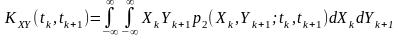Враховуючи властивості стаціонарно-зв’язаних процесів, останнє співвідношення можна записати в такій формі:
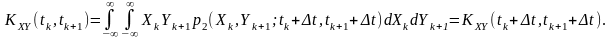
Для
будь-якого
,
зокрема, і
,
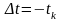дістанемо
.
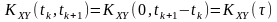Взаємна кореляційна функція стаціонарно-зв’язаних випадкових процесів є функцією тільки зсуву між перерізами і не залежить від початку відліку часу або моментів часу визначення перерізів.
Зважаючи на таку властивість, у формулах для взаємних кореляційних стаціонарно-зв’язаних функцій не записують позначення моментів часу:
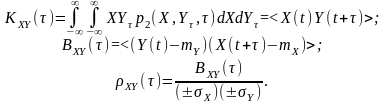
Можна показати, що при зміні порядку слідування індексів
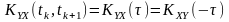
Якщо два процеси є стаціонарними, але не стаціонарно-зв’язаними, то функція взаємної кореляції буде залежати як від початку відліку часу , так і часового інтервалу .
Функції взаємної кореляції незалежно від виду процесу не задовольняють умову симетрії відносно слідування процесів (порядку слідування нижніх індексів):
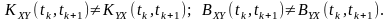
У разі, якщо процеси є стаціонарно-зв’язаними, то існує особливий вид симетрії відносно аргументу (властивість дзеркального відображення), що подається такими співвідношеннями:
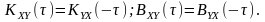
Дійсно, за визначенням
.
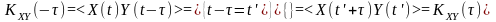На відміну від функцій автокореляції максимальне значення функції взаємної кореляції стаціонарно-зв’язаних випадкових процесів не обов’язково відповідає співпадаючим у часі перерізам, тобто коли =0. Такий максимум може бути за будь-якого значення . Проте
для стаціонарно-зв’язаних процесів миттєве значення їхньої взаємної кореляційної функції не перевищує середнього геометричного від початкових значень автокореляційних функцій окремих процесів:
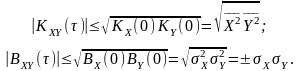
Функція взаємної кореляції двох нецентрованих незалежних процесів (не обов’язково стаціонарно-зв’язаних) дорівнює добуткові їхніх математичних очікувань, а центрованих – нулю:
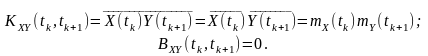
Наведена властивість є наслідком властивості середньостатистичного значення за відповідних вимог до процесів співмножників.
;
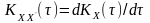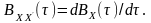
Дійсно, якщо враховувати, що за означенням похідної
,
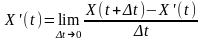а результатом диференціювання стаціонарного процесу є процес також стаціонарний, то функція взаємної кореляції
.
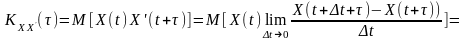
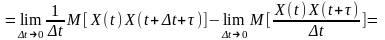
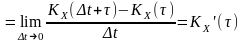Як
відомо, початкове значення
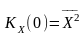функції автокореляції
є її максимальним значенням. Ураховуючи,
що
– є функцією парною, початкове значення
функції взаємної кореляції, а отже, і
похідної від функції автокореляції
.
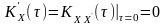Це означає, що миттєві значення
стаціонарно-зв’язаних
процесів
і
у
співпадаючих перерізах є некорельованими
величинами, але статистично залежними.
Однак, у разі стаціонарного процесу
з нормальним законом розподілу
ймовірностій такий процес і його похідна
є не тільки некорельованими, а і
статистично незалежними.
ПІДСУМКИ |
|
1. Стаціонарно-зв’язаними можуть бути тільки процеси, кожен з яких задовольняє умови стаціонарності. 2. Миттєві значення стаціонарно-зв’язаних процесів і у співпадаючих перерізах є некорельованими величинами, але статистично залежними. Однак, стаціонарний процес з нормальним законом розподілу ймовірностей і здиференційований процес є не тільки некорельованими, а і статистично незалежними.
|
3. Якщо два процеси є стаціонарними, але не стаціонарно-зв’язаними, то функція взаємної кореляції буде залежати як від початку відліку часу , так і часового інтервалу . 4. Для стаціонарно-зв’язаних процесів миттєве значення їхньої взаємної кореляційної функції не перевищує середнього геометричного від початкових значень їхніх автокореляційних функцій. 5. Функція взаємної кореляції двох нецентрованих незалежних процесів (не обов’язково стаціонарно-зв’язаних) дорівнює добуткові їхніх математичних очікувань, а центрованих – нулю. 6. Форумли для визначення взаємних функцій кореляції стаціонарно-зв’язаних процесу і процесу, що є результатом його диференціювання: ;
|