Процесу (а) та похідної від нього (б).

Приклад. Визначити кореляційну функцію процесу на вході лінійної системи у вигляді класичного послідовного RC-кола першого порядку (рис. 9.4), якщо реакція такої системи є процесом стаціонарним із кореляційною функцією .

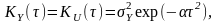
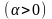Раніше показано, що процес X(t)=Y(t)+Z(t), де 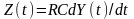- диференціальне перетворення стаціонарного випадкового процесу (СВП) Y(t), а отже, є процесом також стаціонарним. Оскільки функціональний зв’язок між процесами Z(t) та Y(t) відрізняється від прямо пропорційного, то це процеси некорельовані. Тоді, АКФ 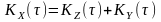вхідного процесу, як кореляційна функція суми некорельованих стаціонарних випадкових процесів.

Відомо, що диференціальне перетворення СВП Y(t) дає процес 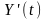із кореляційною функцією 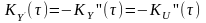. Процес 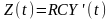, де RC – невипадкова величина, характеризується АКФ 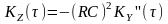. Отже, для вхідного процесу

.

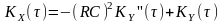Двократне диференціювання 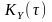дає

.

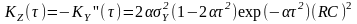Остаточно

.

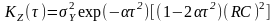Інтегрування процесів. Тепер зупинимось на інтегральному перетворенні випадкового процесу , що дає випадковий процес

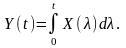
Такий зв’язок має місце в ідеальних інтегруючих системах між реакцією та дією.

Будемо вважати, що – нестаціонарний процес із кореляційною функцією (або для центрованих процесів) чи 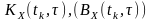. Згідно з наведеними раніше висновками відносно дії операторів лінійних систем на моментні функції їхніх реакцій середнє значення інтегралу від випадкової функції дорівнює інтегралу її середнього значення:

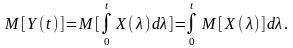(9.6)

Враховуючи це, маємо функцію кореляції процесу, який є результатом інтегрального перетворення:

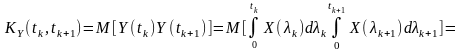
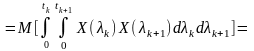(9.7)

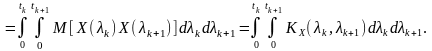
Отже, як і у випадку диференціювання процесів, кореляційна функція процесу , що визначається інтегралом заданого , є результатом послідовної дії оператора системи (в данному випадку інтегрування) на кореляційну функцію вхідного процесу:

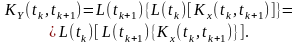(9.8)

Якщо процес є стаціонарним, тоді, як відомо,

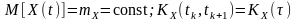, де .

Враховуючи (8.21) та (8.22), дістанемо математичне очікування

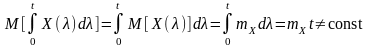(9.9)

та кореляційну функцію

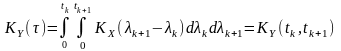(9.10)

випадкового процесу, який є результатом інтегрування стаціонарного.

• Математичне очікування випадкового процесу, що є результатом інтегрування стаціонарного, є функцією часу, а його кореляційна функція залежить як від початку відліку часу, так і відстані між перерізами.

Останні співвідношення та висновки засвідчують, що інтегральне перетворення стаціонарних процесів дає процес нестаціонарний.

Випадковий процес Вінера.

Випадковий стаціонарний процес який характеризується дельтоподібною функцією кореляції 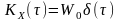та нульовим математичним очікуванням 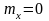, де 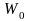- постійний множник. називають білим шумом, а його інтегральне перетворення - випадковим процесом Вінера.

Функція кореляції, математичне очікування та дисперсія випадкового процесу Вінера.

Математичне очікування 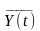процесу Y(t) визначимо за формулою

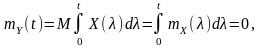
оскільки .

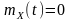Відповідно функція кореляції

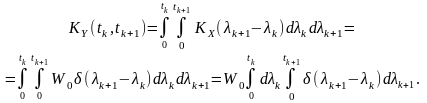
Значення змінних інтегрування 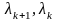є такими, що визначають область інтегрування прямокутної форми ОМРН зі сторонами 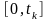та 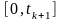(рис. 8.9). Відповідно до властивостей 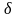- функції та функції 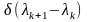внутрішній інтеграл дорівнює нулю для всіх пар значень 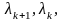крім таких, що задовольняють умову 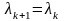, тобто одночасно належать прямій ОА, яка проходить через початок координат із кутом нахилу до осі абсцис 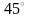, та прямій ВС .

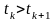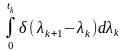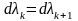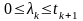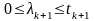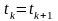Тоді, якщо (рис 9.5а), для вказаних пар значень інтеграл дорівнює одиниці; ; ; , а . У зв’язку з чим функція кореляції .

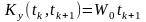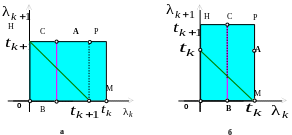
Рисунок 9.5 - До визначення функції кореляції вінеровського