
- •1.Закони розподілу випадкових процесів процесів
- •2. Одновимірні інтегральний та диференціальний закони розподілу
- •Неперервного (а), дискретного (б) та змішаного (в) процесів.
- •Закони розподілу ймовірностей дискретного процесу.
- •Щільності (б) ймовірностей дискретного процесу.
- •1 Загальна характеристика моментних функцій
- •2.Порядок та розмірність момент них функцій
- •3.Початкові моментні функції. Структура формул
- •4 Одновимірні моментні функції першого порядку
- •1.Одновимірні моментні функції другого порядку
- •Очікуваннями і різними дисперсіями.
- •Процесів із однаковими математичними очікуваннями
- •Початковою фазою: а – реалізації випадкового процесу;
- •1.Обчислення одновимірних моментних функцій за характеристичними.
- •2. Поновлення одновимірних характеристичних функцій за моментними.
- •6.1 Види статистичної залежності
- •Кореляцією (б) та некорельовані величини (в).
- •6.2 Двовимірні моментні функції другого порядку
- •7.1 Вкф двох випадкових процесів
- •Його кореляційна функція (б).
- •7.2 Нормовані кореляційні функції.
- •7.3 Особливості кореляційних характеристик
- •1 Визначення стаціонарності у вузькому та широкому значеннях
- •8.2 Математичне очікування,середній квадрат,дисперсія свп
- •8.3 Властивості акф нецентрованого та центрованого свп
- •Процесу (а) та похідної від нього (б).
- •Випадкового процесу.
- •3.Практичне застосування вкф для вирішення проблем виділення слабкого сигналу з суміші.
- •1. Визначення ергодичних випадкових процесів
- •2. Достатні умови ергодичності свп. Умова Слуцького
- •Спектральні характеристики випадкових процесів
- •1. Постановка задачі спектрального аналізу вп
- •2. Енергетичний спектр нестаціонарного вп та його зв'язок з кореляційною функцією.
- •3.Спектральна щільність потужності свп та її фізичний зміст. Спектр флуктуацій (центрованого) свп. Середній квадрат (дисперсія) та спектр свп.
- •4. Властивості спектральної щільності потужності свп. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп
- •5. Спектр монохроматичного свп. Односторонній та двохсторонній, фізичний та математичний спектри свп
- •1. Теорема Вінера-Хінчина. Обмеження, що накладаються на акф свп. Додатньо-визначені акф.
- •1.Постановка задачі кореляційного аналізу лінійних систем при дії свп
- •3.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
- •4.Статистичні характеристики реакції лінійної системи на дію "білого шуму".
- •5.Автокореляційна функція реакції. Згортка акф дії та імпульсної характеристики.
- •6. Кореляція процесів на вході та виході лінійної системи. Оцінка статистичного зв'язку "білого шуму" та реакції на нього лінійної системи.
- •З урахуванням властивості дзеркальної симетрії
- •Дійсно,
- •1.Аналіз у частотній області.
- •4. Спектральний аналіз інтегруючої системи при дії "білого шуму".
- •5. Енергетичний спектр реакції ідеального диференціатора.
- •На нього ідеального диференціатора (б).
8.3 Властивості акф нецентрованого та центрованого свп
Водночас, незмінність у часі тільки цих двох характеристик не є підставою вважати процес стаціонарним у вузькому значенні.
Розглянемо
тепер друге рівняння системи (8.1). Воно
справджується за будь-якого зсуву
,
у тому числі і для
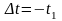 ,
що відповідає перенесенню початку
відліку часу в точку нуль (початок
координат).
,
що відповідає перенесенню початку
відліку часу в точку нуль (початок
координат).
У результаті
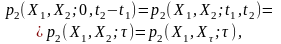
де

Стаціонарність
випадкового процесу означає інваріантність
двовимірної функції щільності ймовірностей
до окремо взятих моментів часу
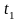 та
та
 і її залежність тільки від відстані між
ними.
і її залежність тільки від відстані між
ними.
Оскільки, двовимірна функція щільності ймовірностей визначає кореляційні характеристики (двовимірні моментні функції другого порядку), то для нецентрованого стаціонарного процесу його автокореляційна функція

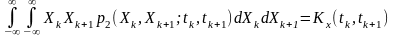 .
.
Вважатимемо,
що
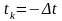 ,
тоді
,
тоді
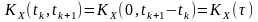 ;
;
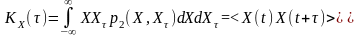 .
.
Отже,
функція
автокореляції стаціонарного випадкового
процесу є функцією не моментів визначення
перерізів
 ,
а тільки відстані між ними.
,
а тільки відстані між ними.
Звідси випливає, що
функція кореляції стаціонарного випадкового процесу є характеристикою статистичного зв’язку між його миттєвими значеннями в перерізах, що розміщені на відстані , незалежно від того на якій ділянці процесу вибрані ці перерізи.
Такі ж висновки та співвідношення можна отримати для функцій автокореляції та коефіцієнта автокореляції центрованого стаціонарного випадкового процесу:
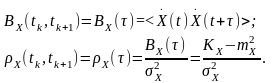
Випадкові процеси, які характеризуються не тільки постійними математичним очікуванням, середнім квадратом та дисперсією, а також кореляційними функціями одного аргументу , як відстані між перерізами, називають стаціонарними у широкому значенні.
У означенні стаціонарного в широму розумінні випадкового процесу важливим є припущення скінченності дисперсії та математичного очікування.
Приклад.
Випадковий
процес X(t)
утворено реалізаціями
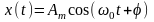 ,
де Am
та 0
є величинами сталими, а початкова фаза
– випадкова величина з рівномірним
законом розподілу
в інтервалі
.
Визначити кореляційну функцію процесу.
,
де Am
та 0
є величинами сталими, а початкова фаза
– випадкова величина з рівномірним
законом розподілу
в інтервалі
.
Визначити кореляційну функцію процесу.
Раніше
було показано, що рівномірному закону
розподілу
відповідає синусоподібний закон
розподілу для заданого процесу
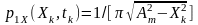 ,
математичне очікування якого дорівнює
нулю:
,
математичне очікування якого дорівнює
нулю:
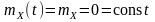 ,
а дисперсія
,
а дисперсія
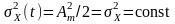 .
Ці результати безпосередньо випливають
із незалежності
від змінної часу
.
.
Ці результати безпосередньо випливають
із незалежності
від змінної часу
.
Тоді кореляційна функція заданого процесу
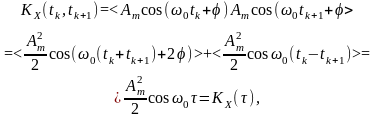
де враховано, що математичне очікування суми процесів дорівнює сумі математичних очікувань складових, а математичне очікування числа є саме число.
Таким чином, заданий випадковий процес задовольняє всі умови, потрібні для того, щоб забезпечити стаціонарність у широкому значенні.
Приклад. Випадковий процес утворено реалізаціями гармонічної форми з амплітудою Am, що є випадковою величиною з довільним законом розподілу, а частота та початкова фаза - дійсні числа.
Математичне
очікування такого процесу
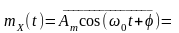
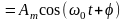 не залежить від часу тільки тоді, коли
середнє значення
не залежить від часу тільки тоді, коли
середнє значення
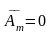 .
Отже, в загальному випадку процес, що
розглядається, буде нестаціонарним.
.
Отже, в загальному випадку процес, що
розглядається, буде нестаціонарним.
За
нульового зсуву між перерізами (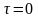 )
автокореляційна функція нецентрованого
стаціонарного випадкового процесу
дорівнює його середньому квадрату,
центрованого – дисперсії, а коефіцієнт
автокореляції – одиниці:
)
автокореляційна функція нецентрованого
стаціонарного випадкового процесу
дорівнює його середньому квадрату,
центрованого – дисперсії, а коефіцієнт
автокореляції – одиниці:
 .
(8.4)
.
(8.4)
Це випливає із означення вказаних функцій:
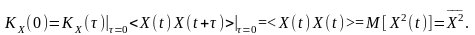
Функції кореляції стаціонарних процесів є парними відносно зсуву (властивість парної симетрії):
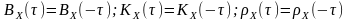 .
(8.5)
.
(8.5)
Раніше була доведена властивість симетрії в загальному випадку. Наприклад, для нецентрованого випадкового процесу
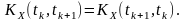
Для стаціонарного процесу
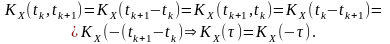
Властивість парної симетрії або парності дає змогу обчислювати функції кореляції тільки для додатних значень її аргументу , а результат для від’ємних визначати на її основі.
Найбільшого значення функція кореляції набуває, зазвичай, за нульового значення її аргументу. Для періодичних процесів можна вказати і інші значення аргументу, за яких функції кореляції набувають такого самого значення, що і при . Тому вважається:
значення функції кореляції для будь-яких значень її аргументу за абсолютним значенням не перевищують тих, що визначаються нульовим значенням аргументу:
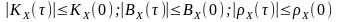 .
(8.6)
.
(8.6)
Відомо, що середнє значення випадкового процесу, що не набуває від’ємних значень, є невід’ємним.
Дійсно,
для процесу
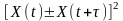 ,
коли
є стаціонарним процесом, його математичне
очікування
,
коли
є стаціонарним процесом, його математичне
очікування

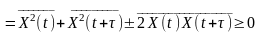 .
.
Тоді
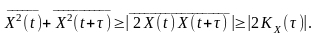
Для
стаціонарних процесів
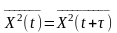 ,
тому
,
тому
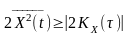
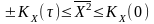 .
.
Зв’язок
між кореляційною функцією
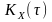 нецентрованого та
нецентрованого та
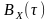 центрованого стаціонарного випадкового
процесу відображається такою формулою:
центрованого стаціонарного випадкового
процесу відображається такою формулою:
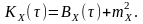 (8.7)
(8.7)
Функція кореляції випадкового нецентрованого стаціонарного процесу з ненульовим математичним очікуванням містить в собі постійну складову (рис. 8.2, б).
У
разі, якщо
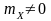 справедливість наведеного твердження
випливає з формули (8.7).
справедливість наведеного твердження
випливає з формули (8.7).
Розглянемо
випадковий процес
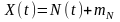 .
Припустімо, що
.
Припустімо, що
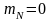 .
Тоді автокореляційна функція
.
Тоді автокореляційна функція
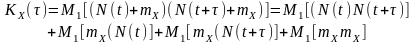
 ,
,
де
враховано, що для стаціонарного процесу
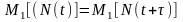 .
.
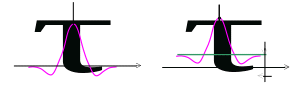
Рисунок 8.2 - До зв’язку між кореляційними функціями центрованого та нецентрованого випадкових стаціонарних процесів.
Зважаючи на те, що , остаточно отримаємо:

Кореляційна
функція
 алгебраічної суми некорельованих чи
незалежних центрованих процесів
і
дорівнює алгебраїчній сумі кореляційних
функцій його складових:
алгебраічної суми некорельованих чи
незалежних центрованих процесів
і
дорівнює алгебраїчній сумі кореляційних
функцій його складових:
 (8.8)
(8.8)
Раніше
було встановлено, що якщо центровані
процеси
і
незалежні, отже і некорельовані, то їхня
взаємна кореляційна функція
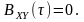
Тоді
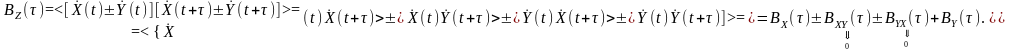
Слід зазначити, що цей висновок є справедливим для будь-яких процесів, необов’язково стаціонарних:
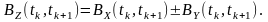
Кореляційна
функція
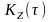 алгебраічної суми некорельованих чи
незалежних нецентрованих процесів
і
дорівнює алгебраїчній сумі кореляційних
функцій складових та подвоєного добутку
їхніх математичних очікувань:
алгебраічної суми некорельованих чи
незалежних нецентрованих процесів
і
дорівнює алгебраїчній сумі кореляційних
функцій складових та подвоєного добутку
їхніх математичних очікувань:
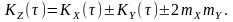 (9.9)
(9.9)
Ця властивість доводиться аналогічно попередній із урахуванням того, що взаємна кореляційна функція незалежних, а значить, некорельваних центрованих процесів (необов’язково стаціонарних)
Кореляційна
функція
процесу
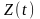 ,
що є добутком двох незалежних випадкових
процесів
і
,
дорівнює добуткові кореляційних функцій
співмножників:
,
що є добутком двох незалежних випадкових
процесів
і
,
дорівнює добуткові кореляційних функцій
співмножників:
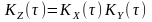 .
(8.10)
.
(8.10)
За означенням автокореляційної функції та з урахуванням того, що математичне очікування добутку незалежних процесів визначається добутком їхніх математичних очікувань, маємо:
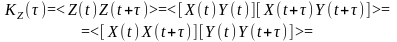
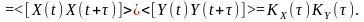
Аналогічний висновок справджується також для центрованих процесів і сигналів:
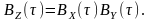
Слід звернути увагу на те, що властивість «добутку» є справедливою і для нестаціонарних процесів.
Кореляційна функція періодичного процесу є періодичною того самого періоду.
►Приклад.
Випадковий
процес
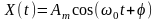 із рівномірним законом розподілу
початкової фази, як було встановлено
раніше, характеризується кореляційною
функцією
із рівномірним законом розподілу
початкової фази, як було встановлено
раніше, характеризується кореляційною
функцією
 ,
(8.11)
,
(8.11)
що
є періодичною з періодом процесу
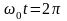
Лекція 9. Диференціальне та інтегральне перетворення СВП.
Кореляційна функція процесу, що є диференціальним перетворенням від заданого СВП. Процеси диференційовані та недиференційовані. Дисперсія недиференційованого СВП. Інтегральне перетворення СВП. МО, середній квадрат, дисперсія та АКФ інтеграла від СВП. Процес Вінера як інтегральне перетворення СВП типу "білий шум".
Література [ 7, с. 104-109; 9, с. 201-209; 1, 2].
Дуже важливим видом перетворень процесів, у тому числі і випадкових, є їхнє диференціювання та інтегрування. Очевидно, що під час теоретичного дослідження таких перетворень слід мати в розпорядженні залежності, які б відображали зв’язок між статистичними характеристиками об’єктів таких операцій.
Диференціювання
процесів. Розглянемо
деякий випадковий процес
.
Припустимо, що існує його похідна
 .
Як лінійна операція диференціювання
випадкової функції, дає функцію випадкову.
В теорії випадкових процесів вважається,
що
.
Як лінійна операція диференціювання
випадкової функції, дає функцію випадкову.
В теорії випадкових процесів вважається,
що
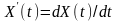 є похідною випадкового процесу
,
якщо справджується така умова:
є похідною випадкового процесу
,
якщо справджується така умова:
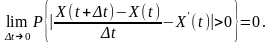 (9.1)
(9.1)
З формули (9.1) випливає, що статистичні властивості процесу, який є результатом диференціювання, визначаються різницею миттєвих значень початкового процесу , рознесених у часі на відстань .
Обчислимо
математичне очікування випадкового
процесу
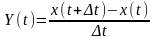 .
Будемо вважати, що за
певного часового
зсуву
процес
.
Будемо вважати, що за
певного часового
зсуву
процес
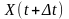 є
копією процесу
.
У цьому разі випадкові процеси називаються
стаціонарними.
Тоді, з урахуванням властивостей
математичного очікування, маємо:
є
копією процесу
.
У цьому разі випадкові процеси називаються
стаціонарними.
Тоді, з урахуванням властивостей
математичного очікування, маємо:
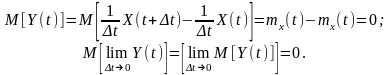
Диференціювання випадкового стаціонарного процесу дає процес із нульовим математичним очікуванням.
Якщо процес не є стаціонарним, то
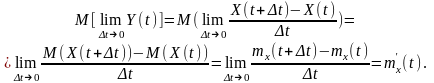
Математичне очікування процесу, що є похідною від заданого нестаціонарного процесу, визначається похідною від математичного очікування останнього.
Отже, якщо два випадкові процеси пов’язані операцією диференціювання, то у загальному випадку відповідні їм математичні очікування також пов’язані такою самою операцією.
середні
значення (математичні очікування)
процесів на вході та виході лінійної
системи, властивості якої описуються
лінійним операторм
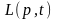 ,
пов’язані
тим самим оператором.
,
пов’язані
тим самим оператором.
Зрозуміло, що необхідною умовою стаціонарності випадкового процесу є незмінність в часі його математичного очікування. Саме за таких умов операція диференціювання дає нульове значення.
Приклад.
Визначити
математичне очікування процесу на
виході ідеального диференціатора, якщо
на його вході діє випадковий процес із
середнім значенням
 .
.
Оскільки вихідний та вхідний процеси зв’язані оператором диференціювання, математичне очікування реакції ідеального диференціатора
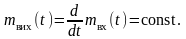
П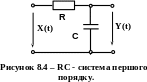 риклад.
Визначити
середнє значення процесу X(t)
на вході лінійної системи у вигляді
класичного послідовного RC-кола
першого порядку (приклад інтегруючої
системи; рис. 8.4), якщо її реакція
риклад.
Визначити
середнє значення процесу X(t)
на вході лінійної системи у вигляді
класичного послідовного RC-кола
першого порядку (приклад інтегруючої
системи; рис. 8.4), якщо її реакція
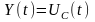 є процесом стаціонарним із математичним
очікуванням
є процесом стаціонарним із математичним
очікуванням
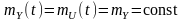 .
.
Як відомо зв’язок між реакцією Y(t) та дією в такій системі описується диференціальним рівнянням
 .
.
Процес
X(t)
є сумою двох процесів: X(t)=Y(t)+Z(t),
де
 з точністю до постійного множника є
диференціальним перетворенням процесу
.
Тоді з урахуванням властивостей
математичного очікування та зроблених
попередньо висновків
з точністю до постійного множника є
диференціальним перетворенням процесу
.
Тоді з урахуванням властивостей
математичного очікування та зроблених
попередньо висновків
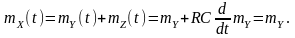
Я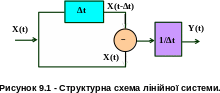 к
відомо, для кількісного оцінювання
статистичного зв’язку між миттєвими
значеннями процесу слід знати його
автокореляційну функцію. Розглянемо
функцію кореляції процесу
к
відомо, для кількісного оцінювання
статистичного зв’язку між миттєвими
значеннями процесу слід знати його
автокореляційну функцію. Розглянемо
функцію кореляції процесу
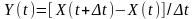 .
Такий
процес
можна розглядати як результат лінійних
перетворень над процесом
на зразок затримка в часі на величину
,
віднімання (алгебраїчне додавання) та
множення (підсилення, повторення або
послаблення). Структурна схема лінійної
системи, що реалізує ці функції, показана
на рис. 9.1
.
Такий
процес
можна розглядати як результат лінійних
перетворень над процесом
на зразок затримка в часі на величину
,
віднімання (алгебраїчне додавання) та
множення (підсилення, повторення або
послаблення). Структурна схема лінійної
системи, що реалізує ці функції, показана
на рис. 9.1
За означенням
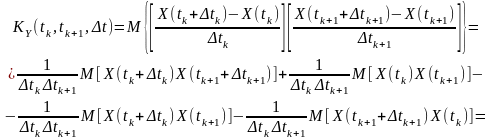 (9.2)
(9.2)
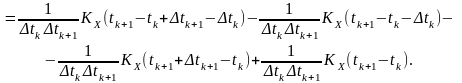
Кореляційну
функцію
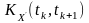 здиференційованого
процесу
,
отримаємо граничним переходом у
останньому співвідношенні, спрямувавши
до нуля
здиференційованого
процесу
,
отримаємо граничним переходом у
останньому співвідношенні, спрямувавши
до нуля
 та
та
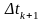 :
:
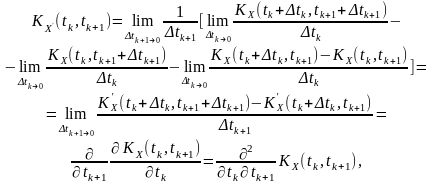 (9.3)
(9.3)
де
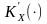 позначено похідну від
за
аргументом
.
позначено похідну від
за
аргументом
.
►Приклад.
Випадковий
процес X(t)
характеризується
кореляційною функцією
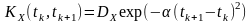 .
Знайти середній квадрат процесу Y(t)
на
виході ідеального диференціатора.
.
Знайти середній квадрат процесу Y(t)
на
виході ідеального диференціатора.
Згідно з (9.3) кореляційна функція вихідного процесу
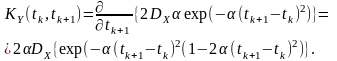
За
властивостями кореляційної функції
середній квадрат визначається її
значенням у співпадаючих перерізах:
 .
Тоді отримаємо
.
Тоді отримаємо
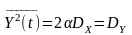 .
Результатом є стала дисперсія, а отже,
математичне очікування вихідного
процесу дорівнює нулю.
.
Результатом є стала дисперсія, а отже,
математичне очікування вихідного
процесу дорівнює нулю.
Для стаціонарного процесу функції кореляції не залежать від початку відліку часу, моментів визначення перерізів, а визначаються відстанню між перерізами. Це дає змогу переписати співвідношення (9.2) у такому вигляді:
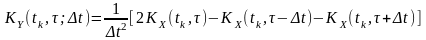 .
.
Спрямовуючи
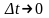 ,
обчислимо кореляційну функцію похідної
,
обчислимо кореляційну функцію похідної
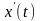 ,
як границю останього співвідношення:
,
як границю останього співвідношення:
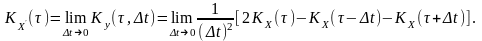
За умови, що , чисельник та знаменик прямують до нуля. Розкривши невизначеність за правилом Лопіталя відносно , дістанемо:
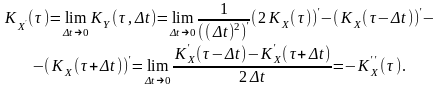
Враховано,
що похідна від складної функції з
від’ємним
аргументом (-
)
дає
знак
мінус перед
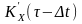 ,
а також те, що функція
не залежить від
.
Тому під
час застосування
правила Лопіталя відносно
маємо:
,
а також те, що функція
не залежить від
.
Тому під
час застосування
правила Лопіталя відносно
маємо:
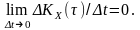
Кореляційна функція
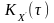 процесу
,
що є похідною від стаціонарного процесу
,
дорівнює взятій із знаком мінус похідній
другого порядку від кореляційної
функції
початкового процесу:
процесу
,
що є похідною від стаціонарного процесу
,
дорівнює взятій із знаком мінус похідній
другого порядку від кореляційної
функції
початкового процесу:
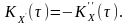 (9.4)
(9.4)
Такий самий висновок є справедливим і для кореляційних функцій здиференційованих центрованих процесів:
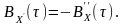 (9.5)
(9.5)
Виходячи з означення кореляційної функції, очевидні і такі співвідношення:
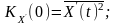
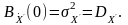
Отже, умовою диференціювання стаціонарного випадкового процесу є існування другої похідної від його автокореляційної функції.
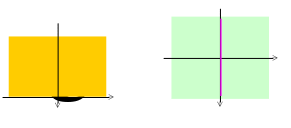
Рисунок 9.2- Кореляційна функція експоненціального виду (а)
та її похідна (б).
Але не будь-яка кореляційна функція задовольняє умову існування похідної другого порядку від неї. Наприклад, кореляційна функція, що зображена на рис. 9.2, а, перща похідна від якої має розрив першого роду для нульвого значення аргументу (рис. 9.2, б) на відміну від функції кореляції, зображеної на рис. 9.3, а. Можна сподіватися, що якщо в околі точки =0 для функції кореляції характерні незначні зміни, то похідна другого порядку від неї в цій точці існує (рис.
9.3, б).
Відомо, що уповільнення кореляційної функції відображає достатньо високий рівень статистичного зв’язку між миттєвими значеннями процесу в близьких перерізах. Для процесу, який подається кореляційною функцією, зображеною на рис. 9.2, а, такий зв’язок є слабким.
Якщо
випадковий процес
диференціюється
разів, то необхідною умовою цього повинно
бути існування всіх
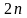 похідних від його кореляційної функції.
Отже, кореляційні функції трикутної та
експоненціальної форми мають розрив
похідної для нульового значення її
аргумента. У цьому разі друга похідна
приймає нескінченне значення.
похідних від його кореляційної функції.
Отже, кореляційні функції трикутної та
експоненціальної форми мають розрив
похідної для нульового значення її
аргумента. У цьому разі друга похідна
приймає нескінченне значення.

Рисунок 9.3 - Кореляційна функція нормального виду (а) та
її похідна (б).
Випадкові процеси, автокореляційні функції яких не задовольняють умову існування другої похідної від них за нульового значення аргументу, називаються недиференційованими.
Дисперсія (середньоквадратичне значення) процесу, який є результатом диференціювання недиференційованого випадкового процесу, дорівнює нескінченності. Виходячи з ототожнення середного квадрата (дисперсії) процесу з його потужністю, можна зробити висновок, що існування в природі випадкових процесів із автокореляційними функціями вказаного типу неможливе, як немає фізичного змісту процес із нескінченною потужністю. Однак, незважаючи на це, автокореляційні функції на зразок трикутника та симетричної експоненти є корисними моделями для диференційованих процесів.
Приклад.
Визначити
функцію кореляції та дисперсію похідної
центрованого процесу
,
автокореляційна функція якого
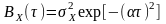
Здиференціювавши послідовно два рази , дістанемо:

Остаточно

Дисперсія здиференційованого процесу
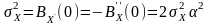 .
.
Графіки
функцій
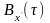 та
та
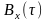 зображено на рис.9.4.
зображено на рис.9.4.

Рисунок 9.4 - Кореляційні характеристики центрованого
