1 Визначення стаціонарності у вузькому та широкому значеннях
Стаціонарні випадкові процеси є зручною математичною моделлю та достатньо точною апроксимацією реальних фізичних явищ.
Будь-який
випадковий процес
характеризується або ймовірнісними,
або часовими характеристиками, які
визначені на основі ймовірнісних. Такі
характеристики базуються на поданні
випадкового процесу
системою із однієї, двох, трьох чи, в
загальному випадку,
випадкових величин
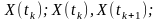відповідно для вибраних перерізів у
точках
.
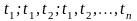Випадковий
процес називається стаціонарним
у вузькому
значенні,
якщо
закони розподілу ймовірностей будь-якого
порядку, що описують його властивості,
не залежать від вибору початку відліку
часу, тобто не змінюються, якщо всі
моменти
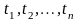зсунути на довільний інтервал часу
.
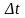У випадках, коли хоча б один із законів розподілу (будь-якого порядку) змінюється при зсуві початку відліку часу, то випадковий процес вважається нестаціонарним.
Приклад.
Припустімо,
що в перерізі
випадковий процес X(t)
характеризується одновимірною функцією
щільності ймовірностей
.
При переході до перерізу в точці
+
маємо
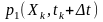Якщо
останній закон буде відрізнятись від
,
то можна однозначно стверджувати, що
процес X(t)
є
нестаціонарним.
умовою стаціонарності процесу у вузькому значенні є незалежність його ймовірнісних характеристик всіх порядків від 1 до n без виключення від вибору моменту відліку часу:
;
;
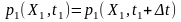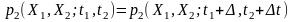(8.1)
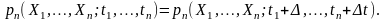
Системі рівнянь (8.1) можна поставити у відповідність еквівалентне співвідношення
,
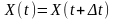(8.2)
із якого випливає, що
стаціонарна у вузькому значенні випадкова функція переходить сама в себе під час довільного зсуву в часі на всіх її реалізацій.
Останнє може означати і таке:
стаціонарний випадковий процес розвивається в часі нескінченно довго; він немає ні початку, ні кінця.
Із урахуванням (8.2) для стаціонарного у вузькому значенні процесу, наприклад,
,
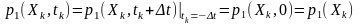(8.3)
Тоді
справедливою є форма запису одновимірного
диференціального закону
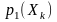без часового аргументу, що відповідає
фіксованому моменту часу.
8.2 Математичне очікування,середній квадрат,дисперсія свп
Математичне
очікування випадкового
процесу
в перерізі
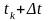для довільного зсуву
з урахуванням (8.3) є таким:
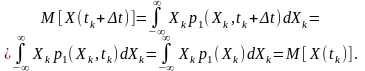
Отже,
середнє значення стаціонарного у вузькому значенні випадкового процесу у всіх перерізах є однаковим.
Тоді
можна записати:
.
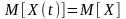Очевидно, що середній квадрат та дисперсія стаціонарного у вузькому значенні випадкового процесу, які визначаються через , також є характеристиками не окремих його перерізів, а процесу в цілому, тобто є величинами постійними та незалежними від часової змінної:
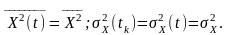
Зауважимо також і таке, що дисперсії та математичні очікування стаціонарних у вузькому значенні випадкових процесів можуть бути нескінченними.
Незмінність
в часі математичного очікування
стаціонарного процесу означає, що при
графічному зображенні всі його реалізації
будуть проходити над віссю абсцис (при
;
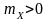рис. 8.1, а),
під нею (при
;
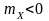рис. 8.1, б).
Якщо середнє значення дорівнює нулю,
то відхилення реалізацій в середньому
в додатню чи від’ємну
сторону (вверх чи вниз) будуть однаковими
(рис. 9.1, в).
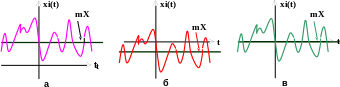
Рисунок 8.1.- Приклад реалізації стаціонарного випадкового процесу:
а – математичне очікування додатне; б – математичне очікування від’ємне; в – математичне очікування дорівнює нулю.
Підсумовуючи, стверджуємо, що,
якщо середнє значення чи дисперсія не постійні величини, то це є достатнім, щоби вважати процес нестаціонарним.