7.3 Особливості кореляційних характеристик
Фізичний зміст кореляційних характеристик. Очевидно, що розмірність автокореляційної функції нецентрованого процесу визначається розмірністю квадрата його миттєвого значення, а взаємної кореляційної функції – розмірністю добутку миттєвих значень процесів. Можна стверджувати також, що для конкретних значень та значення кореляційної функції пропорційні потужності взаємодії миттєвих значень об’єкта (процесу або двох процесів) у перерізах та .
У
співпадаючих перерізах, коли
=
,
кореляційна функція
дорівнює середньому квадрату процесу
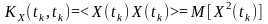і відображає потужність його миттєвого
значення в перерізі
.
Миттєві
значення кореляційних функцій центрованих
процесів визначають потужності взаємодії
відхилень випадкових процесів від
середніх значень. Водночас, для
співпадаючих перерізів, коли
=
,
функція взаємної кореляції
=
,
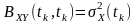тобто дисперсії, яка, як відомо,
характеризує середню потужність
випадкового центрованого процесу.
Об’єкти
з повною кореляцією. У
цьому разі між миттєвими значеннями
процесу
в перерізах
і
має місце лінійний зв’язок:
.
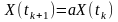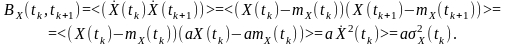
Таким
чином, при прямо пропорційній залежності
між миттєвими значеннями процесу в двох
різних моментах
часу функція кореляції центрованого
процесу
пропорційна
дисперсії одного з них. Якщо
,
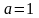то отримаємо попередній результат, що
відповідає співпаданню перерізів
та
.
Повна кореляція еквівалентна нульовому зсуву між перерізами. Чим більше зсув, тим менше кореляція.
З іншого боку, відомо, що математичне очікування добутку незалежних величин визначається добутком їхніх математичних очікувань. Припустимо, що та вибрані так, що незалежить від . Очевидно, це найбільш ймовірно для одного й того самого процесу, коли перерізи визначені в моменти часу, відстань між якими дуже велика.
Тоді
,
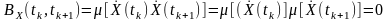оскільки
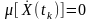і
.
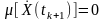Функція кореляції незалежних центрованих об’єктів дорівнює нулю.
Виходячи з отриманих раніше результатів, можна зробити такі висновки:
значення функції кореляції центрованих процесів змінюється в межах від 0 до
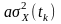або
;
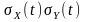незалежні випадкові величини або процеси є некорельованими з нульовими кореляційними функціями, а отже, енергетично не взаємодіють;
сильно корельовані величини (процеси) є “лінійно подібними”. У цьому разі форми вибіркових функцій (реалізацій) випадкового процесу або форми відповідних реалізацій двох процесів та - ідентичні;
характер зміни кореляційних функцій від аргументів , та відображає розвиток випадкового процесу в часі. Швидким змінам процесу відповідають швидкі зміни кореляційних функцій і навпаки.
Останнє випливає з того, що випадкові величини сильно корельовані, якщо та розміщені близько один від одного. Якщо за малих значень кореляція незначна, то таке можливе тільки за умови значної зміни характеру розвитку процесу в часі.
Взаємозв’язок між кореляційними функціями нецентрованого та центрованого випадкового процесів відображається такими формулами:
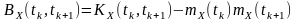
або
.
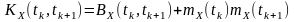Отже, якщо процеси є незалежними, то і вони є некорельовані. Останнє означає, що функція кореляції нецентрованого випадкового процесу
.
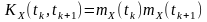Те саме справедливе для взаємних функцій кореляції.
Отже, двовимірні початкові та центральні моментні функції другого порядку (кореляційні функції нецентрованих та центрованих випадкових процесів) кількісно відображають величину статистичного зв’язку між вибірками в двох перерізах одного процесу чи одиночними вибірками в двох процесах. Значення цих функцій тісно зв’язані з дисперсіями та математичними очікуваннями.
ПІДСУМКИ |
|
1. Значення кореляційної функції пропорційні потужності взаємодії миттєвих значень процесу (двох процесів). 2. Швидким змінам процесів відповідають швидкі зміни кореляційних функцій і навпаки. 3. У разі сильно корельованих процесів форми вибіркових функцій (реалізацій) випадкового одного або двох процесів є ідентичними. |
4. Функція кореляції незалежних центрованих процесів дорівнює нулю, а процеси є некорельваними. 5. Повна кореляція еквіва-лентна нульовому зсуву між перерізами. Чим більше зсув, тим менше кореляція. 6. Функція кореляції нецентрованого випадкового процесу . |
Лекція 8. Стаціонарні випадкові процеси (СВП). Кореляційні властивості СВП.
Стаціонарність у вузькому та широкому значенні. МО, середній квадрат та дисперсія СВП. Властивості АКФ нецентрованих та центрованих СВП. Зв'язок між АКФ центрованих та нецентрованих СВП. Умови періодичності АКФ.
Література [ 7, с. 89-100; 10, с. 17-23; 9, с. 181-225; 3, 4 ].