7.2 Нормовані кореляційні функції.
Під час дослідження випадкових процесів та їхніх перетворень різноманітними системами часто користуються нормованими функціями кореляції центрованих процесів.
Для центрованого випадкового процесу нормована функція автокореляції
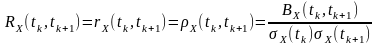
визначається як відношення функції кореляції центрованого випадкового процесу до добутку його середньоквадратичних відхилень у перерізах та .
Оскільки,
для
лінійно зв’язаних
величин
,
а для незалежних (некорельованих) -
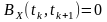, то можна стверджувати таке:
нормована функція автокореляції (коефіцієнт автокореляції), у двох крайніх випадках зв’язку між випадковими об’єктами за абсолютним значенням дорівнює нулю та одиниці.
Значення
нуль відповідає відсутності зв’язку
(статистичній незалежності) або наявності
функціонального зв’язку, що істотно
відрізняється від лінійного, а одиниця
- найбільш тісному (лінійному)
функціональному зв’язку. Природньо
вважати, що між цими двома крайніми
випадками, коли зв’язок існує, але не
є гранично жорстким, коефіцієнт кореляції
набуває значення між 0 та
.
Коефіцієнт
автокореляції
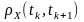можна вважати показником того, наскільки
змінюється потужність флуктуацій
випадкового процесу
при проходженні часу
,
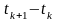починаючи з
,
або наскільки збереглась форма
в середньому за ансамблем. Значення
вказує на те, що форми вибіркових функцій
процесу
ідентичні, а при
- вибіркові функції некорельовані, тобто
не існує якого-небудь фрагменту вибіркової
функції
,
де
,
процесу
,
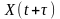який би був частиною вибіркової функції
процесу
.
Значення
засвідчує, що форма вибіркової функції
процесу
є дзеркальним відображенням стосовно
осі
вибіркової функції
процесу
.
Аналогічно
вводять поняття нормованої
функції кореляції двох центрованих
процесів
та
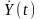або коефіцієнтів
взаємної кореляції:
- для процесів та
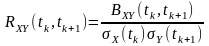
для процесів та
.
Висновки наведені для коефіціента автокореляції є справедливими і для коефіцієнтів взаємної кореляції.
Слід звернути увагу на те, що коефіціент кореляції в загальному випадку є функцією двох величин: моментів часу і , або та інтервалу . Очевидно, що із збільшенням статистичний зв’зок між миттєвими значеннями одного процесу або двох процесів та в неспівпадаючі моменти часу буде зменшуватись. Але для різних за динамікою процесів числові значення очевидно будуть різними. Ось чому випадкові процеси (їх розвиток у часі), як і детерміновані, характеризують ще одним параметром, що тісно пов’язаний з нормованими функціями кореляції, який називають інтервалом кореляції .
ПІДСУМКИ |
|
1.Конкретний вид кореляційної функції істотно залежить від порядку запису в її позначенні аргументів і індексів. 2. Із збільшенням відстані між перерізами статистичний зв’зок між миттєвими значеннями одного або двох процесів у неспівпадаючі моменти часу буде зменшуватись. |
3. Нормовані кореляційні функції набувають значень із діапазону [0, ±1]. |