7.1 Вкф двох випадкових процесів

Двовимірна початкова моментна функція другого порядку, визначена для двох випадкових процесів та , є середньостатистичним значенням добутку миттєвих значень процесу в перерізі чи та процесу відповідно в перерізі чи і називається взаємною кореляційною функцією (ВКФ) двох нецентрованих процесів або функцією взаємної кореляції.

На відміну від функції автокореляції, для якої =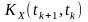 , взаємна кореляційна функція залежить як від порядку (послідовності) слідування аргументів, так і процесів (множників). Ось чому

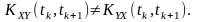
Структура формул, що застосовується під час обчислення кореляційних функцій двох процесів:

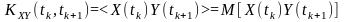(7.1)

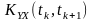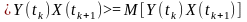= (7.2)

►Приклад. Визначити функцію кореляції процесу Х(t) кожна реалізація якого є послідовністю прямокутних відеоімпульсів тривалості 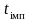(рис. 7.1, а), що набувають значення +A_m або -A_m з рівною ймовірностю:

Р(+A_m)=Р(-A_m)=0.5. (7.3)

Розглянемо дві випадкові величини Х(t₁) та Х(t₂)=Х(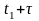 ), що відповідають моментам часу t₁, ._. Очевидно, що Х(t₁) та Х( ) є величинами дискретними, кожна з яких може набувати значення або +A_m або -A_m з безумовною ймовірностю відповідно до (7.3)Зважаючи на те, що імпульси різних знаків з’являються незалежно від того, який імпульс був перед цим, можна стверджувати, що у разі, якщо 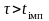, випадкові величини Х(t₁) та Х( ) є незалежними, а отже, некорельованими, і їхня функція автокореляції = .

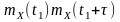Розглянемо випадок, коли 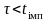. Тоді можлива ситуація, коли імпульс додатньої або від’ємної полярності “покриє” обидва перерізи t₁ та , а полярність (знак) величини Х( ) повністю визначається знаком Х(t₁). А це відповідає статистичній залежності між Х(t₁) та Х( ).

Для визначення функції кореляції потрібно знайти закон розподілу ймовірностей системи двох випадкових величин Х(t₁) та Х( ), а для розглядуваного прикладу ймовірності різних сполучень (комбінацій) можливих значень Х(t₁) та Х( ). У данному випадку таких сполучень чотири: (A_m, A_m); (A_m, -A_m); (-A_m, A_m); (-A_m, -A_m).

За означенням ймовірність Р(A_m, A_m)=Р(A_m)Р(A_m/A_m). Оскільки Р(A_m)=0,5, потрібно визначити умовну ймовірність того (події), що величина Х( ) набуде значення +A_m , якщо Х(t₁) набуває значення +A_m.

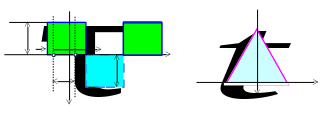
Рисунок 7.1 – Приклад дискретного випадкового процесу (а) та

Його кореляційна функція (б).

Така подія можлива у двох несумісних випадках:

А. Якщо додатний імпульс починається на відстані від точки t₁ меншій, ніж 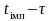(у цьому разі точка обов’язково перекривається ).

В. Якщо додатний імпульс розміщується від точки t₁ на відстані більшій, ніж , але наступний за ним імпульс буде також додатним.

Ймовірність події А відповідно до співвідношення мір, як одного з підходів до визначення ймовірності події, становить .

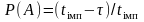Тоді ймовірність події В

=

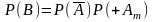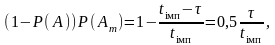
де 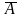– протилежна до А подія.

Остаточно, на основі теореми додавання :

.

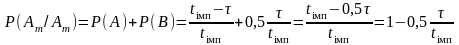Тоді шукана ймовірність:

.

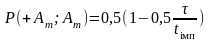Результати подібних міркувань до сумісного закону розподілу ймовірностей Х(t₁) та Х( )=Х(t₂) подані в таблиці 7.1.

Тоді згідно табл. 7.1 кореляційна функція

.

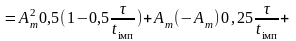
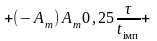
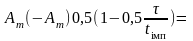
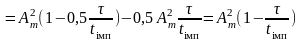Отже, за достатньо малих значень 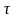ймовірність того, що Х(t₁) та Х( ) однакові (з урахуванням знаку) є дуже великою (близькою до 1). При збільшенні зв’язок між перерізами слабшає і при 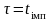дорівнює 0. Якщо поміняти місцями перерізи t₁ та t₂=t₁+ , то в наведених вище міркуваннях нічого не зміниться, проте у цьому разі 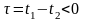стає від’ємним. Останнє вказує на симетрію функції кореляції відносно осі ординат. Графік кореляційної функції процесу, що розглядався, зображено на рис. 7.1, б.

Таблиця 7.1

X(t2)\X(t1)	+Am	-Am
+Am
-Am

◙

Двовимірні центральні моментні функції другого порядку є мірою статистичного зв’язку між миттєвими значеннями центрованих процесів і визначаються за такою формулою:

- для двох центрованих процесів

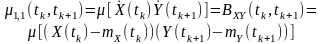(7.4)

або

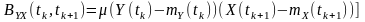. (7.5)

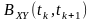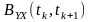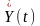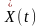Двовимірну центральну моментну функцію другого порядку або називають взаємною кореляційною функцією двох центрованих процесів відповідно і та і . Дуже часто функцію називають взаємною коваріаційною функцією двох нецентрованих процесів та .