Кореляцією (б) та некорельовані величини (в).

Наведемо графічну ілюстрацію сказаного на прикладі двох випадкових величин та . Домовимося, що кожній парі значень 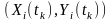відповідає на декартовій площині зображувальна точка. Тоді у разі, коли між величинами та є статистичний зв’язок, зображувальні точки розміщуються вздовж деякої прямої лінії, на яку повинні були б потрапляти у разі лінійного функціонального зв’язоку між величинами (рис. 6.2, а і б). Хаотичне розташування точок на площині характерне для незалежних, а отже, некорельованих величин (рис. 8.2, в). Зазначимо, що рис. 6.2, а описує величину із додатньою кореляцією, а рис. 8.2, б – від’ємною. Те саме можна було б сказати про випадкові величини і одного процесу або та двох процесів (сигналів) та .

ПІДСУМКИ
1. Одновимірні моментні функції першого порядку та другого порядків не повністю відображають динаміку випадкових процесів у часі. 2. Швидкість розвитку процесу в часі визначають ступенем імовірного зв’язку між миттєвими значеннями всіх його реалізацій у різних перерізах, розміщених на різній відстані один від одного та початку відліку.	. 3. Статистично незалежні величини (процеси) є некорельованими, водночас, некорельовані величини (процеси) не обов’язково є статистично незалежними.

6.2 Двовимірні моментні функції другого порядку

Моментна початкова двовимірна функція другого порядку 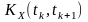випадкового процесу є середньостатистичним значенням добутку його миттєвих значень у перерізах, що відповідають моментам часу та :

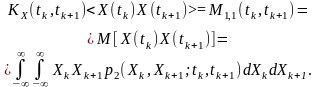(6.1)

Для дискретного випадкового процесу кореляційну функцію обчислюють за такою формулою:

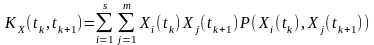(6.2)

При обчисленні сум використовують всі можливі сполучення (комбінації) значень та 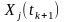. Величина 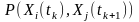відображає ймовірність того, що випадкова величина в перерізі набуде значення , а величина в перерізі значення і є законом розподілу двох випадкових величин та .

На підставі формули добутку ймовірностей випадкових величин та з урахуванням того, що сумісна ймовірність

,

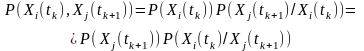формулу для моментної двовимірної функції другого порядку дискретних процесів можна записати у такому вигляді:

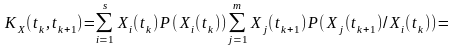
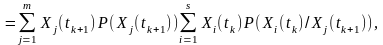(6.3)

де 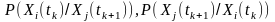- умовні закони розподілу ймовірностей величин та .

Для неперервних величин та

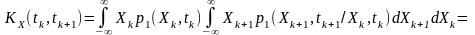
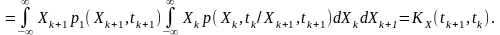
Отже, функція кореляції процесу наділена властивістю симетрії відносно моментів часу та , тобто є інваріантною відносно порядку слідування аргументів.

Двовимірна початкова моментна функція другого порядку , як міра статистичного зв’язку між миттєвими значеннями одного й того самого процесу , називається кореляційною функцією нецентрованого процесу, автокореляційною функцією (АКФ) або функцією автокореляції.

• Приклад. Визначити функцію кореляції випадкового процесу X(t) з нормальним законом розподілу між випадковими величинами та :

.

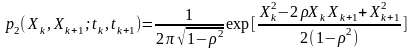За означенням кореляційна функція

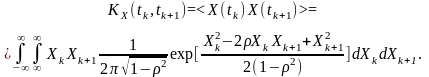
Подамо подвійний інтеграл у такому вигляді:

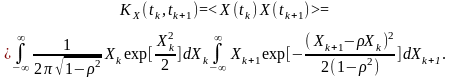
Внутрішній інтеграл

.

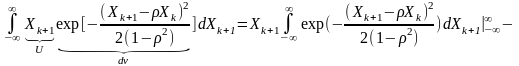
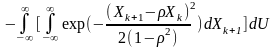Інтеграл

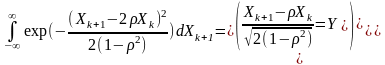
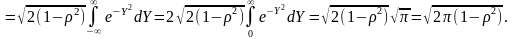
Ураховано, що останній визначений інтеграл є табличним і дорівнює .

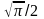Тоді

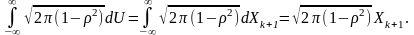
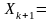
Якщо врахувати, що змінна Y для 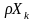дорівнює нулю, то .

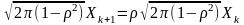Остаточно

=

.

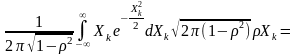
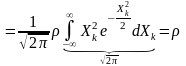Двовимірна центральна моментна функція другого порядку (АКФ)є мірою статистичного зв’язку між миттєвими значеннями центрованих процесів і визначаються за такою формулою:

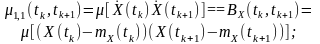(6.4)

Двовимірну центральну моментну функцію другого порядк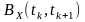у називають кореляційною функцією центрованого процесу . Дуже часто функцію називають коваріаційною функцією нецентрованого процесу .

Лекція 7. Кореляційні характеристики двох випадкоих процесів.

Взаємні кореляційні функції двох ВП. Особливості при різних видах зв'язку між миттєвими значеннями процесів. Фізичний зміст та властивості взаємної кореляційної функції. Неінваріантність до порядку слідування аргументів та процесів. Кореляційні характеристики алгебраїчної суми процесів з різним ступенем статистичного зв'язку між процесами.

Література [3, с. 122-154; 9, с. 191-222; 5, с. 161-202].

Завдання на СРС. Нормована кореляційна функція. Інтервал кореляції та способи його обчислення.