6.1 Види статистичної залежності

Середнє значення, середній квадрат, дисперсія та інші моментні функції першого та другого порядків як початкові, так і центральні, характеризують випадковий процес в одному перерізі, що відповідає точці , тобто в статиці, і є недостатніми для оцінок його динамічних властивостей. Ілюстрацією сказаного може служити співставлення двох процесів та , заданих вибірковими функціями на рис. 8.1. Наведені процеси характеризуються приблизно однаковими математичним очікуванням 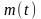та дисперсією 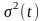. Однак, характер розвитку цих процесів у часі, їхня внутрішня структура істотно відрізняються. Для першого характерні повільні зміни в часі, для другого – швидкі. Отже, одновимірні моментні функції першого порядку не повністю відображають динаміку процесів у часі.

Швидкість розвитку процесу в часі визначають ступенем (рівнем) імовірного зв’язку між миттєвими значеннями всіх його реалізацій у різних перерізах, розміщених на різній відстані один від одного та початку координат. Про такий зв’язок йдеться також і стосовно двох або декількох процесів для відповідних перерізів у неспівдадаючі моменти часу. Кількісною мірою такого ймовірного зв’язку між миттєвими значеннями у двох перерізах, що відповідають довільним моментам часу , 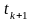, і є двовимірні моментні функції другого порядку з аргументами і або 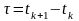і . Оскільки моментам часу і відповідають дві випадкові величини і 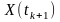для одного процесу (( і 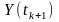- для двох процесів), то моментні функції другого порядку фактично відображають зміну в часі величини статистичної залежності між двома випадковими величинами.

Ймовірну залежність між випадковими величинами називають кореляцією між випадковими величинами. Ось чому моментні функції другого порядку ще називають функціями кореляції або кореляційними функціями.

Рисунок 6.1 - Процеси з різною динамікою.

Вважається, що ймовірна залежність займає проміжне місце між двома полярними формами залежності: одна – повна незалежність, тобто відсутність зв’язку; друга – найбільш жорстка функціональна.

Для ймовірних величин, подій чи процесів повна незалежність (статистична незалежність) означає, що закони розподілу ймовірностей одного об’єкта не залежать (не змінюються) від значень іншого. Для системи із випадкових величин останнє означає, що багатовимірна функція щільності ймовірностей подається добутком відповідних одновимірних щільностей:

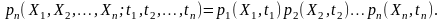
Функціональна залежність відображається деякою функцією між об’єктами. Наприклад, якщо два процеси та , задовольняють співідношенню виду 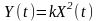, то кажуть, що між ними має місце нелінійний функціональний квадратичний зв’язок. У цьому разі, якщо в перерізі набуває значення , то процес у цьому ж перерізі набуде значення 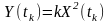з умовною ймовірностю 1. Тобто така подія є завжди достовірною і відбудеться обов’язково.

Під час оцінювання статистичного зв’язку в якості його верхньої межі беруть лінійну функціональну залежність між випадковими величинами або миттєвими значеннями процесів: 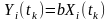. Вважається, що кореляція (ймовірний зв’язок) є сильною (гранично повною) за умови лінійного зв’язку між випадковими об’єктами.

Об’єкти некорельовані або коли статистичний зв’язок зовсім відсутній, або за наявності функціонального зв’язку, що істотно відрізняється від лінійного. Ось чому статистично незалежні величини (процеси) є некорельованими, водночас, некорельовані величини (процеси) не обов’язково є статистично незалежними.

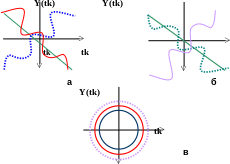
Рисунок 6.2 - Випадкові величини з додатньою (а), від’ємною