Лекція 1 Математична модель випадкового процесу.

Визначення випадкового процесу (ВП). Математична модель ВП. Випадкова функція. Вибіркова функція та статистичний ансамбль. Переріз ВП. Неперервні, дискретні та змішані ВП. Випадковий процес як система випадкових величин.

Література [ 3, с. 10-11. 12;с.7-1

Математична модель випадкового процесу

Процеси можна описати точно визначеними функціями часу та/чи просторової координати. Тоді характер розвитку процесу в майбутньому можливо завбачити достовірно, а його миттєві значення для будь-яких моментів часу точно визначити. Це процеси із наперед відомими характеристиками та параметрами і називаються вони детермінованими.

Фактично, жоден реальний процес не задовольняє зазначене. Неможливо задати достатню кількість параметрів, котра б описувала реальний процес як достовірну подію. За своєю природою вони випадкові. Це означає, що якщо багатократно спостерігати випадковий процес, то кожного разу він буде протікати по-іншому. До таких процесів, перш за все можна віднести процеси, пов’язані з передаванням та прийманням повідомлень, діями завад, мікроскопічними флуктуаційними явищами в елементах технічних об’єктів тощо.

Прикладами таких процесів можна вважати:

• випромінювані передавачем коливання;

• власні шуми приймальних пристроїв;

• атмосферні, індустріальні завади;

• електричні сигнали каналів зв’язку, які випадковим чином змінюються внаслідок взаємного впливу каналів.

Все це процеси, не наділені абсолютно незмінними параметрами. Ось чому, випадковий процес описується так званою випадковою функцією, значення якої є випадковими величинами і, отже, точно завбачені бути не можуть.

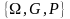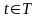Нехай - деякий імовірнісний простір, , , де - часовий скінченний чи нескінченний інтервал, 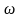- елементарна подія з множини елементарних подій , - ймовірнісна міра, що задана на множинах випадкових подій .

Функція двох аргументів , яка для кожного фіксованого моменту часу 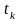є випадковою величиною на ймовірнісному просторі , а для фіксованого 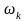є звичайною невипадковою функцією аргументу називається випадковою функцією.

Визначена у зазначений спосіб випадкова функція і є математичною моделлю випадкового процесу.

Підкреслимо, що в якості аргументу випадкової функції може бути не тільки час, а і об’єм, вага, площа, відстань, частота, тощо. Так, наприклад, товщина нитки є випадковою функцією відстані до її кінця.

Конкретна невипадкова функція, яка описує випадковий процес для фіксованого (у одному досліді, під час одного спостереження), називається реалізацією випадкового процесу або вибірковою функцією.

Зрозуміло, що в результаті проведення різних дослідів, навіть за однакових умов, ми отримаємо різні реалізації випадкового процесу.

На відміну від випадкового процесу, реалізацію ми можемо зобразити графічно, записати в пам’ять, наприклад ЕОМ, тощо.

Повна сукупність всіх можливих реалізацій випадкового процесу називається статистичним ансамблем. Наприклад, таким ансамблем є набір сигналів, які можливо одночасно спостерігати на виходах повністю однакових генераторів напруги. Або послідовність радіоімпульсів на вході радіолокатора, коли їхні параметри випадково змінюються із зміною умов розповсюдження імпульсів.

У подальшому, якщо не буде обумовлене інше, вважатимемо випадкову функцію та її реалізації функціями одного аргументу t. Довільну випадкову функцію позначатимемо великими буквами латинського алфавіту X(t), Y(t), Z(t) із вказуванням аргументу t в дужках, а їх відповідні окремі реалізації – малими буквами x_i(t), y_i(t), z_i(t) з індексом знизу, що відображає номер реалізації.

Отже, випадковий процес можна розглядати або як сукупність його реалізацій

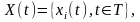(1.1)

або як сукупність випадкових величин 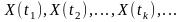(выбыркових значень) для будь-якої множини значень 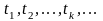(вибіркових моментів)

Н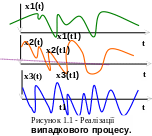 а рис. 6.1 наведено ансамбль із трьох реалізацій довільного випадкового процесу. Ці реалізації мають неперервну (без стрибків) структуру. Вони набувають будь-яких значень у межах заданої області можливих значень функції та можуть бути визначені для будь-якого значення аргументу t. Таке є визначальним для неперервних випадкових процесів

У разі, якщо миттєві значення процесу є величинами дискретними, набувають строго визначених, і ніяких інших, відлікових значень, процеси називаються дискретними.

Наприклад, напруга на виході реле, яка випадковим чином набуває значення 0 або 100 В залежно від того замкнені чи розімкнені контакти реле. Одна з можливих реалізацій дискретного випадкового процесу зображена на рис. 6.2.

П ідкреслимо, що зовсім не обов’язково, щоб конкретні реалізації випадкового процесу відображались функціями з дуже складною, нерегулярною в часі поведінкою.

Так, наприклад, гармонічне коливання 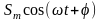, у якого один із трьох параметрів 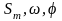є випадковою величиною, що набуває конкретного значення в окремій реалізації. Випадковий характер такого коливання зумовлений неможливістю апріорі завбачити значення цього параметру.

Зупинимось на такому понятті як переріз випадкового процесу. На рис. 6.1 на відстані t₁ від початку координат проведемо вертикальну пряму та відмітимо точки її перетину з реалізаціями x₁(t), x₂(t), x₃(t) процесу . Ординати цих точок – x₁(t₁), x₂(t₁), x₃(t₁) – миттєві значення процесу в момент часу t₁.

Таку сукупність миттєвих значень у довільний момент часу називатимемо перерізом випадкового процесу:

.

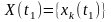Слід зазначити, що X(t₁) є випадковою величиною – дискретною або неперервною чи змішаною залежно від структури (характеру) випадкового процесу.

Лекція 2. Закони розподілу ймовірностей.

Ймовірнісні характеристики ВП. Інтегральний закон розподілу ймовірностей 1-го, 2-го та n-го порядків: визначення та основні властивості. Особливості функції розподілу ймовірностей неперервних, дискретних та змішаних процесів. Застосування ступінчастих функцій для опису законів розподілу..

Диференціальний закон розподілу ймовірностей 1-го, 2-го та n-го порядків: визначення та основні властивості. Особливості функції щільності ймовірностей неперервних, дискретних та змішаних процесів. Застосування функцій Дірака для опису диференціальних законів. Одно-, двох- та n-мірний елемент ймовірності, його графічна інтерпретація. Взаємозв'язок інтегрального та диференціального законів розподілу ймовірностей.

Література [3, с. 12-41; 41-80; 7, с. 76-89, с. 101-104; 9, с. 166-181; 1, 5 ].

Завдання на СРС. Характеристична функція: визначення, властивості та зв'язок з функцією щільності ймовірностей

1.Закони розподілу випадкових процесів процесів

Розглянемо ряд перерізів деякого випадкового процесу в 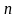точках (рис. 2.1), відстань між якими будемо вважати різною. Кожному перерізу t_k відповідає випадкова величина X(t_k), яку можна описати такими ймовірнісними характеристиками, як одновимірна функція розподілу ймовірностей та одновимірна функція щільності ймовірностей.

Очевидно, що в різних перерізах ці функції, в загальному випадку, будуть різними. Випадковий процес у цьому разі можна охарактеризувати випадковою величиною, що змінює свої ймовірнісні властивості зі зміною аргументу t. Однак слід враховувати, що миттєві значення процесу в сусідніх перерізах (якщо відстань між ними невелика) в якійсь мірі залежать одне від одного. Тобто, конкретне значення в одному перерізі визначає з деякою ймовірністю наступне (сусідне). Отже, випадковий процес на інтервалі [t₁, t_n] можна оцінювати системою із 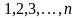випадкових величин, для яких встановлені відповідні ймовірнісні характеристики з урахуванням зв’язку між випадковими величинами в різних перерізах. Тоді йдеться про одновимірні, двовимірні, тривимірні, …, n – вимірні ймовірнісні характеристики (закони розподілу) випадкового процесу.

2. Одновимірні інтегральний та диференціальний закони розподілу

Такі закони є ймовірнісними характеристиками випадкового процесу відносно одного перерізу і характеризують процес у статиці.

Інтегральний закон. Припустімо, що в момент часу t_k переріз процесу визначається випадковою величиною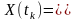 . Крім того, зафіксуємо деякий рівень X_k можливих миттєвих значень процесу X(t). Очевидно, що для заданого ансамблю деякі реалізації в точці t_k набудуть значень, які перевищать X_k, а інші – що будуть меншими за X_k. При зміні рівня X_k, наприклад, на X_k+1, зміниться і кількість реалізацій, які в точці t_k перевищують цей рівень. Цікаво б було знати: наскільки ймовірно, що всі реалізації випадкового процесу набудуть в точці t_k значень, менших за вибраний рівень X_k. На це і дає відповідь одновимірний інтегральний закон розподілу ймовірностей випадкової величини або одновимірна функція розподілу

F₁(X_k, t_k).

Функція розподілу ймовірностей F₁(X_k, t_k) визначає ймовірність того, що випадкова величина X(t_k) в перерізі t_k набуває значень, які не перевищують рівень X_k:

(2.1)

Таким чином, згідно з (2.1) для заданого рівня X_k1 всі реалізації випадкового процесу X(t) із ймовірністю F₁(X_k1, t_k) перетнуть переріз у точці t_k нижче X_k1 або на цьому рівні (рис. 2.2, а).

Рисунок 6.4 - До визначення одновимірної функції розподілу ймовірностей.

На рис. 2.2, б показана одна із можливих функцій розподілу випадкового процесу, реалізації якого в перерізі не перевищують рівня X_k1 з ймовірністю F₁(X_k1, t_k). Слід зазначити, що одновимірна функція розподілу є функцією одного аргументу X_k, а величина є її параметром.

Основні властивості одновимірної функції розподілу:

• F₁(X_k, t_k) – невипадкова функція дійсного аргументу X_k;

• F₁(X_k = - ймовірність того, що випадкова величина в будь-який момент часу набуває значення, яке не перевищує мінус нескінченність, дорівнює нулю;

• F₁(X_k = 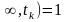- подія, за якої значення випадкової величини будуть завжди меншими нескінченності, є достовірною;

• F₁(X_k, t_k) є неспадною функцією, значення якої лежать в межах [0, 1] і при

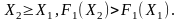
Рисунок 2.3 - Одновимірна функція розподілу ймовірностей