4.Вычислите объём тела ограниченного поверхностями:

П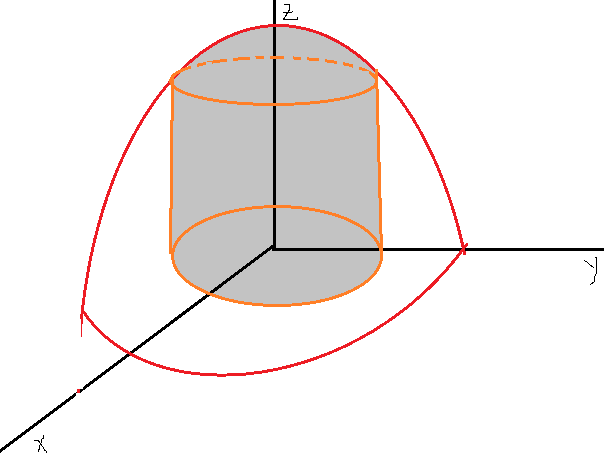 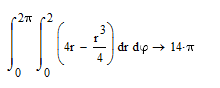ересечение:

V=

5. Используя формула стокса вычислите циркуляцию векторного поля по контуру треугольника авс с заданными вершинами a(1;1;0), b(0,0,2), c(3,0,1).

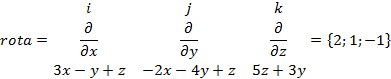
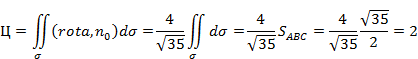
6.Фурье Билет 12.

1 Вопрос) Циркуляция векторного поля. Циркуляцией называется линейный интеграл векторного поля по замкнутой кривой С: .

Обычно говорят, что циркуляция характеризует вращательную способность поля. Имеется в виду следующее. Если векторные линии поля замкнуты, то, как мы видели, циркуляция по ним в направлении поля положительна, при этом в гидродинамической интерпретации частицы жидкости крутятся по этим замкнутым линиям.

Ротор векторного поля. Ротором векторного поля (M) в точке называется векторная величина (векторное поле) = .

.

Смысл Ротора – характеризует закручивающую способность поля.

2 Вопрос) Определение единичного вектора нормали к поверхности. Выражения для элемента площади поверхности. Предположим, что поверхность задаётся неявным уравнением ( - непрерывно дифференцируемая функция) и взаимно однозначно проецируется в область на плоскости Оху. , где знак перед дробью соответствует возможности выбора двух возможных взаимно противоположных направлений нормали. В координатной форме , то , , 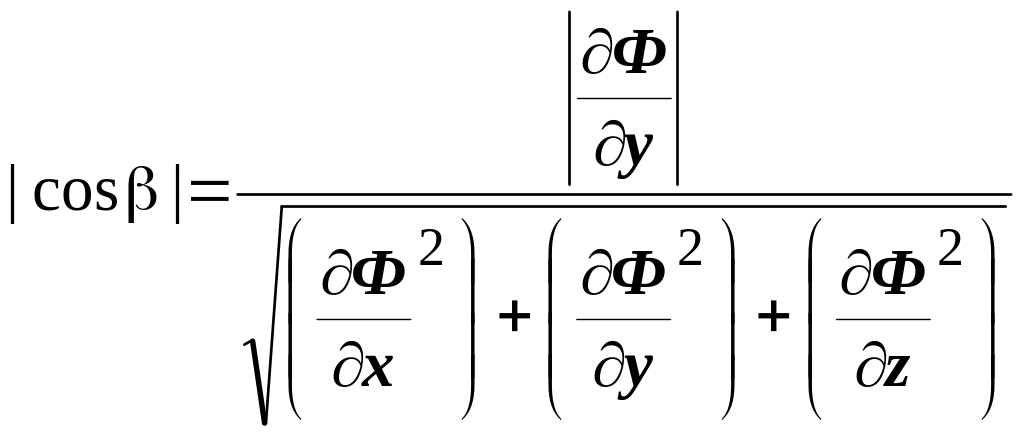. Теперь мы можем выразить элемент площади поверхности через элемент площади в каждой координатной плоскости: , , .

Выражение поверхностного интеграла через двойной интеграл по проекции поверхности на координатную плоскость. Пусть поверхность взаимно однозначно проецируется в область на плоскости Оху. Будем считать, что поверхность задана уравнением , . В интегральной сумме выразим площадь через двойной интеграл по её проекции на плоскость Оху: . Применим к этому интегралу теорему о среднем: существует точка такая, что . Значение подынтегральной функции будем вычислять в точке , такой, что . Тогда .

.

3 Вопрос)фурье

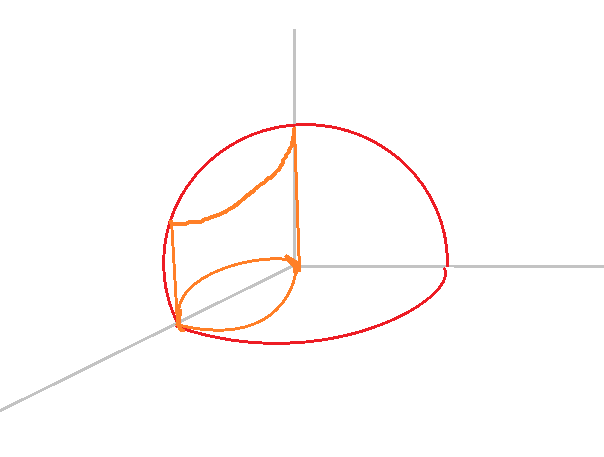
4.Вычислите массу части оболочки полусферы , вырезанной цилиндром , если плотность оболочки

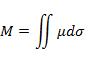
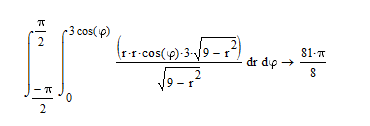
5.Вычислите поток векторного поля через замкнутую поверхность тела, определяемую неравенствами

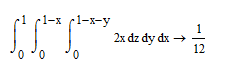
6. Найдите область сходимости ряда

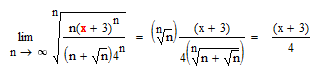
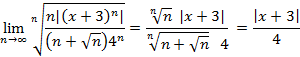
На граничных точках

Билет №13

1. Дивергенция. Физический смысл. Источники и стоки.

Дивергенция – характеристика векторного поля, характеризующее распределение и интенсивность источников и стоков поля.

Дивергенцией (или расходимостью) векторного поля

в точке M называется скаляр вида и обозначается символом , т.е.

Свойства дивергенции:

1. Если – постоянный вектор, то

2. 

3. 

4. Если 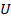- скалярная функция, –вектор, то

Дивергенцией векторного поля в точке M называется предел отношения потока через замкнутую поверхность S, окружающую точку M, к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку M

Дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном.

Исходя из физического смысла потока(обычно условно считают, что есть поле скоростей фиктивного стационарного потока несжимаемой жидкости) можно сказать, что при точка M представляет собой источник, откуда жидкость вытекает; при точка M есть сток, поглощающий жидкость. Величина характеризует мощность источника или стока в точке M. В этом и состоит физический смысл дивергенции. При векторное поле называется соленоидальным, а это означает что в объеме нет ни стоков, ни источников(либо они компенсируются).