18.1.2. Свойства потенциального поля.

1. Потенциал определён с точностью до произвольной постоянной ( ).

2. 2. Разность потенциалов в двух точках определена однозначно.

3. Если поле (M) потенциально, то линейный интеграл этого поля по любой кривой , целиком лежащей в V, определяется только начальной и конечной точками этой кривой, и не зависит от формы кривой. . Эта формула, как и в плоском случае, является обобщением формулы Ньютона-Лейбница для потенциального поля.

4. Циркуляция потенциального в области V поля по любому контуру, лежащему в V, равна нулю.

5. Векторная линия потенциального поля в каждой точке М ортогональна эквипотенциальной поверхности ( т.е. поверхности уровня потенциала), проходящей через точку М.

6. Ротор потенциального векторного поля равен нулю:

.

Введём определение безвихревого поля: поле (M), ротор которого в каждой точке равен нулю, называется безвихревым.

Мы доказали, что потенциальное поле необходимо безвихрево.

Линии равного потенциала(Эквипотенциальная поверхность )

Эквипотенциальная поверхность — это поверхность, на которой скалярный потенциал данного потенциального поля принимает постоянное значение (поверхность уровня потенциала). Другое, эквивалентное, определение — поверхность, в любой своей точке ортогональная силовым линиям поля.

Эквипотенциальные поверхности это такие поверхности каждая из точек, которых обладают одинаковым потенциалом. То есть на эквипотенциальной поверхности электрический потенциал имеет неизменное значение. Такой поверхностью является поверхности проводников, так как их потенциал одинаков.

Представим себе такую поверхность, для двух точек которой разность потенциалов будет равна нулю. Это и будет эквипотенциальная поверхность. Поскольку потенциал на ней одинаков. Если рассматривать эквипотенциальную поверхность в двухмерном пространстве, допустим на чертеже, то она будет иметь форму лини. Работа сил электрического поля по перемещению электрического заряда вдоль этой лини будет равна нулю.

Одним из свойств эквипотенциальных поверхностей является то, что они всегда перпендикулярны силовым линиям поля. Это свойство можно сформулировать и наоборот. Любая поверхность, которая перпендикулярна во всех точках к линиям электрического поля и называется эквипотенциальной.

Также такие поверхности никогда не пересекаются между собой. Так как это означало бы различие потенциала в пределах одной поверхности, что противоречит определению. Еще они всегда замкнуты. Поверхности равного потенциала не могут начаться и уйти в бесконечность, не имея при этом четких границ.

Примеры потенциальных полей:

1)поле тяготения точечной массы м,2)поле электрического точечного заряда е.

4)

5)

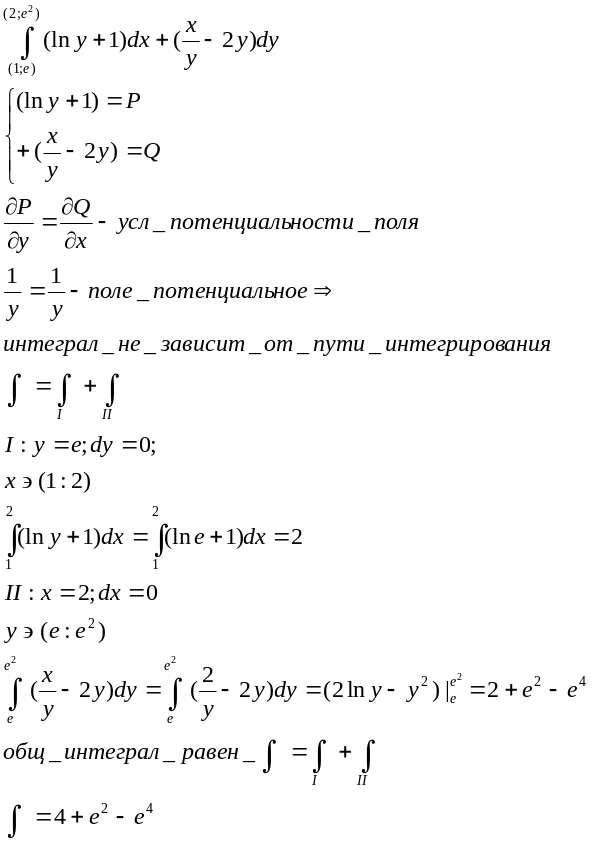
6)

Билет 27

1 .Определение тройного интеграла. Пусть в пространстве Oxyz задана ограниченная замкнутая область (объём) V, и пусть на области V определена функция .

Разобьём область V произвольным образом на подобластей (не имеющих общих внутренних точек). Символом будем обозначать объём области ; символом обозначим наибольший из диаметров областей : .

В каждой из подобластей выберем произвольную точку , вычислим в этой точке значение функции , и составим интегральную сумму .

Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения области V на подобласти , ни от выбора точек , то функция называется интегрируемой по области V, а значение этого предела называется тройным интегралом от функции по области V и обозначается .

Если расписать значение через координаты точки , и представить как , получим другое обозначение тройного интеграла: . Итак, кратко, .

17. В ычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному. Будем называть ограниченную замкнутую область V простой (правильной), если выполняются два условия : проекция V на какую-либо координатную плоскость, например, на плоскость Оху - простая область D, и любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку V, пересекает границу V в двух точках. Такую область можно описать следующим образом: (поверхность образована множеством нижних точек пересечения прямой, параллельной оси Oz, с границей V; поверхность 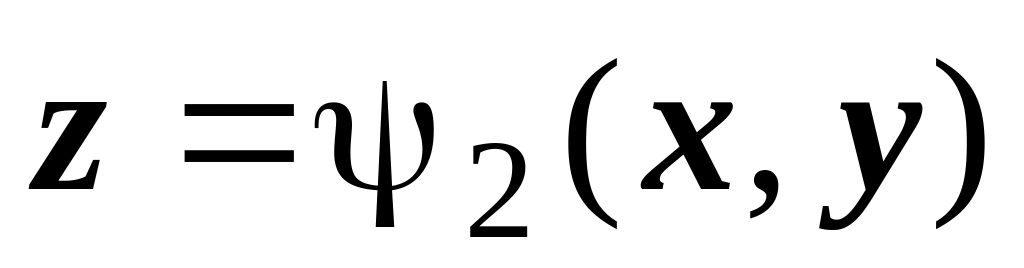- множеством верхних точек пересечения).

Теорема. Если V - простая область с кусочно-гладкой границей, - непрерывная функция, то .

Пример

Проекция области V на плоскость Оху - треугольник , поэтому

.

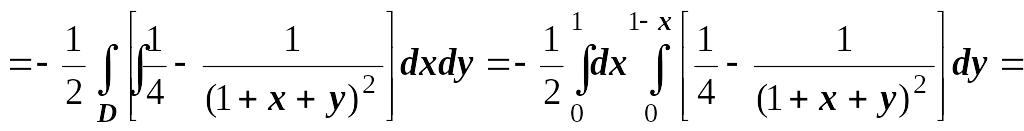
2 . Выражение поверхностного интеграла через двойной интеграл по проекции поверхности на координатную плоскость. Пусть поверхность взаимно однозначно проецируется в область на плоскости Оху. Будем считать, что поверхность задана уравнением , . В интегральной сумме выразим площадь через двойной интеграл по её проекции на плоскость Оху: . Применим к этому интегралу теорему о среднем: существует точка такая, что . Значение подынтегральной функции будем вычислять в точке , такой, что . Тогда .

Слева стоит интегральная сумма для поверхностного интеграла, справа - для двойного; переход к пределу при (при этом и ) даёт

.

Эта формула и применяется для вычисления поверхностных интегралов. Естественно, в каждой задаче надо выбирать, на какую из координатных плоскостей предпочтительней проецировать поверхность; если проецирование не взаимно однозначно, поверхность разбивается на части, которые проецируются однозначно.

Пример

Найти , где  - сфера x² + y² + z² = R².

Решение: Использование соображений симметрии позволяет иногда существенно упростить вычисление интегралов. Очевидно, что для сферы . Тогда

3. .

Воспользуемся тем, что . Так как , то, после почленного интегрирования,

.

Область сходимости этого ряда - полуинтервал , сходимость к функции во внутренних точках следует из теоремы о почленном интегрировании степенного ряда, в точке х=1 - из непрерывности и функции, и суммы степенного ряда во всех точках, сколь угодно близких к х=1 слева. Отметим, что взяв х=1, мы найдём сумму ряда .

4)

5)

6)

А)

Б)

Билет 28

1.Теорема Стокса. Пусть в пространственной области V задано гладкое векторное поле

(M) и - незамкнутая кусочно-гладкая поверхность, ограниченная контуром С. Единичный вектор нормали выбирается так, что с его конца направление обхода С видно совершающимся против часовой стрелки. Тогда циркуляция поля по контуру С равна потоку ротора этого поля через поверхность : .

Приведённую формулу называют формулой Стокса в векторной форме. В координатной форме формула Стокса имеет вид

или

Говорят, что циркуляция характеризует вращательную способность поля. Вообразим в объёме V замкнутый контур С. Если в результате движения жидкости этот контур будет вращаться, то поле обладает вращательной способностью; абсолютная величина циркуляции будет определять угловую скорость вращения (чем больше |Ц|, тем выше скорость); знак циркуляции покажет, совпадает ли направление вращения с направлением интегрирования.

Ротор характеризует вращательную способность в единице площади. Представить ротор можно как вытекающую в трубу воду, поле скоростей воды всегда имеет вид циркуляции, ротор этого поля практически нигде не будет равен нулю.

2.Теорема Грина для односвязной области. Пусть на плоскости Oxy задана односвязная область D, ограниченная кусочно-гладким контуром C. На множестве определены непрерывные функции и , имеющие непрерывные частные производные. Тогда , при этом контур С обходится так, что область D остаётся слева.

Док-во. 1. Пусть D - простая область. Докажем сначала, что . О пишем D неравенствами Тогда . Если контур включает вертикальные участки, такие как EF, то на этих участках dx= 0, поэтому , и , что и требовалось доказать.

Равенство доказывается точно также: . Суммируя равенства и , получим одну из важнейших формул анализа -формулу Грина

3. Признак сходимости Даламбера. Пусть для положительного ряда существует . Тогда

если q<1, то ряд сходится,

если q >1, то ряд расходится,

если q=1, то ряд может и сходиться, и расходиться.

Доказательство. 1. Пусть <1. Возьмём . . Если q<1, то число . Итак, при . Выпишем это неравенство для : , , , … , . Все члены ряда, начиная с N+2-го, меньше членов сходящейся геометрической прогрессии, поэтому сходится, поэтому сходится.

2. Пусть >1. Возьмём . .

Если q>1, то число . Итак, при . Выпишем это неравенство для : , , , … , . Все члены ряда, начиная с N+2-го, больше членов расходящейся геометрической прогрессии, поэтому расходится, поэтому расходится.

3. Для рядов и мы опять получим q =1. Первый из этих рядов сходится, второй расходится, но для обоих q=1, т.е. в этом случае вопрос о сходимости ряда действительно остаётся открытым.

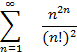
4. Изменить порядок интегрирования и перейти к полярным координатам.

+

5. Вычислить координату центра тяжести Xc плоскости z=x, ограниченной плоскостями x+y=1, x=0, y=0, µ(x,y,z)=1

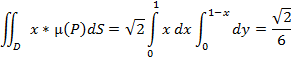
Xc=

6. Найти интервал сходимости ряда

Знакочередующийся ряд, рассмотрим ряд из модулей

Коши радикальный

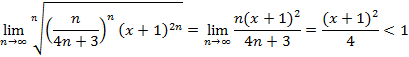
Радиус сходимости равен 2, x

Рассмотрим левую грницу при х=-3

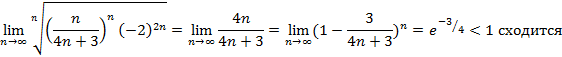
Рассмотрим правую границу при х=1

Ответ: х

Билет 29

1. . Теорема о замене переменных в тройном интеграле. Пусть в пространстве Ouvw задана область G, и пусть отображение преобразует эту область в область V пространства Oxyz. Будем считать, что отображение F задаётся функциями . Пусть: 1). F взаимно однозначно отображает G на V; 2). Функции x(u,v,w), y(u,v,w), z(u,v,w) непрерывно дифференцируемы на G (имеют непрерывные частные производные); 3). Якобиан не обращается в нуль на G. Тогда .

Здесь область интегрирования - шар радиуса 1/2, сдвинутый по оси Оz на 1/2 единицы, подынтегральная функция зависит от выражения x ² + y ² + z ², поэтому применим сферические координаты. Уравнение сферы , поэтому

2. . Определение криволинейного интеграла первого рода. Пусть в пространстве переменных x,y,z задана кусочно-гладкая кривая , на которой определена функция f(x,y,z). Разобьём кривую точками на частей, на каждой из дуг выберем произвольную точку , найдём и длину дуги , и составим интегральную сумму . Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения кривой на дуги , ни от выбора точек , то функция f(x,y,z) называется интегрируемой по кривой , а значение этого предела называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги от функции f(x,y,z) по кривой , и обозначается (или ).

Криволинейный интеграл I рода обладает следующими свойствами:

1. Интеграл не зависит от ориентации кривой;

2. Пусть кривая C₁ начинается в точке A и заканчивается в точке B, а кривая C₂ начинается в точкеB и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться криваяC₁ U C₂, которая проходит от A к B вдоль кривой C₁ и затем от B к D вдоль кривой C₂. Для криволинейных интегралов первого рода справедливо соотношение

3. Если гладкая кривая C задана параметрически соотношением 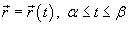  и скалярная функция F непрерывна на кривой C, то

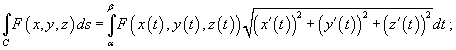
4. Если C является гладкой кривой в плоскости Oxy, заданной уравнением 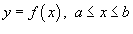 , то

5. Если гладкая кривая C в плоскости Oxy определена уравнением 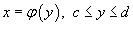 , то

6. В полярных координатах интеграл 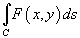  выражается формулой

Механические приложения

Масса m материальной кривой с плотностью (x,y,z) вычисляется по формуле .

Статические моменты и координаты центра масс. Пусть плоская материальная кривая имеет плотность (x,y). Статический момент относительно оси Ox определяется по формуле , относительно оси Oy: .

- для плоской кривой;

Моменты инерции. Моменты инерции плоской кривой с плотностью  относительно координатных осей вычисляются по формулам

,

моменты инерции относительно начала координат

В случае пространственной кривой моменты инерции относительно координатных осей и начала координат определяются по формулам

, , ,

3. Достаточный признак сходимости знакочередующегося ряда (признак Лейбница). Если

1. Последовательность, составленная из модулей членов знакочередующегося ряда, монотонно убывает, т.е. ;

2. Выполняется необходимый признак сходимости ряда, т.е. ,

то ряд сходится. Его сумма по абсолютной величине не превосходит абсолютную величину первого члена.

Доказательство. Рассмотрим последовательность чётных частичных сумм ряда. Представим эту сумму в виде . Из первого условия теоремы следует, что суммы в круглых скобках неотрицательны, поэтому последовательность монотонно возрастает с ростом n. С другой стороны, , т.е. эта последовательность ограничена сверху величиной . Следовательно . Но для нечётных сумм , так как по второму условию теоремы . Таким образом, частичные суммы имеют предел независимо от их четности или нечётности, т.е. ряд сходится, и его сумма . Знак суммы совпадает со знаком первого члена.

Правило оценки:

Если ряд знакочередующийся, то сначала рассматривают его на абсолютную сходимость, то есть ряд из модулей, если абсолютной сходимости нет, то ряд рассматривают на условную сходимость.

4. Вычислить криволинейный интеграл второго рода

L:

По формуле Грина

Т.к. наш контур эллипс, то используем обобщенные полярные координаты x=a

Y=b

Якобиан равен I=abr

5.Вычислить массу тела, ограниченного поверхностями z=0, z=y, y=

Если плотность

M= модуль сняли в силу симметрии фигуры и рассмотрели область х>0 y>0

6 Найдите интервал сходимости степенного ряда

По Даламберу <1

Радиус сходимости равен 1, интервал сходимости x -3;-1). Исследуем ряд на границах интервала сходимости

Знакочередующийся ряд, исследуем на абсолютную сходимость ряд из модулей

;

Аналогично для правой границы, ряд на правой границе сходится

Ответ x

Билет 30.

1. Дайте определение несобственного двойного интеграла 2-го рода с особенностью в изолированной точке. Приведите примеры сходящихся и расходящихся интегралов.

Логика определения сходимости несобственного двойного, тройного, n - кратного интеграла по неограниченной области такая же, как и для несобственного определённого интеграла: мы ограничиваем область, вычисляем интеграл по этой ограниченной области, и, затем, расширяя область интегрирования до исходной, смотрим, существует или нет конечный предел значения интеграла. Рассмотрим это более подробно для случая двойного интеграла.

Пусть в неограниченной области D определена функция f(x, y). Построим бесконечную последовательность ограниченных областей G_i, i = 1,2,…, удовлетворяющую следующим условиям:

1. ,

16. 2. ,

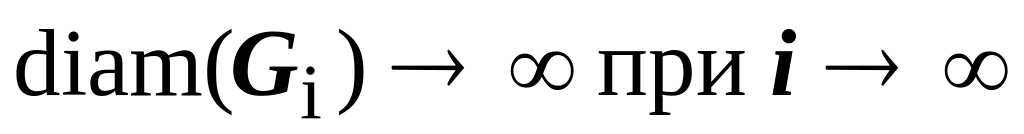17. 3. для любой точки существует такой номер i₀, что при .

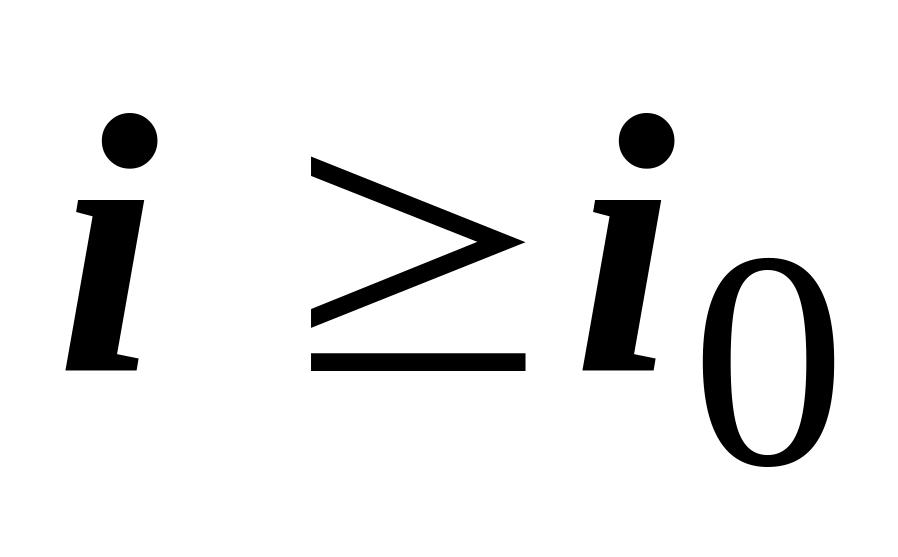П усть теперь . Любая такая область ограничена. Рассмотрим последовательность значений интегралов . Если для любой последовательности существует конечный , то несобственный интеграл называется сходящимся, а значение предела - значением этого интеграла; если хотя бы для одной последовательности не существует или бесконечен, несобственный интеграл называется расходящимся.

Несобственные интегралы от неограниченной функции. Структура множества точек, в окрестностях которых функция двух, трех и большего числа переменных может оказаться неограниченной, может быть достаточно сложной. Так, функция трёх переменных может быть неограниченной в окрестности одной точки , прямой , плоскости ; естественно, возможны более сложные случаи. Мы рассмотрим самый простой случай, когда функция неограничена в окрестности единственной точки.

Пусть функция двух переменных f(x, y) определена и непрерывна в ограниченной замкнутой области D всюду, за исключением точки P₀. Возьмём бесконечную последовательность ограниченных областей G_i, i = 1,2,…, удовлетворяющую следующим условиям:

1. ,

16. 2. ,

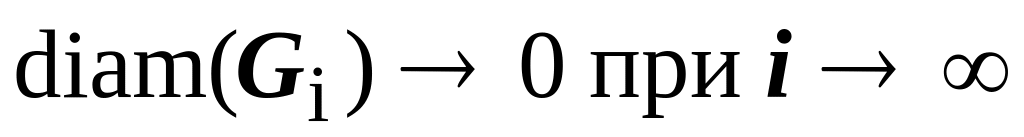Пусть теперь . В каждой такой области функция f(x, y) непрерывна. Рассмотрим последовательность значений интегралов . Если для любой последовательности существует конечный , то несобственный интеграл называется сходящимся, а значение предела - значением этого интеграла; если хотя бы для одной последовательности не существует или бесконечен, несобственный интеграл называется расходящимся.

И в этом случае можно показать, что:

1. если подынтегральная функция сохраняет знак на области D, то для сходимости достаточно существования конечного 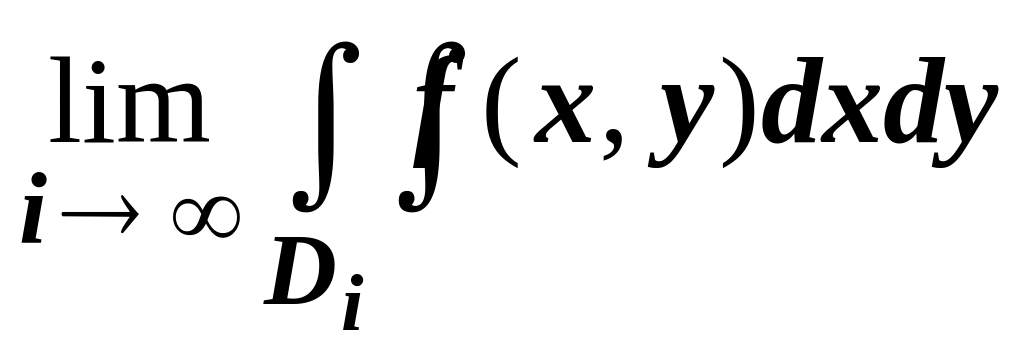для какой-либо одной последовательности .

2. Для таких функций справедливы признаки сравнения.

3. Если сходится , то обязательно сходится и

Пример. . Здесь область D - внутренность круга радиуса 1. Выберем последовательность (круги радиуса 1/i), тогда - кольцо , и ( ) . Это выражение имеет конечный предел при , если p < 2. Случай p = 2 исследуется отдельно и приводит к расходимости. Таким образом, исследуемый интеграл сходится при p < 2.

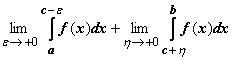Особенность во внутренней точке промежутка интегрирования. Пусть функция f(x) определена на отрезке [a, b], имеет бесконечный предел при стремлении аргумента к какой-либо внутренней точке c этого отрезка:  , интегрируема по любому отрезку, не содержащему точку c. Несобственным интегралом от f(x) по отрезку [a, b] называется . Интеграл сходится, если оба эти пределы существуют и конечны, в противном случае интеграл расходится.

Несколько особенностей на промежутке интегрирования. Этот случай сводится к предыдущим. Пусть, например, функция имеет бесконечные пределы при стремлении аргумента к внутренним точкам c₁, c₂, c₃ отрезка [a, b] (a < c₁ < c₂ < c₃ < b) и правому концу b, и интегрируема по любому отрезку, не содержащему эти точки. Тогда несобственный интеграл определяется как  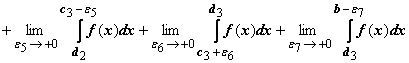  . Здесь d₁, d₂, d₃ - произвольные точки, удовлетворяющие неравенствам a < c₁ < d₁ < c₂ < d₂ < c₃ < d₃ < b.  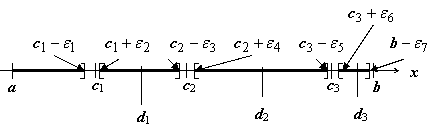Пример: 21.     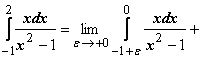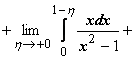, и интеграл расходится, так как все три предела бесконечны. Решение с применением формулы Ньютона-Лейбница: 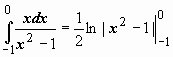  - расходится, так как первообразная   обращается в бесконечность в точке x = -1.

2. Потенциальное векторное поле и его свойства. Вычисление криволинейного интеграла в векторном поле.

Определение потенциального поля. Векторное поле (M) называется потенциальным в области V, если существует такое скалярное поле , что (M) для . Поле называется потенциалом поля (M).

Свойства потенциального поля.

1. Потенциал определён с точностью до произвольной постоянной ( ).

2. 2. Разность потенциалов в двух точках определена однозначно.

3. Если поле (M) потенциально, то линейный интеграл этого поля по любой кривой , целиком лежащей в V, определяется только начальной и конечной точками этой кривой, и не зависит от формы кривой. . Эта формула, как и в плоском случае, является обобщением формулы Ньютона-Лейбница для потенциального поля.

4. Циркуляция потенциального в области V поля по любому контуру, лежащему в V, равна нулю.

5. Векторная линия потенциального поля в каждой точке М ортогональна эквипотенциальной поверхности ( т.е. поверхности уровня потенциала), проходящей через точку М.

6. Ротор потенциального векторного поля равен нулю:

.

Введём определение безвихревого поля: поле (M), ротор которого в каждой точке равен нулю, называется безвихревым.

Мы доказали, что потенциальное поле необходимо безвихрево. Дальше мы займёмся достаточными условиями потенциальности.

Достаточные условия потенциальности.

Теорема. Если область V и поле (M) удовлетворяют следующим условиям:

1. V - односвязная область;

2. Поле (M) - безвихрево (т.е. ),

то (M) - потенциальное в V поле.

Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути. Именно, требуется доказать, что . Действительно, пусть

. Тогда ,

(на ) (по теореме о среднем) . Точка удовлетворяет условиям . Устремим , тогда , и .

Аналогично доказывается, что .

Задача 4.

Найдите площадь части поверхности сферы x²+y²+z²=a², заключенной внутри цилиндра x²+y²=ax

Решение:

.

z= √(a²-(x²+y²))

z^’_x= - x/√(a²-(x²+y²));

z^’_y= - y/√(a²-(x²+y²));

s(σ) = ∫∫√(1+x²/(a²-(x²+y²))+y²/(a²-(x²+y²))) dxdy= a ∫∫( 1/√(a²-(x²+y²))) dxdy = a ∫ dφ (пределы инт. От –π/2 до π/2) ∫ (1/√(a²-r²)) dr(от 0 до a) = a ∫ dφ (пределы инт. От –π/2 до π/2) * arcsin(r/a) (от 0 до a) = aπ²/2

Задача 5

Применяя формула Стокса, вычислите циркуляцию векторного поля a= (2x² + 4z) i + (x-3y+z) j + (3y-2)k по контуру треугольника с вершинами A(0;1;0), B(0;0;1), C(1;0;1), обход совершается в направлении ABCA

Решение

Ц = ;

n= {0;-1;-1};

n₀ = 1/√2{0;-1;-1};

rot a = {2;-4;1};

(rot a,n₀) =3/√2

Ц= ∫∫3/√2 dS= 3/√2* S_ABC=3/√2*0.5*√2=1.5

Задача 6.

Исследуйте числовые ряды на сходимость

a)∑ (-1)ⁿ/(n- ln n) n=2….беск.

|a_n|= 1/(n- ln n) ̴ 1/n(1-ln n/n) ̴ 1/n, но по критерию сходимости Коши 1/n – гармонический расходящийся ряд => ряд расходится.

б) ∑ tg((-1)ⁿ⁺¹π/2√n) ̴∑ (-1)ⁿ⁺¹π/2√n;

|a_n|= π/2√n= π/2n^1/2<1 => расходится