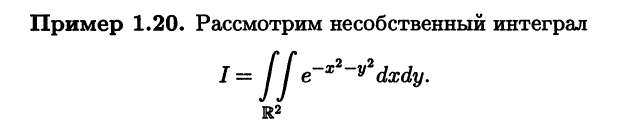Билет 1.
1. Теорема о среднем и об оценке двойного интеграла. Доказательство.
2. Поверхностный интеграл первого рода. Способ вычисления. Пример.
3. разложение в ряд Тейлора и Маклорена. разложение в ряд маклорена функции y=ex. докозательство.
Задание №4
Задание №5
n=(-3,0,0), n0=(-1,0,0) (нормировали)
a*n= 5-2x
x=3)=
=(интеграл
– площадь круга)=
Задача №6
а)
Лейбниц и признак сравнения:
Ряд 1/n – расходится. => Первоначальный ряд сходится условно и монотонно убывает.
б)
Лейбниц и Даламбер:
ряд расходится. => Исходный ряд условно сходится.
Билет 2.
1. Теорема о среднем и об оценке для тройного интеграла.
Док-во. Непрерывная на ограниченном
замкнутом объеме V функция
f(P) принимает
в некоторых точках этой области свое
минимальное m и максимальное
M значения. Так как m
≤ f(P) ≤ M,
то m·ν(V)≤
≤M·ν(V)
или
.
Непрерывная функция принимает, кроме
того, любое значение, заключенное мeжду
m и M, в
частности, значение
.
Следовательно,
такое
что
,
откуда и следует доказываемо утверждение.
Док-во.
m·ν(V)≤
≤M·ν(V)
2. Определение криволинейного интеграла второго рода. Способ его вычисления. Пример.
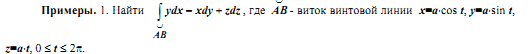
РАВНОМЕРНО СХОДЯЩИЙСЯ РЯД
функциональный ряд
с (вообще говоря) комплексными членами, сходящийся на множестве X, и такой, что для любого ɛ>0 существует номер nɛ , что для всех n > nɛ и всех выполняется неравенство
где
и
Иными словами, последовательн
ость
частичных сумм sin(х).является
равномерно сходящейся последовательностью.
Определение Р. с. р. равносильно выполнению
условия
что означает равномерную сходимость к нулю на множестве X последовательности остатков
ряда (1).
Пример. Ряд
равномерно сходится на каждом конечном круге комплексной плоскости и не сходится равномерно на всем множестве С комплексных чисел.
Условие равномерной сходимости ряда (1) на множестве X без использования понятия суммы ряда дает Ноши критерий равномерной сходимости ряда. Достаточное условие равномерной сходимости ряда дается Вейерштрасса признаком.
Ряд
наз. правильно сходящимся на множестве
X, если существует такой числовой ряд ,
что для всех n=1, 2,. . . и всех
выполняется неравенство
т. е. если ряд (1) удовлетворяет условиям признака Вейерштрасса равномерной сходимости рядов. В силу этого признака правильно сходящийся на множестве X ряд равномерно сходится на этом множестве. Обратное, вообще говоря, неверно; однако во всяком равномерно сходящемся на множестве X ряде можно так объединить следующие друг за другом его члены в конечные группы, что получившийся при этом ряд будет уже правильно сходиться на множестве X.
Задание №4
,
Задача №5
Билет 3.
1. Двойной несобственный интеграл. Интеграл Пуассона.
|
|
2. Определение криволинейного интеграла 1го рода. способ вычисления. Пример.
3. Докажите необходимый признак сходимости числового ряда.
Задача №4
через
дискриминант получаем, что
Задача №5.
Т. Стокса:
Для определения исключим из начальных уравнений x
Для определения исключим из начальных уравнений x
Задача №6
Напоминание
Билет 4
Тройной интеграл в цилиндрических координатах. В этой координатной системе положение точки в пространстве характеризуется тремя числами: r, и z, где r и - полярные координаты проекции M1
т
очки
М на плоскость Оху, z
- аппликата точки M.
Формулы перехода от цилиндрических
координат к декартовым:
Вычислим якобиан этого преобразования:
,
следовательно,
.
Тройной интеграл в сферических
координатах. В этих координатах
положение точки M
в пространстве характеризуется тремя
числами: r,
и
,
где r - длина
радиуса-вектора точки M,
-
полярный угол проекции M1
точки М на плоскость
Оху,
- угол между радиусом-вектором точки M
и осью Oz. Формулы
перехода от сферических координат к
декартовым:
Вычислим якобиан этого преобразования:
,
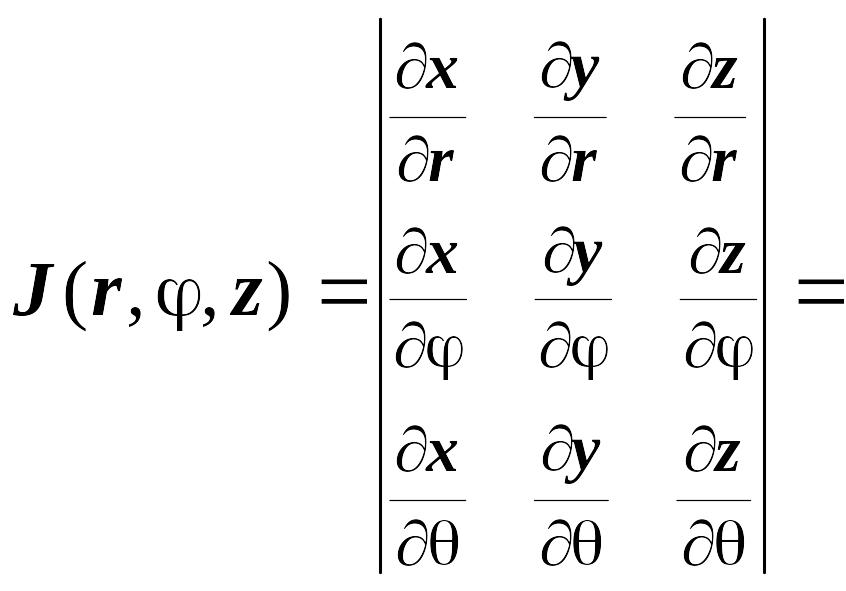
следовательно,
.
Формула Стокса:
Физический смысл формулы Стокса состоит
в том, что циркуляция векторного поля
вдоль замкнутого контура 
численно равна потоку ротора этого
поля через произвольную поверхность
,
натянутую на этот контур.
Физический смысл ротора.
Можно использовать представление о вращении брошенной в поток маленькой пылинки (увлекаемой потоком с собой, без его заметного возмущения) или о вращении помещённого в поток с закреплённой осью маленького (без инерции, вращаемого потоком, заметно не искажая его) колеса с прямыми (не винтовыми) лопастями. Если то или другое при взгляде на него вращается против часовой стрелки, то это означает, что вектор ротора поля скорости потока в данной точке имеет положительную проекцию в направлении на нас.
Обычно говорят, что циркуляция характеризует вращательную способность поля. Имеется в виду следующее. Если векторные линии поля замкнуты, то, как мы видели, циркуляция по ним в направлении поля положительна, при этом в гидродинамической интерпретации частицы жидкости крутятся по этим замкнутым линиям. Пусть теперь линии тока произвольны; вообразим в объёме V замкнутый контур С. Если в результате движения жидкости этот контур будет вращаться, то поле обладает вращательной способностью; абсолютная величина циркуляции будет определять угловую скорость вращения (чем больше |Ц|, тем выше скорость); знак циркуляции покажет, совпадает ли направление вращения с направлением интегрирования.
(-1;1)
Посчитать массу криво.
.
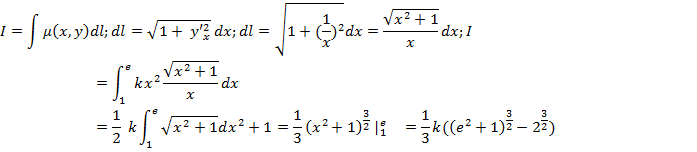
Посчитать циркуляцию поля с помощью формулы Стокса. Контур
Билет 5
Пусть на плоскости Oxy задана ограниченная замкнутая область D с кусочно-гладкой границей, и пусть на области D определена функция
.
Разобьём область D
произвольным образом на
подобластей
(не имеющих общих внутренних точек).
Символом
будем обозначать площадь области
;
символом
здесь и дальше будет обозначаться
наибольшее расстояние между двумя
точками, принадлежащими области D:
;
символом
обозначим наибольший из диаметров
областей
:
.
В каждой из подобластей
выберем произвольную точку
,
вычислим в этой точке значение функции
,
и составим интегральную сумму
.
Если существует предел последовательности
интегральных сумм при
,
не зависящий ни от способа разбиения
области D на
подобласти
,
ни от выбора точек
,
то функция
называется интегрируемой по области
D, а значение этого
предела называется двойным интегралом
от функции
по области D и
обозначается
.
Если
расписать значение
через координаты точки
,
и представить
как
,
получим другое обозначение двойного
интеграла:
.
Это и есть площадь.
Циркуляцией называется линейный интеграл векторного поля по замкнутой кривой С:
.
Обычно говорят, что циркуляция характеризует вращательную способность поля. Имеется в виду следующее. Если векторные линии поля замкнуты, то, как мы видели, циркуляция по ним в направлении поля положительна, при этом в гидродинамической интерпретации частицы жидкости крутятся по этим замкнутым линиям. Пусть теперь линии тока произвольны; вообразим в объёме V замкнутый контур С. Если в результате движения жидкости этот контур будет вращаться, то поле обладает вращательной способностью; абсолютная величина циркуляции будет определять угловую скорость вращения (чем больше |Ц|, тем выше скорость); знак циркуляции покажет, совпадает ли направление вращения с направлением интегрирования.
Ротором векторного поля
(M)
в точке
называется векторная величина (векторное
поле)
.
Запомнить эту формулу очень легко, если
выразить
через оператор Гамильтона набла:
равен векторному произведению
.
Действительно,
.
Если теперь раскрыть этот определитель
по первой строке, получим
.
Физический смысл ротора. Можно
использовать представление о вращении
брошенной в поток маленькой пылинки
(увлекаемой потоком с собой, без его
заметного возмущения) или о вращении
помещённого в поток с закреплённой осью
маленького (без инерции, вращаемого
потоком, заметно не искажая его) колеса
с прямыми (не винтовыми) лопастями. Если
то или другое при взгляде на него
вращается против часовой стрелки, то
это означает, что вектор ротора поля
скорости потока в данной точке имеет
положительную проекцию в направлении
на нас.
3) ряд Дирихле (или обобщённый гармонический ряд)
. (18.3.1)
Если s<1, то
,
и, так как частичные суммы
неограничены, то суммы
и подавно неограничены, т.е. при s<1
ряд (18.3.1) расходится. Пусть теперь s>1.
Как и для гармонического ряда сгруппируем
члены в частичной сумме по степеням
числа 2:
…+
.
Структура каждой скобки:
,
поэтому
(мы воспользовались формулой для
частичной суммы геометрической
прогрессии). Последовательность
ограничена; ряд сходится.
Итак, ряд Дирихле (18.3.1) сходится при
s>1, расходится
при s
1.
Расставьте пределы интегрирования. Перейти к полярным координатам.
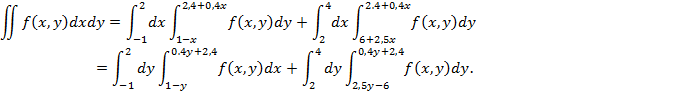
а)
б)
Б
илет
6.
Пусть в пространстве Oxyz задана ограниченная замкнутая область (объём) V, и пусть на области V определена функция
.
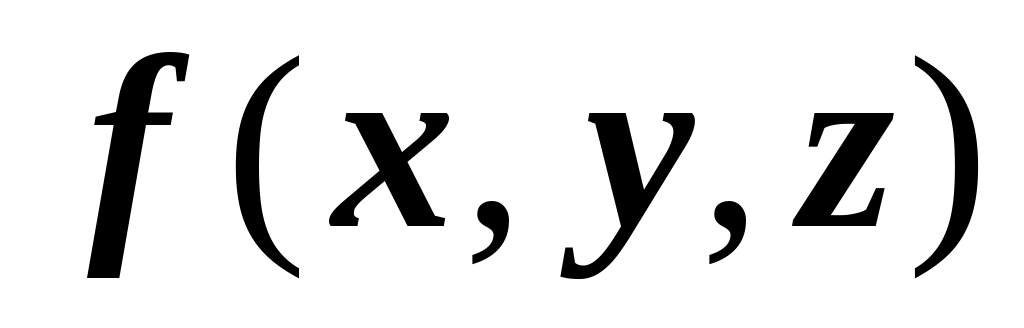Разобьём область V
произвольным образом на
подобластей
(не имеющих общих внутренних точек).
Символом
будем обозначать объём области
;
символом
обозначим наибольший из диаметров
областей
:
.
В каждой из подобластей
выберем произвольную точку
,
вычислим в этой точке значение функции
,
и составим интегральную сумму
.
Если существует предел последовательности
интегральных сумм при
,
не зависящий ни от способа разбиения
области V на
подобласти
,
ни от выбора точек
,
то функция
называется интегрируемой по области
V, а значение этого
предела называется тройным интегралом
от функции
по
области V и
обозначается
.
Если расписать значение
через координаты точки
,
и представить
как
,
получим другое обозначение тройного
интеграла:
.
Итак, кратко,
.
Линейность. Если функции ,
интегрируемы по области V,
то их линейная комбинация
тоже интегрируема по
,
и
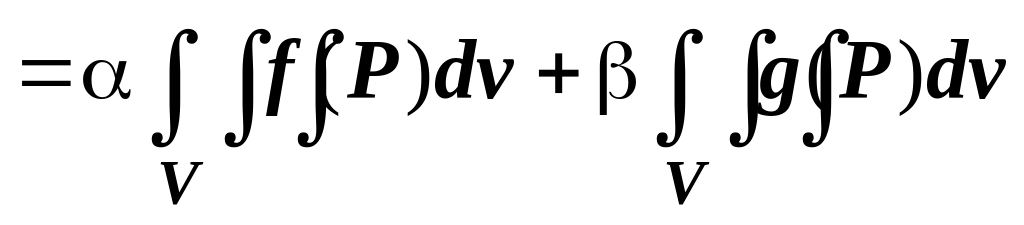.Аддитивность. Если область
является объединением двух областей
и
,
не имеющих общих внутренних точек, то
.Монотонность. Если в любой точке
выполняется неравенство
,
и функции
интегрируемы по области V,
то
.
Теорема Стокса. Пусть в пространственной области V задано гладкое векторное поле
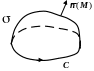(M)
и
- незамкнутая кусочно-гладкая поверхность,
ограниченная контуром С. Единичный
вектор нормали
выбирается так, что с его конца направление
обхода С видно совершающимся
против часовой стрелки. Тогда циркуляция
поля
по контуру С равна потоку ротора
этого поля через поверхность
:
.
Приведённую формулу называют формулой Стокса в векторной форме. В координатной форме формула Стокса имеет вид
или
.
Пример непосредственного вычисления
циркуляции векторного поля и вычисления
по формуле Стокса. Требуется вычислить
циркуляцию поля
по контуру С, образующемуся в
результате пересечения поверхности
с координатными плоскостями.
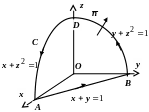Вычисление
по формуле Стокса. Находим ротор поля
:
.
Находим нормаль к
:
,
знак взят с учётом того, что должно быть
.
Теперь
;
спроецируем
на Охz:
;
.
Вычисляем
.
1) Если ряд сходится, то сумма его остатка после n-го члена стремится к нулю при
.Доказательство. Пусть S - сумма исходного ряда (18.2.1),
- сумма его остатка. Из равенства
следует
,
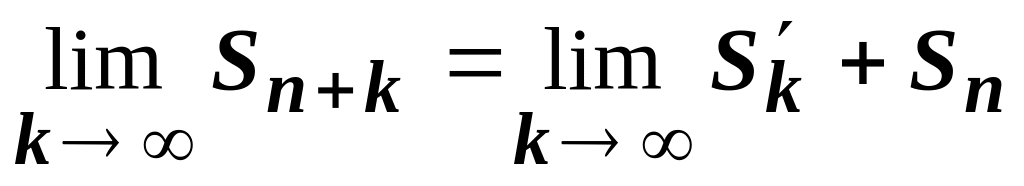т.е.
.
Отсюда
.Здесь тоже можно сделать житейский вывод. Из предыдущего свойства следует, что сходимость ряда определяется сходимостью его остатка, т.е. хвостом ряда, а сумма S ряда, как следует из равенства
,
определяется
пределом
, т.е. началом
ряда.2) Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.
Доказательство. Частичная сумма ряда
есть
;
по свойству предела
.3) Два сходящихся ряда
и
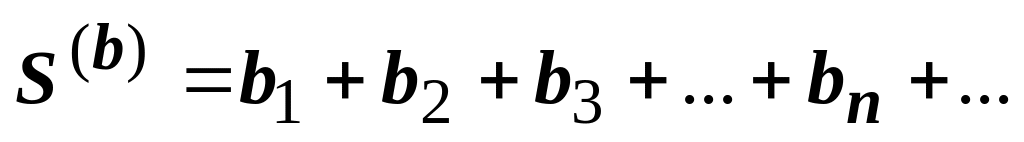можно почленно складывать и вычитать;
ряд
также сходится, и его сумма равна
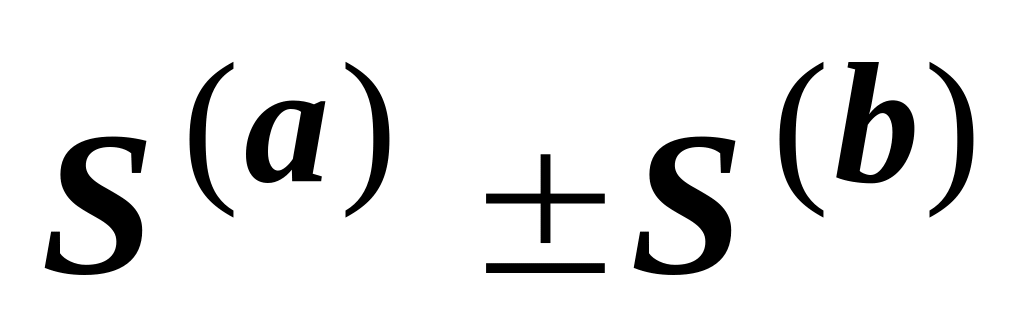.Доказательство и этого свойства - прямое следствие свойств пределов для частичных сумм:
.4)
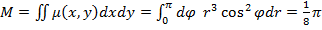
5) П-?
(
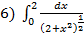
Билет 7.
1.
Определение потенциального поля.
Векторное поле
(M)
называется потенциальным в области V,
если существует такое скалярное поле
,
что
(M)
для
.
Поле
называется потенциалом поля
(M).
Д
окажем,
что если мы фиксируем точку
и возьмём
,
то
,
т.е. определённая таким образом функция
действительно является потенциалом
поля
(M).
Это доказательство полностью повторяет
доказательство теоремы пункта 16.3.3.6.
Вычисление криволинейного интеграла
второго рода в случае, когда выполняются
условия независимости от формы пути.
Именно, требуется доказать, что
.
Действительно, пусть
.
Тогда
,
(на
)
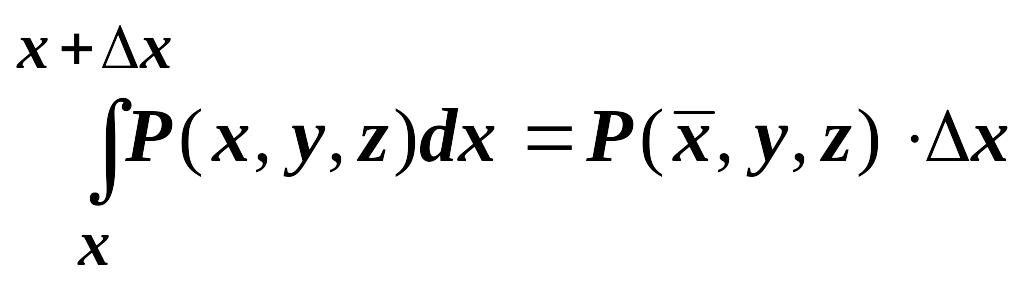(по теореме о среднем)
.
Точка
удовлетворяет условиям
.
Устремим
,
тогда
,
и
.
Аналогично доказывается, что
.
2.
Масса m
материальной кривой
с плотностью (x,y,z)
вычисляется по формуле
.
Пример. Найти массу четверти
лемнискаты
,
если плотность выражается формулой
(x,y)=
.
Решение:
, поэтому
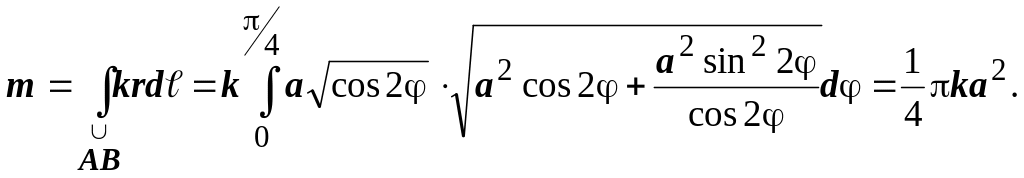
3.
Ряд
сходится равномерно на области G,
если для любого числа
существует такое натуральное число
,
одно и то же для всех точек
,что
при n>N
выполняется неравенство
(или, что тоже самое,
,
где
- остаток ряда после n-го
члена).
Признак Вейерштрасса. Если существует
такой положительный сходящийся числовой
ряд
,
что члены функционального ряда
в любой точке
удовлетворяют неравенству
,
то функциональный ряд сходится равномерно
в области G.
Геометрическая прогрессия
равномерно сходится на любом отрезке
,
целиком лежащем в области сходимости
(-1,1). Действительно, построим мажоранту
для геометрической прогрессии на
.
Из чисел а, b
выберем большее по модулю. Пусть,
например,
.
Тогда для любого
выполняется
.
Таким образом, сходящийся (так как
)
числовой ряд
мажорирует на
функциональный ряд
,
откуда, по признаку Вейерштрасса, следует
равномерная сходимость этого
функционального ряда.
Ряд
равномерно сходится на любой полуоси
,
так как на этом множестве он мажорируется
рядом
.
Ряд
равномерно сходится на всей числовой
оси (мажоранта для этого ряда уже получена
- это ряд
).
4.
Окружность и гипербола.
Находим точки пересечения.
x
=
;
y1=
; y2=
S =
+ 
+ 
;
S =
+ 
+ 
;
В пол. коорд.
r<=2;
r<=1/
Точки пересечения
ϕ= ±arccos(1/4)
S =
+
+ 
5.
Ввиду симметрии кривой, разобьем ее на 4 части
;
;
Замена p=sin t и q=cos t
Ответ m= 4 a^(7/3)
Билет 8.
1.
Определение криволинейного интеграла
первого рода. Пусть в пространстве
переменных x,y,z задана
кусочно-гладкая кривая
,
на которой определена функция
f(x,y,z).
Разобьём кривую точками
на
частей, на каждой из дуг
выберем произвольную точку
,
найдём
и длину
дуги
,
и составим интегральную сумму
.
Если существует предел последовательности
интегральных сумм при
,
не зависящий ни от способа разбиения
кривой на дуги
,
ни от выбора точек
,
то функция f(x,y,z)
называется интегрируемой по кривой
,
а значение этого предела называется
криволинейным интегралом первого рода,
или криволинейным интегралом по длине
дуги от функции f(x,y,z)
по кривой
,
и обозначается
(или
).
Вычисление криволинейного интеграла
первого рода. Примеры. Пусть кривая
задана параметрическими уравнениями
,
где
-
непрерывно дифференцируемые функции,
и пусть точкам
,
которые задают разбиение кривой,
соответствуют значения параметра
,
т.е.
.
Тогда (см. раздел 13.3.
Вычисление длин кривых)
.
По теореме о среднем, существует точка
такая, что
.
Выберем точки
,
получающиеся при этом значении параметра:
.
Тогда интегральная сумма для криволинейного
интеграла
будет равна интегральной сумме для
определенного интеграла
.
Так как
,
то, переходя к пределу при
в равенстве
,
получим
.
2.
Если существует предел последовательности
интегральных сумм при
,
не зависящий ни от способа разбиения
кривой на дуги
,
ни от выбора точек
,
то функция Р(x,y,z)
называется интегрируемой по кривой
,
а значение этого предела называется
криволинейным интегралом второго рода,
или криволинейным интегралом по
координате х от функции Р(x,y,z)
по кривой
,
и обозначается
(или
).
Свойства криволинейного интеграла второго рода. Для этого интеграла существенны следующие свойства:
16.3.3.2.1. Линейность. Если функции
интегрируемы по кривой
(каждая
по своей координате, то по этой кривой
интегрируемы функции
,
и
16.3.3.2.2. Аддитивность. Если кривая
разбита на две части
и
,
не имеющие общих внутренних точек, то
.
16.3.3.2.3. Изменение знака криволинейного
интеграла второго рода при изменении
направления прохождения кривой:
.
4.
r
Точки
пересечения (-4;8) и (2;2)
S = 
S = 
В полярных координатах
Точки пересечения 
S = 
5.
= 
Переходим в обобщенные полярные
координаты y=arcos
z=ar/
rdr = ½ π a^4
6.
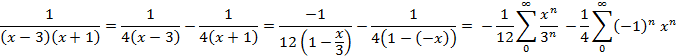
Сходится абсолютно при -1<x<1
Билет 9.
1.
Определение криволинейного интеграла первого рода. Пусть в пространстве переменных x,y,z задана кусочно-гладкая кривая , на которой определена функция f(x,y,z). Разобьём кривую точками на частей, на каждой из дуг выберем произвольную точку , найдём и длину дуги , и составим интегральную сумму . Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения кривой на дуги , ни от выбора точек , то функция f(x,y,z) называется интегрируемой по кривой , а значение этого предела называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги от функции f(x,y,z) по кривой , и обозначается (или ).
Вычисление криволинейного интеграла первого рода. Примеры. Пусть кривая задана параметрическими уравнениями , где - непрерывно дифференцируемые функции, и пусть точкам , которые задают разбиение кривой, соответствуют значения параметра , т.е. . Тогда (см. раздел 13.3. Вычисление длин кривых) . По теореме о среднем, существует точка такая, что . Выберем точки , получающиеся при этом значении параметра: . Тогда интегральная сумма для криволинейного интеграла будет равна интегральной сумме для определенного интеграла . Так как , то, переходя к пределу при в равенстве , получим
.
2.
Свойства потенциального поля.
1. Потенциал определён с точностью до
произвольной постоянной (
).
2. Разность потенциалов в двух точках
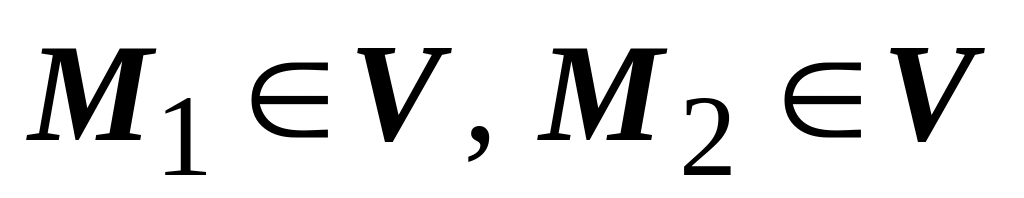определена однозначно.
3. Если поле
(M)
потенциально, то линейный интеграл
этого поля по любой кривой
,
целиком лежащей в V,
определяется только начальной и конечной
точками этой кривой, и не зависит от
формы кривой.
.
Эта формула, как и в плоском случае,
является обобщением формулы Ньютона-Лейбница
для потенциального поля.
4. Циркуляция потенциального в области V поля по любому контуру, лежащему в V, равна нулю.
5. Векторная линия потенциального поля в каждой точке М ортогональна эквипотенциальной поверхности ( т.е. поверхности уровня потенциала), проходящей через точку М.
6. Ротор потенциального векторного поля равен нулю:
.
3.
.
Ряд для этой функции называется биномиальным рядом. Здесь мы будем вычислять производные.
… Ряд Маклорена имеет вид
Ищем интервал сходимости:
, следовательно, интервал сходимости
есть
.
Исследование остаточного члена и
поведение ряда на концах интервала
сходимости проводить не будем; оказывается,
что при
ряд абсолютно сходится в обеих точках
,
при
ряд условно сходится в точке
и расходится в точке
,
при
расходится в обеих точках.
4. (делали на конс)
=
Далее переводим в полярные координаты.
5.
-10/
6.