2.2. Уравнения Максвелла для монохроматических колебаний и уравнения Гельмгольца

Запишем векторы поля Е и Н в комплексном виде

и подставим их в уравнения Максвелла (1.29) для однородного изотропного диэлектрика. После сокращения на множитель эти уравнения примут вид

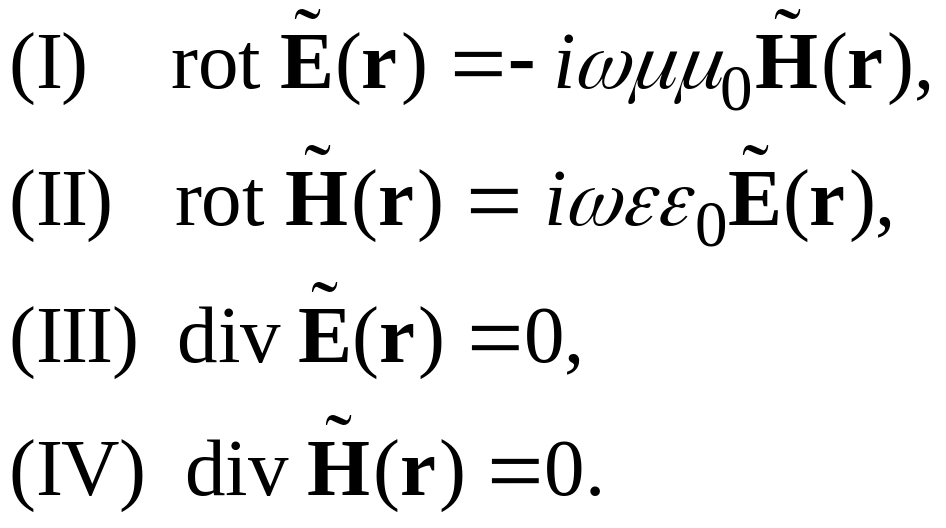
Мы получили уравнения Максвелла для комплексных амплитуд векторов поля и . Напомним, что для изотропных сред параметры ε и μ в уравнениях скалярны, а для анизотропных сред являются тензорами. При отсутствии потерь в среде (т.е. для диэлектрика) материальные параметры ε и μ являются вещественными величинами.

Решая систему , находят комплексные амплитуды векторов поля и .как функции координат. После домножения на получают комплексные выражения векторов поля в виде , а затем выделяют их вещественную часть.

Чтобы получить другой вид уравнений для комплексных амплитуд, подставим поля вида в волновые уравнения (1.30) и (1.31). Для этого вычислим производные:

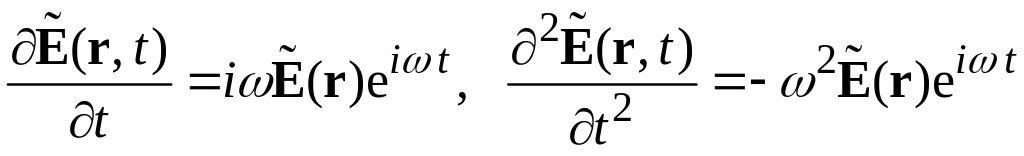
и учтём, что . После сокращения на отличный от нуля множитель волновое уравнение (1.30) для комплексной амплитуды вектора Е принимает вид

где введено обозначение . Ввиду симметрии уравнений Максвелла аналогичное по виду уравнение для комплексной амплитуды вектора магнитного поля H получается из (1.31):

Полученные уравнения носят название уравнений Гельмгольца для комплексных амплитуд монохроматических полей.

2.3. Плоские монохроматические волны

Рассмотрим решение уравнений Гельмгольца , в виде плоской монохроматической волны в простейшем одномерном случае, когда векторы поля зависят от одной координаты ξ, отсчитываемой в направлении распространения волны. В этом случае уравнение записывается как

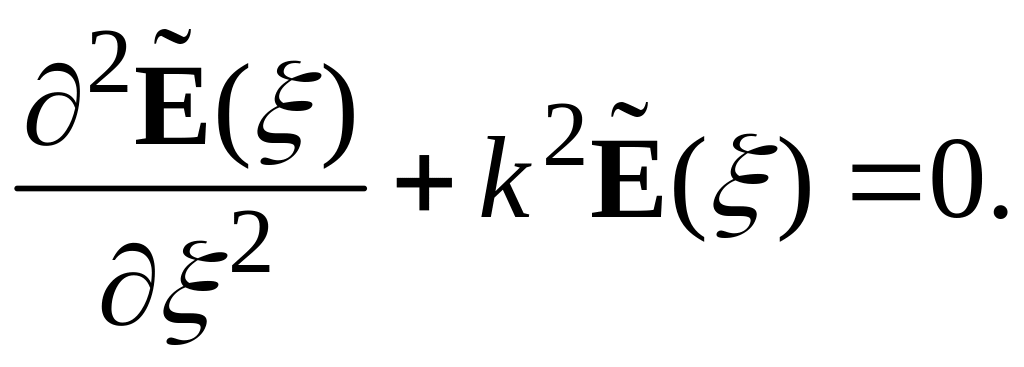
Его общее решение имеет вид:

где и − комплексные постоянные. Подставляя в , получаем

Это решение описывает две встречные бегущие волны, распространяющиеся в положительном и отрицательном направлениях оси ξ.

Поверхности постоянной фазы (волновые поверхности) волны вида представляют собой бесконечные плоскости, перпендикулярные оси ξ. Скорость перемещения в пространстве поверхности постоянной фазы называют фазовой скоростью волны. Для её нахождения запишем условие постоянства фазы и продифференцируем его с учётом того, что для монохроматической волны ω и k − постоянные величины: . Отсюда фазовая скорость

Величину можно записать иначе:

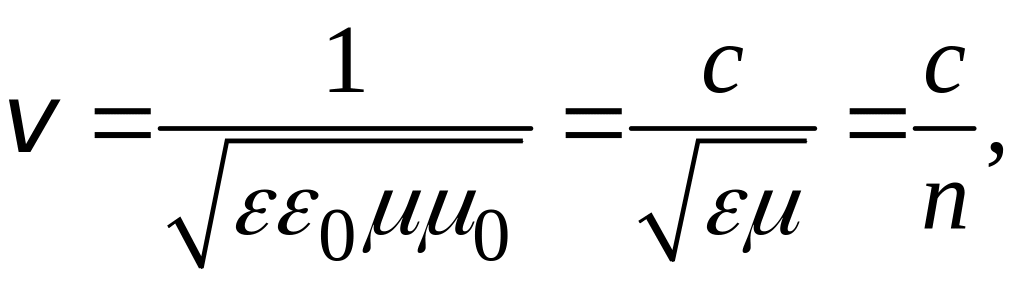
где = 3∙10⁸ м/с – скорость электромагнитной волны в вакууме, а – показатель преломления, определяющий величину фазовой скорости в зависимости от материальных параметров среды и .

Параметр k называют волновым числом:

где n – показатель преломления среды, – волновое число в вакууме. В технической литературе можно встретить другое название параметра k − постоянная распространения волны.

Длина волны λ равна расстоянию, на которое плоскость постоянной фазы распространяется за один период колебаний, т.е. . Волновое число связано с длиной волны соотношением

Длина волны λ в среде в n раз (n – показатель преломления) меньше длины волны в вакууме:

Координату ξ можно представить как ξ = (mr), где m – единичный вектор в направлении оси ξ, r – радиус-вектор произвольной точки пространства (рис. 2.1).

При этом можно ввести волновой вектор k = ±km, сонаправленный с вектором фазовой скорости волны, а по модулю равный волновому числу. Величины ±k в решении тогда имеют смысл проекций волнового вектора на ось ξ. Решению можно придать вид (для волны, распространяющейся в направлении +m):

Аналогичный вид имеет решение уравнения Гельмгольца для вектора магнитного поля:

Соотношения и позволяют определить векторы поля плоской волны в случае произвольной ориентации волнового вектора k относительно координатных осей. Например, в декартовой системе координат

где - проекции вектора k на оси x, y, z соответственно, , – его направляющие косинусы.

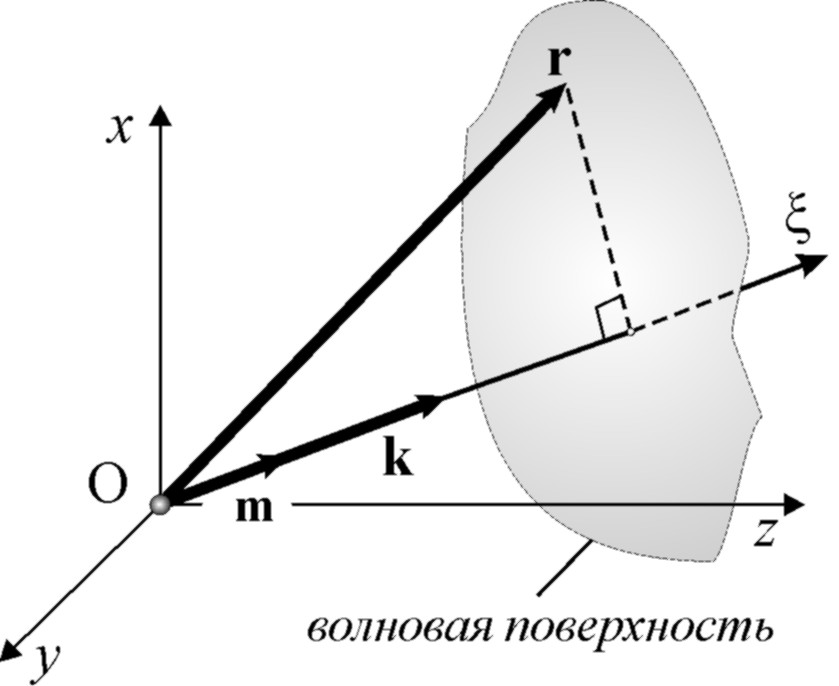
Рис. 2.1.

Для дальнейшего исследования свойств плоских волн подставим решения вида и в уравнения Максвелла . С учётом того, что

уравнения III и IV системы дают

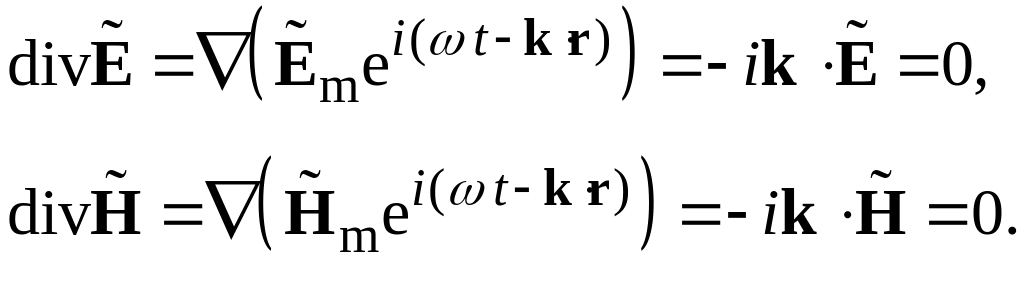
Равенство нулю скалярных произведений в означает, что и , т.е. волна является поперечной как по электрическому, так и по магнитному полю (TEM-волна). Покажем, что к тому же . Подстановка и в левые части уравнений I и II системы приводит к выражениям

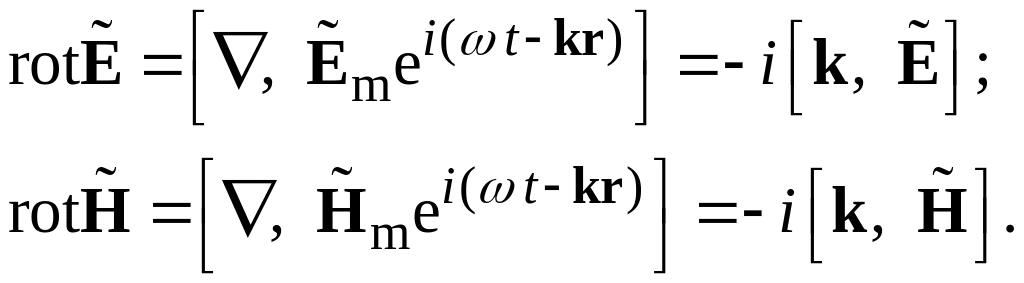
Тогда уравнения I и II приводятся к виду:

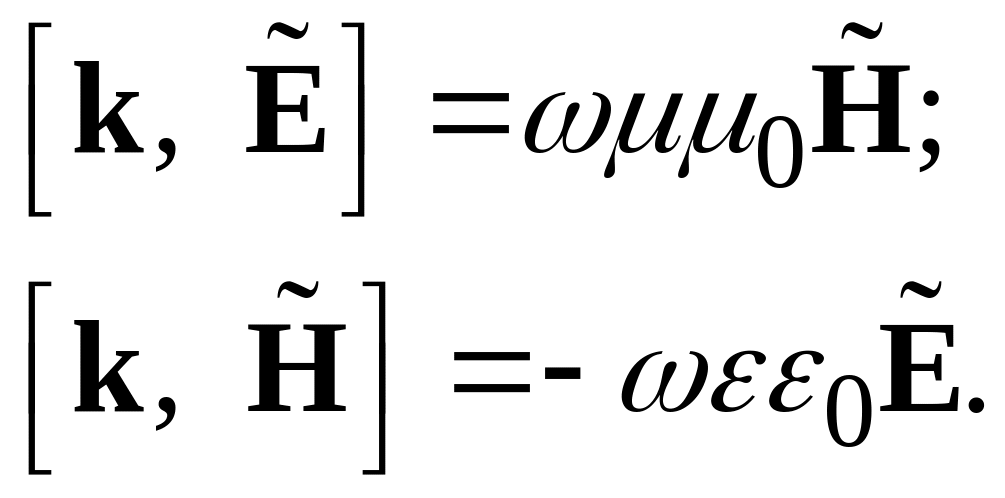
Из уравнений следует, что в случае ПОЛОЖИТЕЛЬНЫХ значений параметров ε и μ три вектора Е, Н и k взаимно перпендикулярны и образуют в указанном порядке ПРАВУЮ тройку векторов (рис. 2.2).

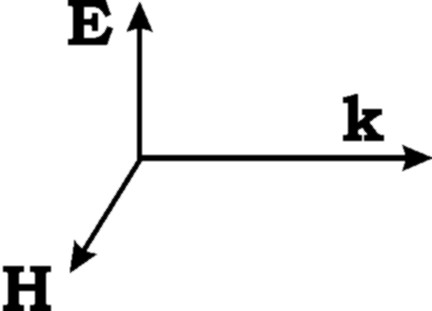
Рис. 2.2.

Возможные случаи отрицательных значений материальных констант будут рассмотрены далее в главе 4.

Из вытекает также связь между модулями векторов Е и Н:

где величина

имеющая размерность сопротивления, называется волновым сопротивлением или импедансом среды. Также из соотношений можно заключить, что колебания векторов Е и Н в плоской волне происходят в одинаковых фазах.