1.5. Волновое уравнение в однородном изотропном диэлектрике

Из уравнений Максвелла вытекает важнейший вывод: переменные электромагнитные поля могут существовать без зарядов и токов. Точнее, поле может существовать, когда породивших его зарядов и токов уже нет. При этом изменение во времени электрического поля приводит к появлению вихревого магнитного поля, а изменение во времени магнитного поля приводит к появлению вихревого электрического поля. Указанные изменения (возмущения) поля переносятся в пространстве в виде электромагнитных волн, которые могут распространяться как в среде, так и в вакууме.

Чтобы убедиться в сказанном, запишем систему уравнений Максвелла для однородного изотропного диэлектрика, т.е среды, в которой отсутствуют свободные заряды и токи проводимости (ρ = 0, j = 0). Используя материальные уравнения и , в ней можно уменьшить число неизвестных, исключив, например, векторы D и B:

Величины E и Н, являющиеся переменными системы уравнений , в теории электромагнитных волн принято называть векторами поля. Вектор Е называют вектором электрического поля или, для краткости, «электрическим полем», соответственно, вектор Н – вектором магнитного поля или «магнитным полем».

Дифференцируя уравнение II системы по времени и заменяя в полученном уравнении из уравнения II, приходим к уравнению:

Пользуясь формулой векторного анализа и учитывая уравнение III, получаем:

где − дифференциальный оператор Лапласа, а – постоянная величина, имеющая размерность скорости. Уравнение называется однородным волновым уравнением для вектора Е. Ввиду симметрии уравнений относительно векторов поля, такому же уравнению удовлетворяет и вектор магнитного поля Н:

Простейшим решением данных волновых уравнений является решение в виде плоской волны, распространяющейся в некотором фиксированном направлении, заданном единичным вектором m. В этом случае векторы Е и Н зависят лишь от одной пространственной координаты ξ = (mr), отсчитываемой по направлению единичного вектора m (рис. 1.1).

Рис. 1.1.

В этом случае и уравнения вида , преобразуются в одномерное волновое уравнение:

где u − любая из декартовых компонент векторов E, Н.

Общее решение уравнения записывается как

где − произвольные дважды дифференцируемые функции. Поверхность, в каждой точке которой в любой момент времени векторы поля имеют одинаковые значения, называется волновой поверхностью. Для волны вида волновой поверхностью является любая плоскость, перпендикулярная направлению m. Поэтому волна данного типа и получила название «плоской».

Для уяснения физического смысла решения рассмотрим вначале решение . Пусть в некоторый момент времени t = 0 в некоторой плоскости ξ = const функция имеет значение . Спустя промежуток времени t функция будет иметь такое же значение на расстоянии + от первоначального места. Значит, с течением времени график этой функции будет смещаться со скоростью v в направлении +m, но форма графика при этом будет оставаться неизменной (см. рис. 1.2). Аналогично, график функции смещается с течением времени со скоростью v в направлении –m. Таким образом, решение является суперпозицией двух возмущений поля (т.е. двух волн), распространяющихся в противоположных направлениях вдоль оси ξ. Константа v при этом имеет смысл скорости распространения волны.

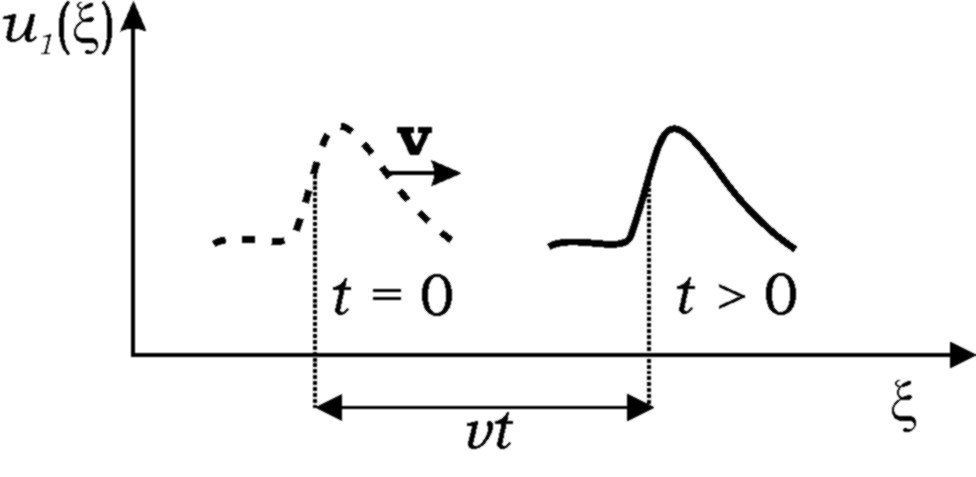
Рис.1.2.

Теперь рассмотрим решение волновых уравнений в виде сферической волны. Сферическая волна возбуждается точечным источником в неограниченном однородном и изотропном пространстве, а векторы поля зависят лишь от радиальной координаты r сферической системы координат.

Используя выражение для радиальной части оператора Лапласа в сферических координатах

однородное волновое уравнение для скалярной функции u можно привести к виду

аналогичному уравнению . Его общим решением являются произвольные функции аргумента , поэтому выражение для компонент векторов поля сферической волны имеет вид

Первое слагаемое в описывает волну, распространяющуюся от начала координат в радиальном направлении со скоростью v (расходящаяся волна). Второму слагаемому соответствует волна, сходящаяся к началу координат. В произвольный момент времени значения функции одинаковы на сфере любого фиксированного радиуса r, т.е. волновые поверхности сферической волны имеют вид концентрических сфер. Согласно , амплитуда сферических волн убывает обратно пропорционально расстоянию r от начала координат.