6.8. Продольно намагниченный феррит. Эффект Фарадея

Рассмотрим теперь задачу о распространении плоской монохроматической волны в неограниченном феррите при условии, что оно происходит в направлении вектора напряжённости магнитного поля , намагничивающего феррит до насыщения. Запишем уравнения в проекциях на оси x и y декартовой системы координат. Учтём, что магнитная проницаемость феррита является тензором вида , а также то, что для плоской волны производные векторов поля по координатам x и y равны нулю:

Проекции на ось z дают , т.е. волна является поперечной в отношении как электрического, так и магнитного поля.

Перейдём в системе к новым переменным , которые называются циркулярными:

Для этого второе и четвёртое уравнения системы сложим с первым и третьим, умноженными на i или на –i. В результате получим две независимых подсистемы из двух уравнений каждая: первая – для переменных вторая – для :

Решения этих подсистем соответствуют двум собственным (нормальным) волнам продольно намагниченного феррита:

где − волновое число для вакуума. Эти волны являются поперечными волнами круговой поляризации, имеющими различное направление вращения. Волна с полями является волной с ПРАВЫМ направлением вращения (рис.6.9а): если смотреть НАВСТРЕЧУ вектору , то конец вектора поля или описывает окружность, вращаясь ПРОТИВ ЧАСОВОЙ СТРЕЛКИ. Соответственно, волна с полями - волна с ЛЕВЫМ направлением вращения (конец вектора поля описывает окружность, двигаясь ПО ЧАСОВОЙ СТРЕЛКЕ, рис.6.9б).

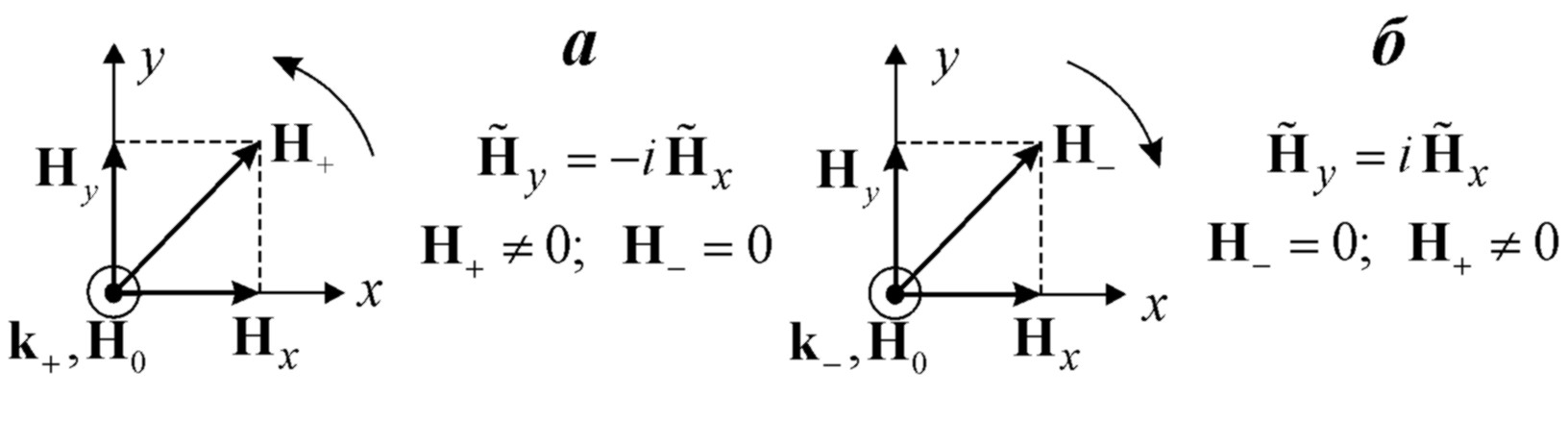
Рис. 6.9.

Чтобы убедиться в сказанном, вспомним, что для волны с круговой поляризацией взаимно ортогональные составляющие векторов поля (например, магнитного) должны иметь одинаковые амплитуды и фазовый сдвиг . Значит, они должны быть связаны соотношениями , где верхний знак соответствует правому, а нижний − левому направлению вращения. Для волны ПРАВОЙ поляризации (сдвиг фаз ) имеем:

а для второй волны с ЛЕВОЙ поляризацией (сдвиг фаз ):

Рис. 6.10.

Нормальные волны продольно намагниченного феррита имеют различные волновые характеристики и , что связано с различием их эффективных магнитных проницаемостей и . При этом зависимости от частоты ω и внешнего поля имеют резонансный характер: в отсутствие потерь при или . Таким образом, для волны с правой круговой поляризацией может наблюдаться ферромагнитный резонанс. Напротив, аналогичные зависимости являются монотонными, т.е. ферромагнитный резонанс для волны с левой поляризацией отсутствует (см. рис. 6.10).

Собственные волны с правой и левой круговой поляризацией распространяются в феррите с различными фазовыми скоростями и . Это приводит к поляризационному эффекту Фарадея: вращению плоскости поляризации линейно поляризованной волны в продольно намагниченном феррите.

Пусть на слой продольно намагниченного феррита из вакуума падает нормально волна, магнитное поле которой линейно поляризовано, например, вдоль оси x (см. рис. 6.11). Волну с линейной поляризацией можно представить в виде суперпозиции двух волн с круговой поляризацией, имеющих одинаковые амплитуды и противоположные направления вращения:

Вводя обозначения , , можно переписать как

Угол ψ, который образует плоскость поляризации волны с осью x, найдётся из :

Из видно, что плоскость поляризации волны по мере её распространения в феррите поворачивается. Если смотреть навстречу направлению внешнего магнитного поля, то поворот происходит против часовой стрелки. Если волна распространяется навстречу направлению , то направление вращения плоскости поляризации изменяется на противоположное. Таким образом, если волна проходит в феррите одинаковое расстояние сначала по направлению , а затем обратно, то её плоскость поляризации не возвращается в исходное положение, а оказывается повёрнутой на угол 2 .

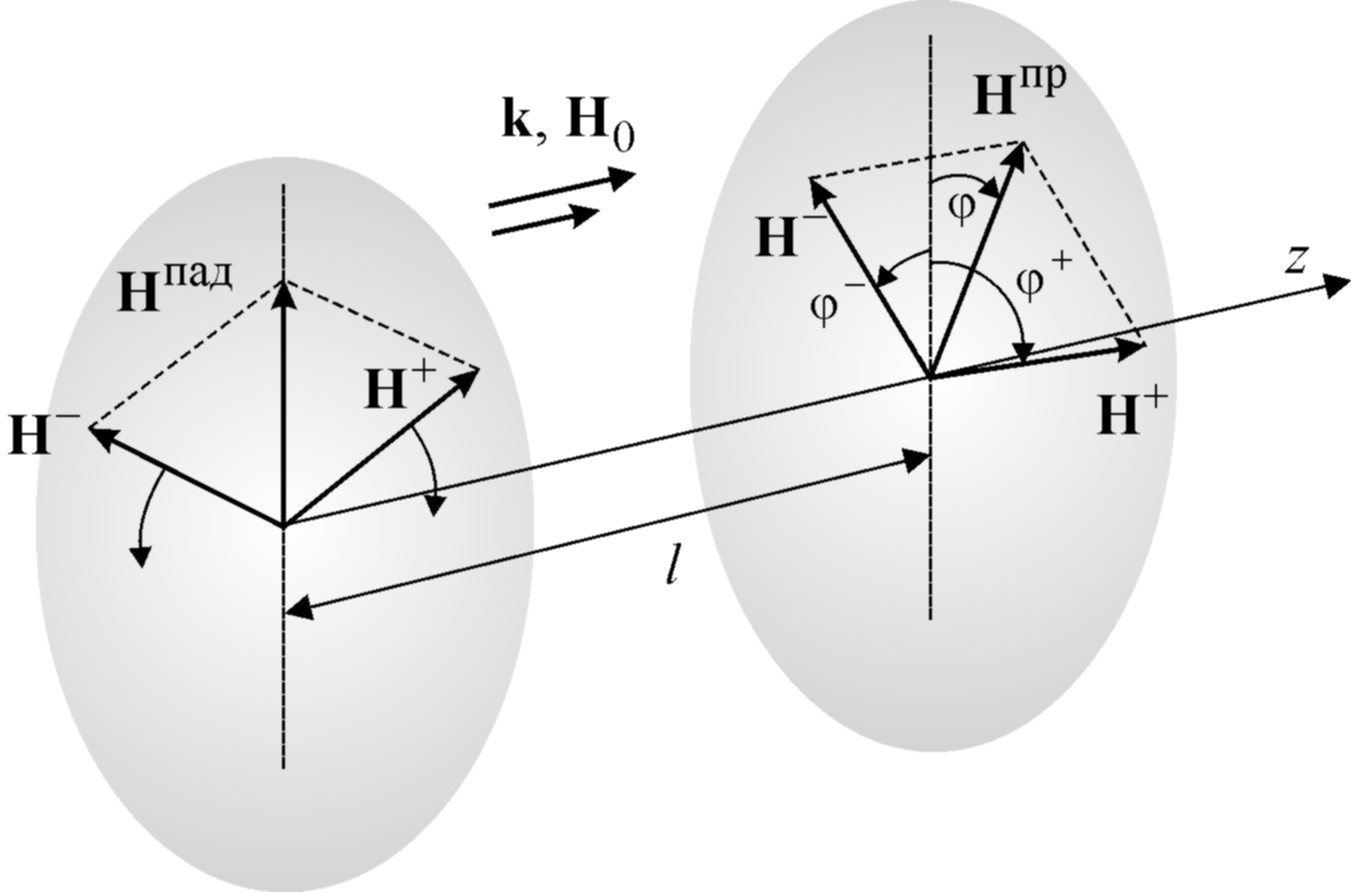
Рис. 6.11.

Величину

определяющую величину эффекта Фарадея, называют постоянной вращения или постоянной Фарадея.

Заметим, что электрическое поле волны, прошедшей через феррит, окажется поляризованным эллиптически ввиду различия импедансов и двух нормальных волн. На практике магнитное поле прошедшей волны также приобретает некоторую эллиптичность из-за наличия потерь в реальном феррите.