6.7. Поперечно намагниченный феррит. Эффект Коттона – Мутона

Рассмотрим плоскую монохроматическую волну, распространяющуюся в феррите ПЕРПЕНДИКУЛЯРНО направлению внешнего намагничивающего поля (например, в направлении оси y. Феррит характеризуется скалярной диэлектрической проницаемостью ε и тензором магнитной проницаемости вида .

Запишем уравнения Максвелла для комплексных амплитуд векторов поля ,

и спроектируем их на оси выбранной системы координат. В левой части получившихся выражений учтём, что волна плоская и частные производные по координатам x и z равны нулю. При записи проекций первого уравнения системы необходимо учесть тензорный характер магнитной проницаемости. В результате получается система шести скалярных уравнений, которая разбивается на две независимых подсистемы. Первая подсистема содержит компоненты полей :

Во вторую подсистему входят остальные компоненты :

Подсистемы и соответствуют двум независимым собственным (нормальным) волнам поперечно намагниченного феррита.

Решением первой подсистемы является так называемая «необыкновенная» волна. Она имеет только одну (поперечную) компоненту электрического поля , параллельную подмагничивающему полю и две компоненты магнитного поля: поперечную и продольную . Компоненты магнитного поля связаны соотношением

которое вытекает из второго уравнения подсистемы . Таким образом, первая нормальная волна является поперечной и линейно поляризованной только в отношении электрического поля. Магнитное поле данной волны эллиптически поляризовано в плоскости (x, y). Это видно из формулы : множитель i указывает, что сдвиг фаз колебаний компонент и равен π/2, а их амплитуды отличаются в раз. Отметим, что появление продольной составляющей магнитного поля напрямую связано с гиротропией феррита: согласно при  = 0  = 0.

Исключая из подсистемы , приводим её к виду

где введено обозначение . Система по виду совпадает с аналогичной системой (2.22) для изотропного диэлектрика с тем отличием, что роль магнитной проницаемости играет величина (её иногда называют «поперечной магнитной проницаемостью»). По аналогии с решением системы (2.22) (см. выражения (2.24), (2.25)), решение системы может быть записано в виде плоской монохроматической волны, для которой волновое число и импеданс определяются как

Так же, как и компоненты тензора высокочастотной магнитной проницаемости , поперечная магнитная проницаемость обладает сильной дисперсией: для неё характерна резонансная зависимость от частоты ω и напряжённости внешнего поля .

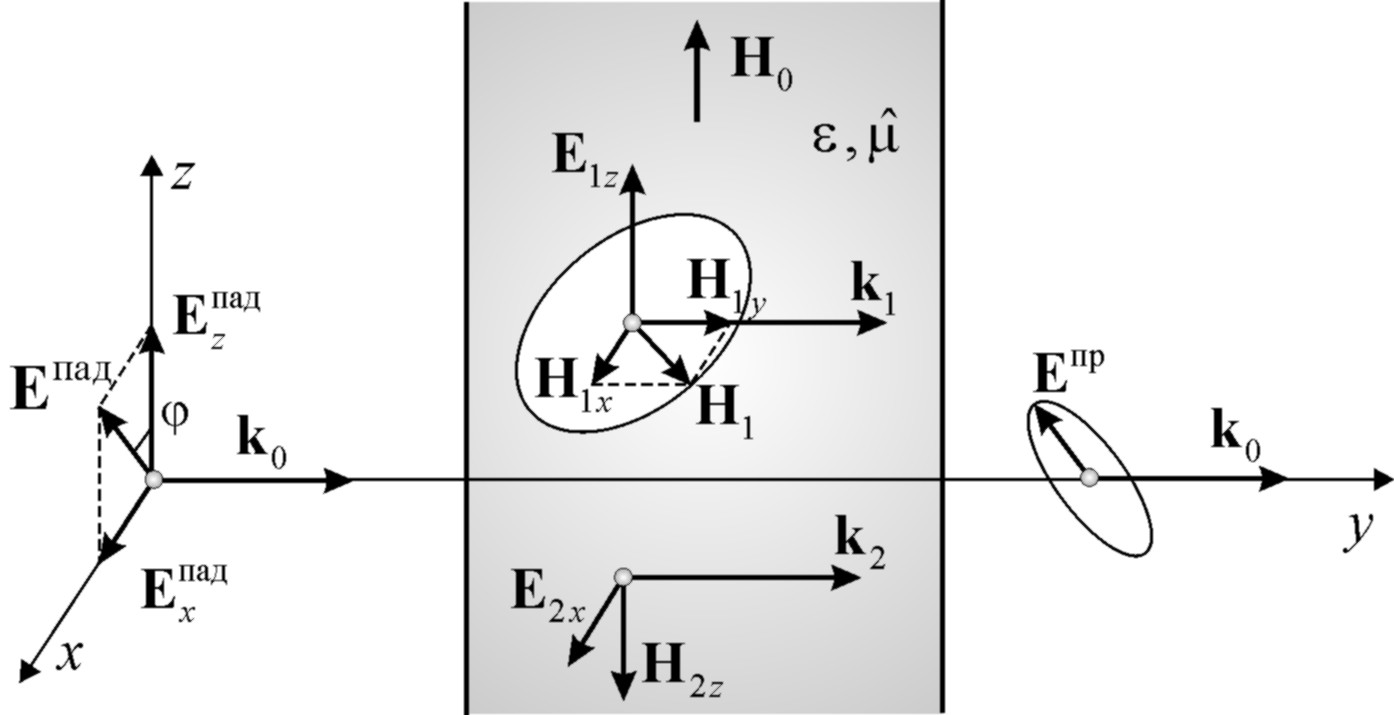
Рис. 6.8.

Решением подсистемы является вторая («обыкновенная») нормальная волна. Она не имеет особенностей по сравнению с «обычным», изотропным диэлектриком. Её поля линейно поляризованы и имеют только поперечные составляющие и , а  = 0. Волновые характеристики «обыкновенной» волны и , в отличие от и , не обладают частотной и полевой дисперсией:

Рассмотрим нормальное падение линейно поляризованной волны на плоский слой поперечно намагниченного феррита (рис. 6.8).

Если электрическое поле падающей волны поляризовано под углом φ к полю , отличным от 0 и π/2, то в слое феррита возбуждаются две нормальные волны. Составляющая электрического поля , параллельная полю , возбуждает «необыкновенную» волну, а ортогональная полю составляющая − «обыкновенную». Эти волны распространяются в феррите с различными фазовыми скоростями и . В результате на выходе из феррита эти волны приобретут сдвиг по фазе и при сложении дадут волну эллиптической поляризации. Параметры эллипса поляризации будут зависеть от толщины ферритового слоя, угла φ, внешнего магнитного поля и частоты ω. Описанный эффект преобразования поляризации волны слоем поперечно намагниченного феррита называется эффектом Коттóна – Мутóна.

Эффект Коттона – Мутона, а также резонансные свойства «необыкновенной» волны в поперечно намагниченном феррите находят применение в технике СВЧ для создания устройств, управляемых внешним магнитным полем, например, вентилей, поляризаторов и модуляторов.