6.3. Тензор диэлектрической проницаемости магнитоактивной плазмы

Анизотропные среды, у которых диэлектрическая или магнитная проницаемость описывается несимметричным тензором, называются гиротропными. Среда, которая приобретает гиротропные свойства под действием постоянного внешнего магнитного поля, называется магнитоактивной. Примерами таких сред являются намагниченная плазма и намагниченный феррит. Магнитоактивная плазма служит примером гироэлектрической среды, у которой несимметричным тензором является диэлектрическая проницаемость, тогда как μ – скаляр. У намагниченного феррита несимметричным тензором является магнитная проницаемость. В этом случае среду называют гиромагнитной.

Плазма − это ионизованный газ, представляющий собой смесь нейтральных и заряженных частиц. Обычно заряженные частицы – это положительно заряженные ионы и отрицательно заряженные свободные электроны. В целом плазма является электрически нейтральной. В дальнейшем при рассмотрении движения частиц плазмы во внешних полях будем пренебрегать движением ионов. Также не будем учитывать столкновения заряженных частиц друг с другом, т.е. пренебрежём проводимостью плазмы. При этом в уравнении Максвелла II системы (1.1) можно пренебречь током проводимости по сравнению с током смещения.

Вначале рассмотрим ненамагниченную плазму. Ввиду хаотичности теплового движения частиц такая плазма должна быть изотропной. Пусть плазма находится в переменном электрическом поле вида

Уравнение движения свободного электрона запишется как

где m – масса электрона, e – элементарный заряд, r – смещение электрона под действием поля. Уравнение легко интегрируется, что с учётом даёт

Смещение электрона r от первоначального положения приводит к появлению электрического дипольного момента . Если в единице объёма содержится N свободных электронов, получающих под действием поля одинаковое смещение, то суммарный дипольный момент единицы объёма (вектор поляризации) с учётом равен

Используя выражения (1.11) и (1.12) вектора электрической индукции D, для диэлектрической проницаемости ε плазмы получаем

где введена плазменная частота :

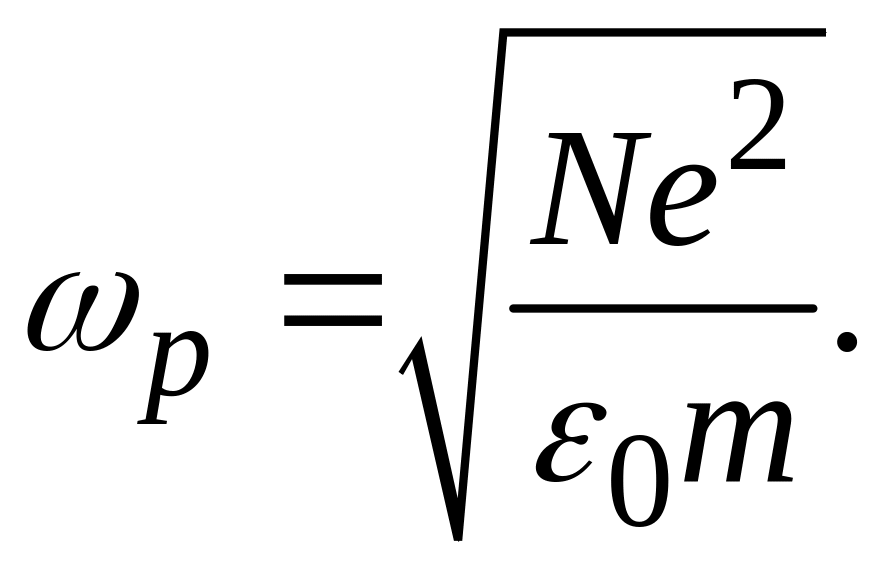
Диэлектрическая проницаемость – скалярная величина, т.е. ненамагниченная плазма в самом деле является изотропной средой. Как видно из , ε обладает частотной дисперсией. Плазменная частота играет роль частоты «отсечки», ниже которой электромагнитная волна в изотропной плазме распространяться не может: при и показатель преломления плазмы становится мнимой величиной.

Пусть теперь наряду с полем на плазму воздействует постоянное внешнее магнитное поле, приложенное вдоль оси z: . Таким образом, в плазме появляется физически выделенное направление. Под действием магнитной составляющей силы Лоренца (1.2) свободные электроны плазмы движутся по винтовым траекториям, вращаясь вокруг направления внешнего поля с циклической частотой

не зависящей ни от скорости частицы, ни от радиуса орбиты. Частоту называют циклотронной или резонансной частотой электрона. При наличии переменного электрического поля вида траектории электронов будут иметь более сложный характер, причём их вид будет зависеть от угла, который образует вектор Е с вектором . Таким образом, вектор поляризации P плазмы будет зависеть от направления и намагниченная плазма будет проявлять свойства анизотропной среды.

Поле Е может являться переменным электрическим полем распространяющейся в плазме электромагнитной волны. Для того чтобы были правомерны оговоренные выше приближения, частота волны ω должна удовлетворять следующим условиям. Ионы плазмы можно считать неподвижными, если , где − циклотронная частота иона. Если, кроме того, , где ν – частота соударений электронов с ионами и нейтральными частицами, то можно пренебречь токами проводимости по сравнению с токами смещения (фактически – пренебречь потерями в плазме). Определим диэлектрическую проницаемость магнитоактивной плазмы, удовлетворяющей данным условиям.

Ввиду гармонической зависимости поля Е от времени, такой же зависимостью будет обладать и вектор поляризации Р. Поэтому

(v – скорость электрона), откуда

Скорость v будем искать с помощью уравнения движения электрона под действием силы Лоренца (1.2):

Временная зависимость скорости v должна быть гармонической, т.е. . С учётом этого спроектируем векторное уравнение на оси декартовой системы координат:

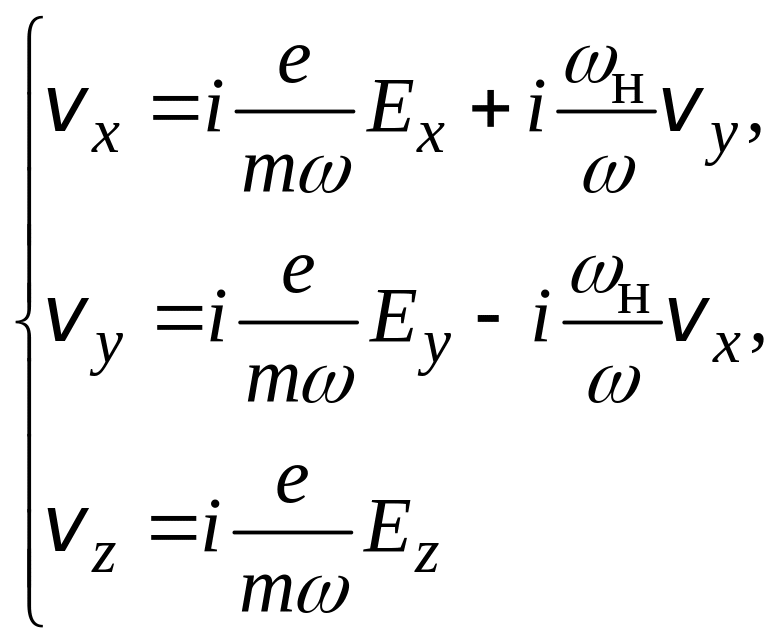
(где введена циклотронная частота ). Решая систему относительно проекций скорости и подставляя полученные выражения в , приходим к следующим выражениям проекций вектора электрической индукции D:

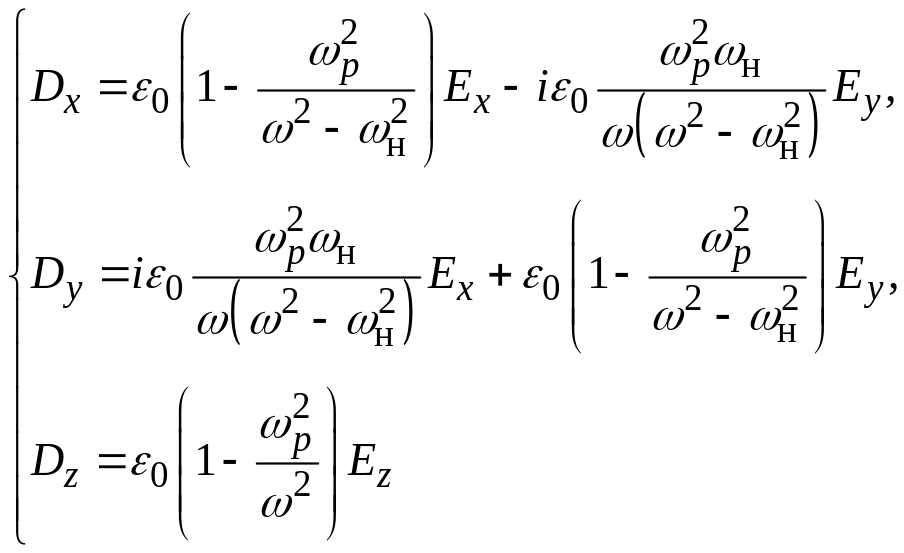
(при выводе использовано определение плазменной частоты ). Из следует, что диэлектрическая проницаемость магнитоактивной плазмы является тензором вида

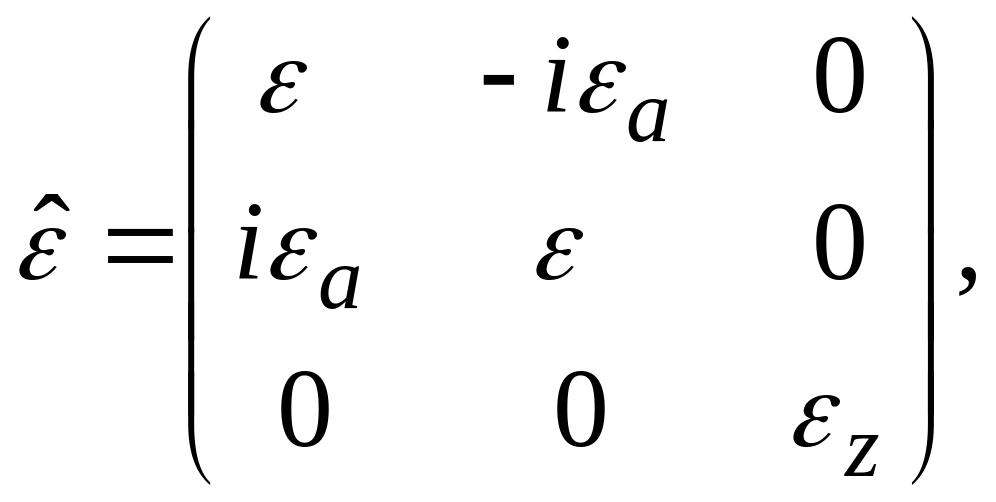
где .

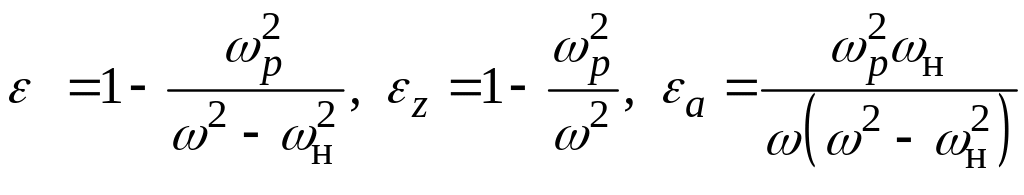Из видно, что в магнитоактивной плазме существует резонанс: при некоторые компоненты тензора стремятся к бесконечности. Наличие расходимостей связано с тем, что при выводе не учитывались диссипативные процессы, т.е. проводимость плазмы.