4.5. Среды с отрицательным значением диэлектрической или магнитной проницаемости. Электромагнитное туннелирование

Рассмотрим особенности распространения электромагнитных волн в среде с отрицательным значением одной из материальных констант. Рассмотрим идеальный случай отсутствия потерь ( ). Для определённости будем считать, что при (т.е. в формулах , , ). Расчёт по формуле дает чисто мнимый показатель преломления

а, значит, и чисто мнимое волновое число

где − волновое число в вакууме. Чисто мнимым, согласно , будет и импеданс среды:

С учётом и выражения для компонент электрического и магнитного полей волны, распространяющейся в направлении оси z, примут вид:

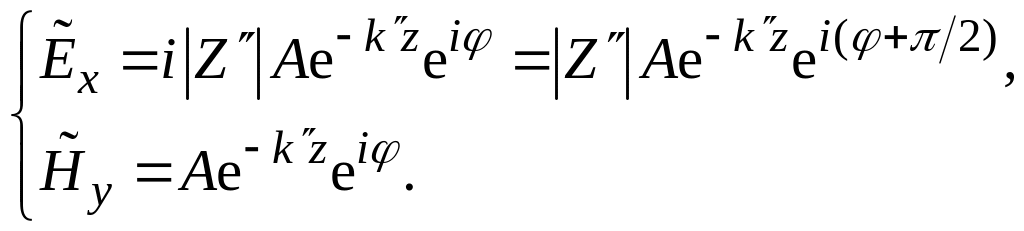
где . Выделим вещественную часть комплексных выражений :

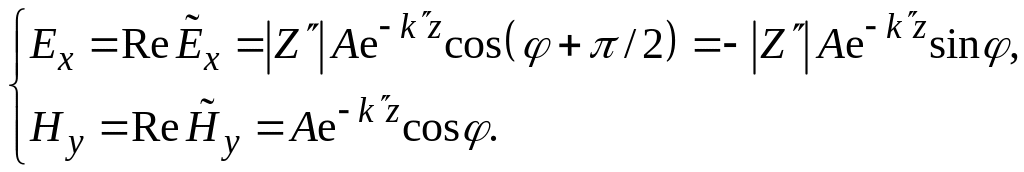
Анализируя , приходим к следующим выводам.

1. Ввиду того, что , данный процесс нельзя назвать бегущей волной. Это – гармоническое электромагнитное колебание с амплитудой, экспоненциально спадающей в направлении оси z.

2. Сдвиг фаз между колебаниями векторов Е и Н составляет π/2, т.е. и являются реактивными компонентами полей. Значит, средний поток энергии (интенсивность) в направлении оси z должен быть равен нулю. Это подтверждает прямой расчёт:

т.е. поток энергии колеблется с частотой 2ω, а его среднее значение за период равно нулю.

3. Плотность электрической и магнитной энергии имеет вид:

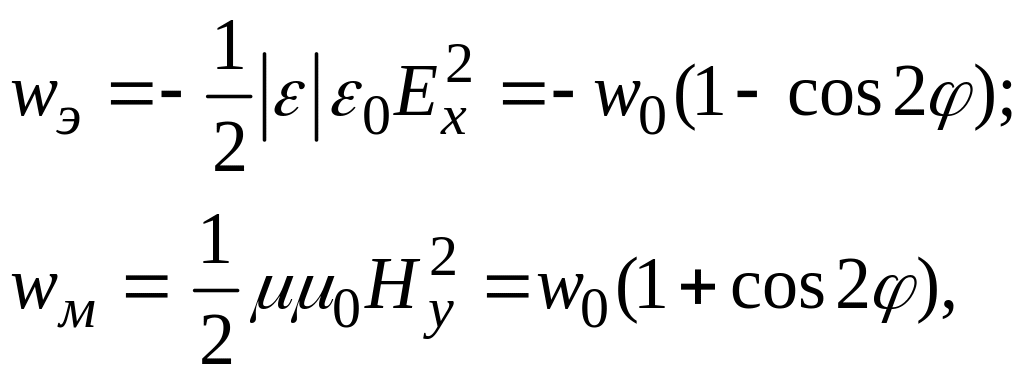
где . Величины и колеблются с частотой 2ω около средних значений . При этом наблюдается периодический процесс взаимного превращения энергии электрического и магнитного полей, который полностью аналогичен энергетическим процессам, протекающим в идеальном колебательном контуре, обладающим чисто реактивным сопротивлением. Суммарная плотность энергии колеблется около среднего значения . С точки зрения энергетических соотношений данный процесс напоминает стоячую электромагнитную волну (см. п. 2.7) с тем отличием, что в стоячей волне .

Описанный здесь процесс можно реализовать вблизи плоской границы раздела двух сред: вакуума (воздуха) 1 с и среды 2 с . Пусть из среды 1 на границу раздела z = 0 нормально падает плоская монохроматическая волна. Её электромагнитное поле проникает во вторую среду, где устанавливается затухающее в направлении оси z колебание вида , обладающее колеблющейся электромагнитной энергией . Также присутствует и мгновенный поток энергии , благодаря которому в течение половины периода колебаний энергия поступает внутрь среды 2, а затем в течение такого же времени выходит обратно. Средний поток через границу раздела равен нулю; это означает, что происходит полное отражение падающей волны (даже при нормальном падении!) и перед границей образуется стоячая волна. Распределение амплитуды электрического поля вдоль оси z для этого случая представлено на рис. 4.5а.

Однако полное отражение «нарушается», если волна отражается от достаточно тонкого слоя среды 2 (толщиной порядка ). При этом на «задней» поверхности слоя формируется ещё одно колебание, затухающее в направлении, противоположном z. Из трёх составляющих суммарного потока энергии встречных волн (формула ) в данном случае ( ) будет отличен от нуля интерференционный поток энергии. При он не зависит от координаты z:

где − модули, а и − фазовые углы амплитудных коэффициентов двух встречных волн внутри слоя (все эти величины могут быть найдены из граничных условий). Благодаря наличию интерференционного потока электромагнитная энергия частично «просачивается» или, как говорят, «туннелирует» через слой среды, в которой одиночная волна не переносит энергии. В этом случае говорят, что имеет место «нарушенное полное отражение» или «электромагнитное туннелирование» (см. рис. 4.5б). В диэлектрике за слоем (среда 3) распространяется бегущая волна (с увеличением толщины слоя среды 2 её амплитуда асимптотически приближается к нулю). Волна перед слоем уже не будет чисто стоячей (амплитуда поля в ее «узлах» отлична от нуля).

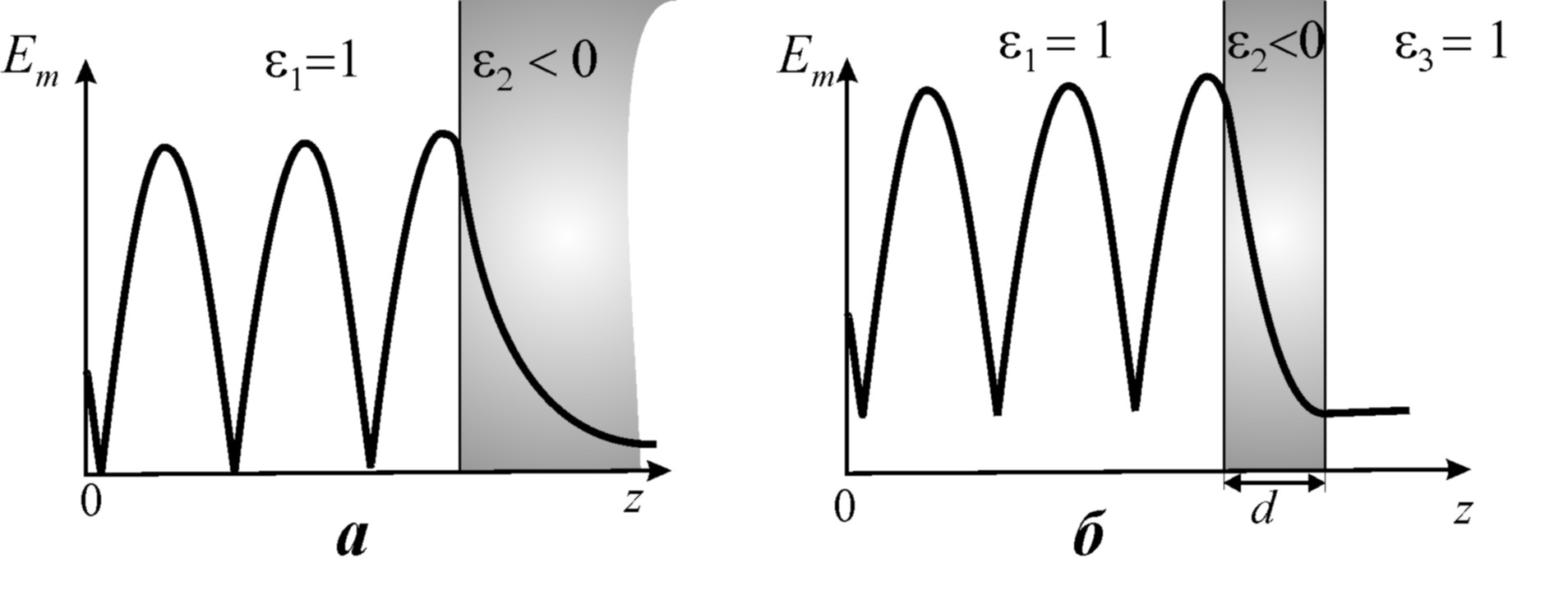
Рис. 4.5.

В реальном случае среда обладает потерями ( ) и вещественные части постоянной распространения и импеданса отличны от нуля. Волна в среде 2 будет тогда распространяющейся, переносящей энергию волной, что приведёт к нарушению полного отражения даже в ситуации, изображённой на рис. 4.5а. Однако ввиду соотношения эта волна будет сильно затухающей.

Следует заметить, что свойства сред с отрицательной проницаемостью или были здесь рассмотрены в идеализированном случае бездисперсной среды. Все реально существующие (природные и искусственные) среды с отрицательной проницаемостью обладают частотной дисперсией. В определённых диапазонах частот отрицательную проницаемость или обнаруживают диэлектрики в области линий резонансного поглощения, металлы в видимой области спектра, намагниченные ферриты и плазма, а также многие искусственные композитные материалы. Более строгое рассмотрение с учётом дисперсии требует корректировки некоторых соотношений, в частности, формул для плотности электромагнитной энергии.