4.4. Среды с одновременно отрицательными значениями диэлектрической и магнитной проницаемостей. Отрицательное преломление

Необычные электродинамические свойства сред с отрицательными материальными параметрами ( ) были подробно рассмотрены в теоретических работах В.Г. Веселаго 1960-х гг., где впервые было введено понятие отрицательного показателя преломления. Первые сообщения о создании искусственных материалов с такими свойствами появились в начале 2000-х гг. Эти материалы представляют собой композиты, состоящие из множества металлических элементов, вкрапленных в диэлектрическую основу. Элементы располагаются в строгом порядке и образуют структуру, похожую на решётку кристалла. В решётке чередуются элементы двух типов. Первый тип – тонкие металлические стерженьки, представляющие собой антенны, взаимодействующие с электрическим полем распространяющейся в структуре волны. Второй тип − колечки с прорезями, взаимодействующие с магнитной компонентой поля. Если размеры элементов и расстояние между ними существенно меньше длины волны падающего излучения, то данную структуру можно рассматривать как сплошную среду, являющуюся однородной и изотропной.

Обратимся к формулам (2.20), связывающим векторы Е, Н и k плоской монохроматической волны. Рассмотрим однородную изотропную не поглощающую среду с отрицательными материальными константами  < 0 и  < 0. Тогда , скалярны и вещественны: и соотношения (2.20) при этом можно переписать как

Сравнивая (2.20) с , легко видеть, что одновременная смена знаков и переводит правую тройку векторов k, Е, Н в левую (см. рис. 4.2). Значит, среда с должна быть левой с отрицательным показателем преломления, а волна в такой среде является обратной.

Для того, чтобы доказать отрицательность показателя преломления, отрицательные проницаемости, даже в случае пренебрежения потерями, следует рассмотреть как комплексные величины вида , и использовать результаты п. 4.3 (см. частный случай 2). Полагая , получаем, что и , , т.е.

Отрицательность показателя преломления проявляется в необычной реализации некоторых законов оптики, прежде всего, закона Снеллиуса. Рассмотрим отражение и преломление плоской монохроматической волны на границе раздела среды 1 с и левой среды 2 с . Если формально записать закон Снеллиуса (3.7) с учётом отрицательного знака , то окажется, что

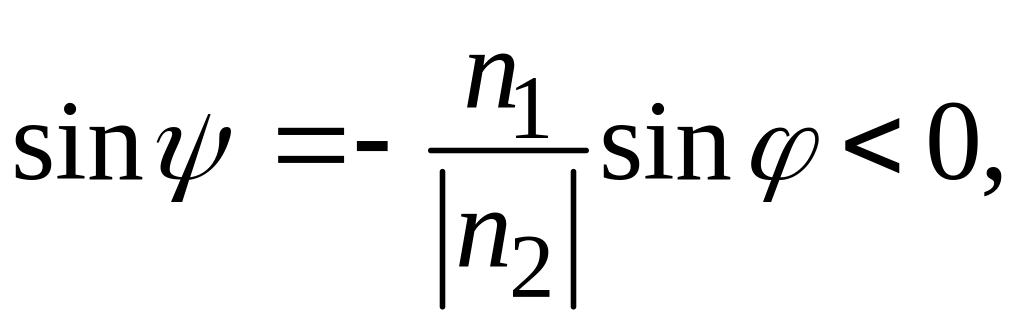
т.е. угол преломления ψ будет отрицательным. Это означает, что в отличие от «обычного» случая отражения и преломления на границе двух «правых» сред (рис. 4.4а), падающий и преломлённый лучи лежат по одну сторону от нормали, восстановленной в точке падения (рис. 4.4б).

Вектор Пойнтинга преломлённой волны в левой среде по-прежнему направлен вглубь среды 2. Поскольку преломленная волна в левой среде является обратной, ее волновой вектор будет направлен к границе раздела сред. Иными словами, в этом случае энергия уходит от границы, тогда как фазовый фронт «набегает» на нее. Аномальный ход преломлённого луча обеспечивает при этом выполнение условия , необходимого для удовлетворения граничных условий для векторов электромагнитного поля. В связи со сказанным, левые среды называют также средами с отрицательным преломлением.

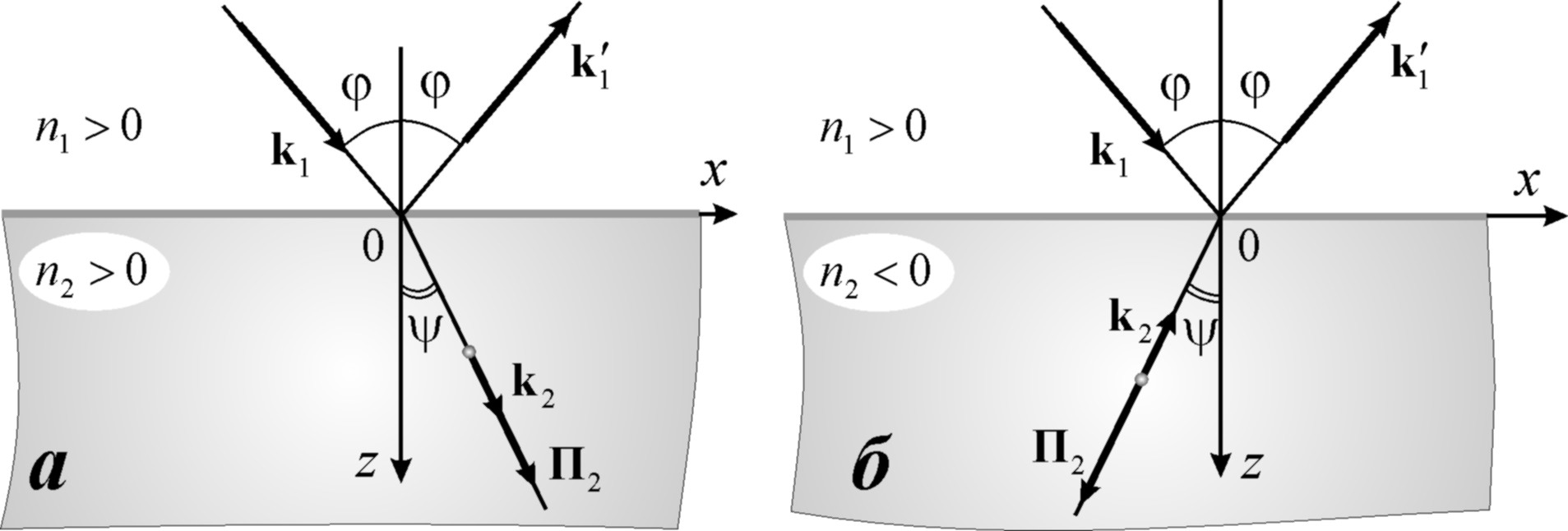
Рис. 4.4.