4. Электромагнитные волны в средах с комплексными материальными параметрами

4.1. Плоские монохроматические волны в среде с комплексными материальными параметрами

Выше, в главах 2 и 3, значения материальных констант ε и μ предполагались вещественными. Теперь рассмотрим более общий случай, когда диэлектрическая и (или) магнитная проницаемость имеют отличные от нуля мнимые части.

Записать выражение для комплексной проницаемости, например, , можно различными способами:

где и − соответственно вещественная и мнимая части комплексного числа , − его модуль, − аргумент (фаза). Аналогично можно представить и комплексную магнитную проницаемость :

Фазовые углы и комплексных проницаемостей и называют углами диэлектрических (магнитных) потерь. В справочниках часто приводят значения тангенсов диэлектрических (магнитных) потерь, т.е. величин и .

При учёте комплексности параметров и внешний вид уравнений Максвелла и их решений не изменяется. Однако теперь при анализе выражений вида (2.26), (2.27) для полей плоских монохроматических волн необходимо учесть, что:

1) становится комплексным показатель преломления

и, соответственно, волновое число (постоянная распространения)

2) становится комплексным импеданс (волновое сопротивление)

,

где − модуль, − фаза комплексного импеданса.

При учёте комплексности величин и выражения для компонент векторов поля плоской волны линейной поляризации, распространяющейся в положительном направлении оси z, принимают вид:

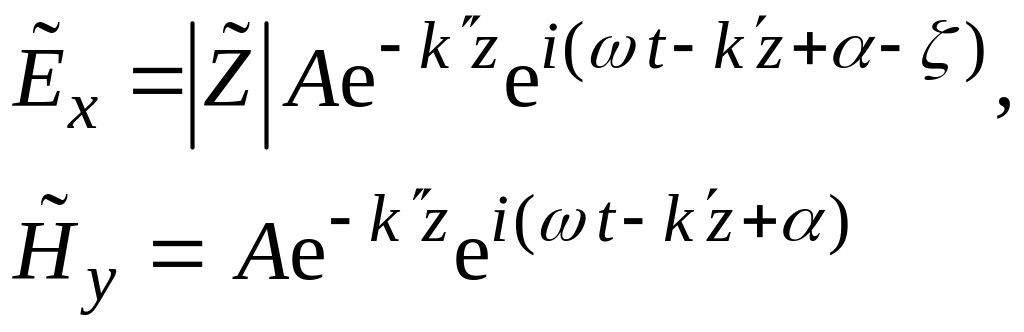
(здесь A и α − амплитуда и начальная фаза магнитного поля волны). Анализируя , приходим к следующим выводам.

1. Роль волнового числа для волны вида играет вещественная часть комплексного волнового числа , при этом выполняются соотношения

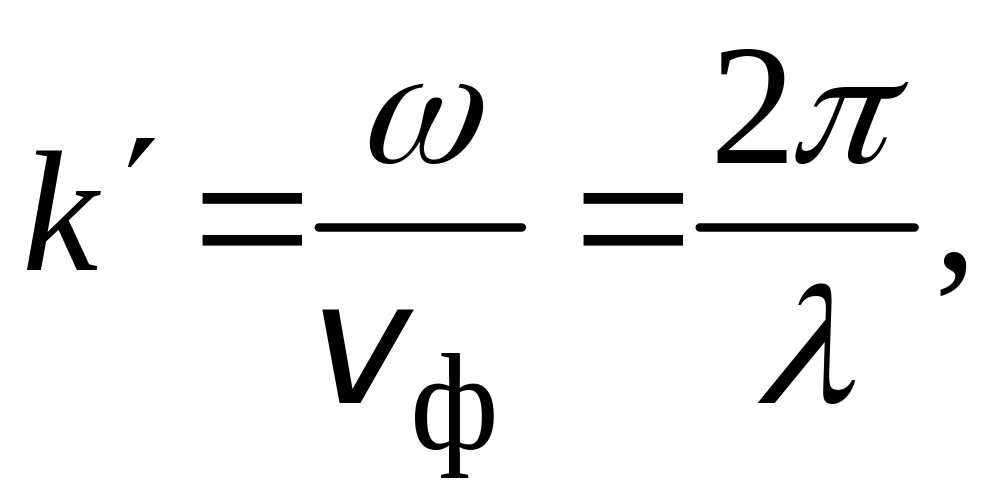
причем − длина волны в среде.

2. Амплитуда волны (выражение, стоящее перед комплексной экспонентой), оказывается зависящей от координаты z по экспоненциальному закону. При амплитуда уменьшается в направлении оси z (волна затухает), а при − увеличивается (волна усиливается). Затухание волны характерно в первую очередь для сред, обладающих потерями, где оно обусловлено переходом энергии ЭМП волны в другие формы энергии (обычно во внутреннюю). Такая среда называется поглощающей или пассивной. Усиление волны наблюдается в квантовых генераторах, среды такого типа называют усиливающими или активными (не путать с понятиями «активные компоненты полей» и «активная энергия»!). Мнимая часть называется коэффициентом затухания (усиления). Его величина обратна расстоянию , на котором амплитуда волны убывает (возрастает) в е раз.

3. Отношение амплитуд колебаний электрического и магнитного полей равно модулю комплексного импеданса среды

4. При отличии от нуля мнимой части импеданса возникает сдвиг фаз между колебаниями электрического и магнитного векторов, равный фазе комплексного импеданса . Величина сдвига фаз играет существенную роль в процессах переноса энергии электромагнитной волной.

Итак, комплексность материальных констант влечёт за собой затухание или усиление электромагнитной волны, а также рассогласование фаз колебаний векторов Е и Н.

Далее будут рассматриваться только пассивные среды, в которых имеет место затухание электромагнитных волн (оно не обязательно связано с потерями!). Как будет показано ниже, для пассивных сред углы потерь должны быть ПОЛОЖИТЕЛЬНЫМИ, если изображать комплексные числа , точками координатной плоскости. На рис. 4.1 изображена координатная плоскость , каждой точке которой соответствует определённое значение комплексной диэлектрической проницаемости . Комплексное число также может быть представлено вектором, соединяющим начало координат с соответствующей точкой плоскости; его модуль равен , а угол, который он образует с осью абсцисс − углу потерь .

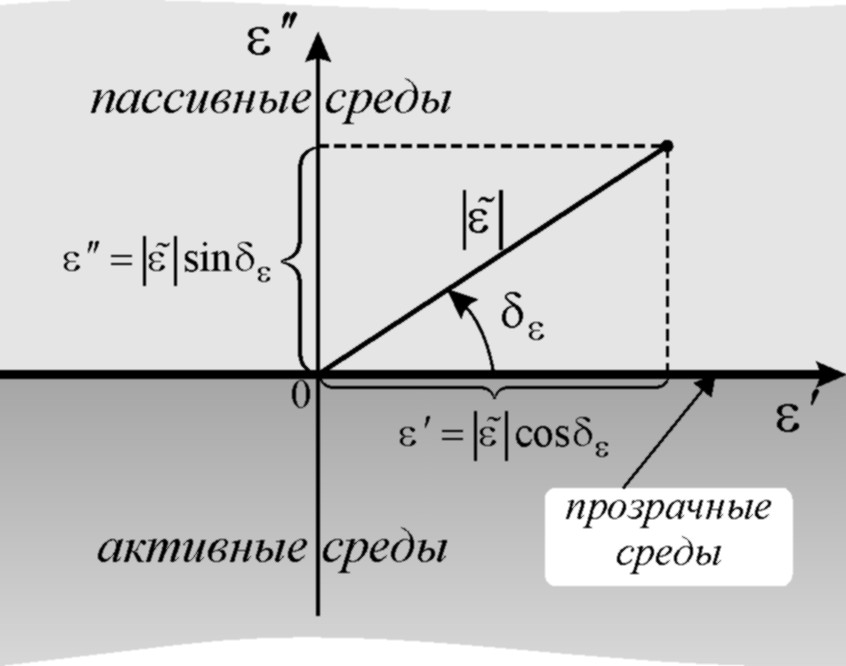
Рис. 4.1.

Пассивным средам на рис. 4.1 соответствует верхняя полуплоскость ( ), активным – нижняя ( ). Прозрачным средам без потерь (в данном случае – диэлектрических) соответствуют точки с ( ). Аналогично выглядит комплексная плоскость значений магнитной проницаемости .