3.3. Прохождение плоской волны через плоскопараллельный диэлектрический слой

Рассмотрим плоскопараллельный диэлектрический слой толщиной d. Показатель преломления вещества слоя (среда 2) обозначим , а показатели преломления окружающих его сред 1 и 3 − и . Все показатели преломления будем считать постоянными (среды однородны). Получим формулы для расчёта коэффициентов отражения и прохождения электромагнитной волны, падающей на слой из среды 1. Ограничимся частным случаем нормального падения, при котором случаи параллельной и перпендикулярной поляризации падающей волны неотличимы друг от друга. Волновые векторы и векторы поля волн во всех трёх областях рассматриваемой структуры изображены на рис. 3.4.

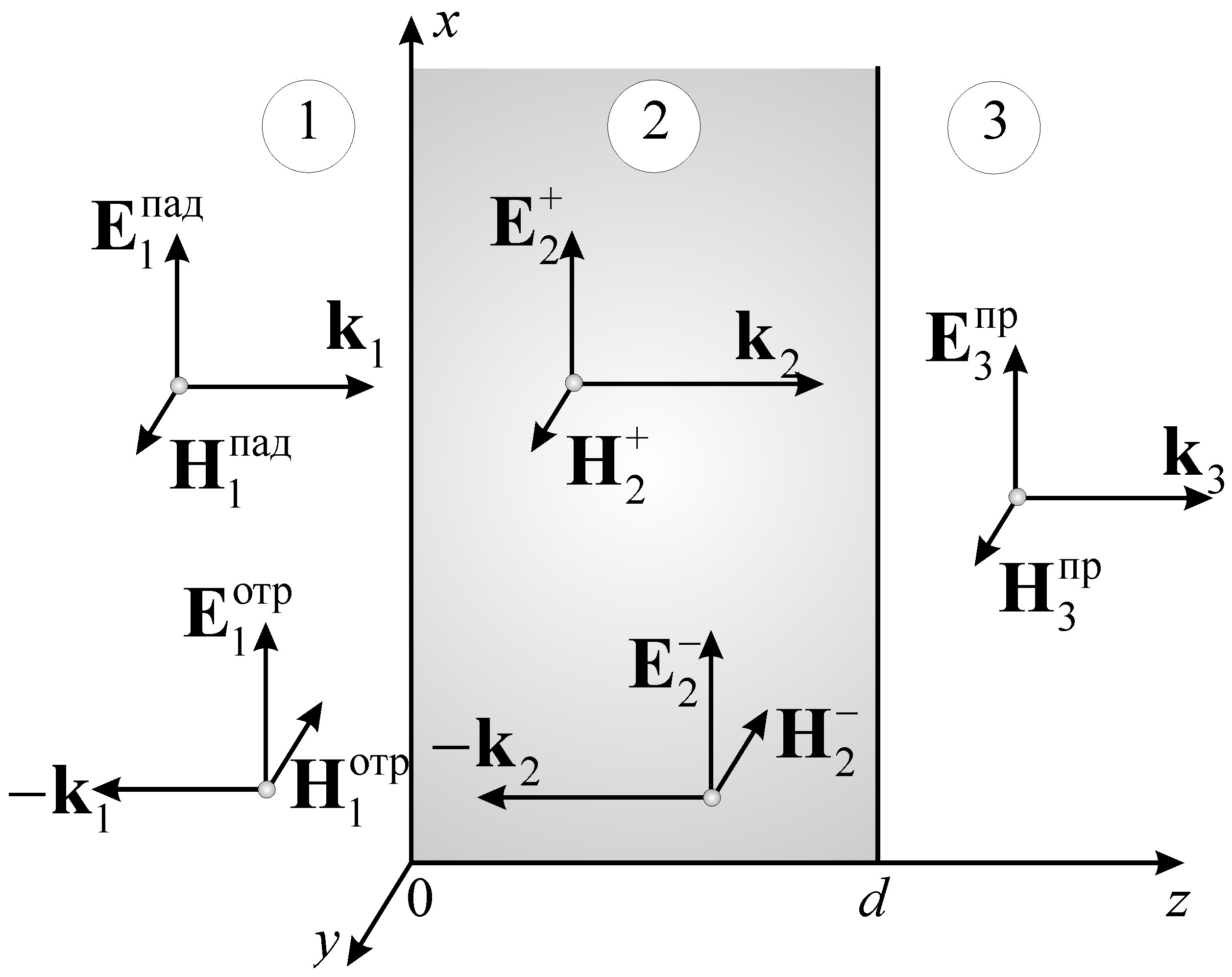
Рис. 3.4.

Векторы поля в среде 1 (z ≤ 0) записываются в виде суперпозиции падающей и отражённой волн, распространяющихся в противоположных направлениях вдоль оси z:

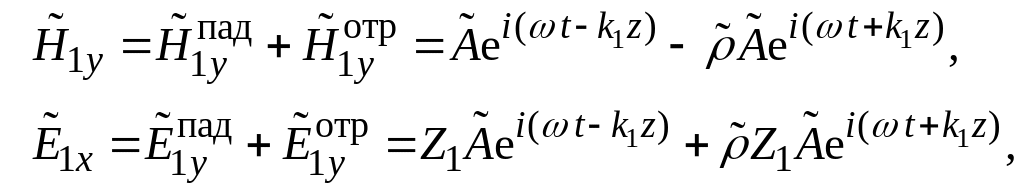
где введён комплексный коэффициент отражения . Волна внутри слоя (область 2, 0 ≤ z ≤ d) формируется в результате многолучевой интерференции: её поле является суммой полей бесконечного числа парциальных волн, возникающих при многократных отражениях от поверхностей слоя. Формально это поле можно, как и для среды 1, записать в виде суперпозиции двух встречных волн:

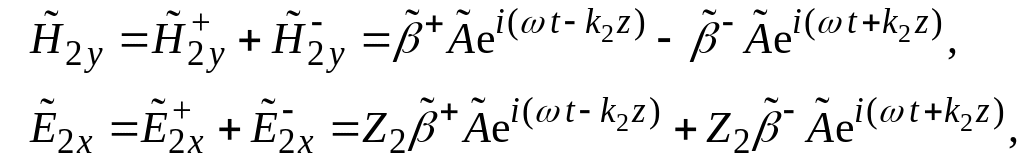
где − подлежащие определению комплексные коэффициенты. Наконец, в области 3 (z ≥ d) существует одна прошедшая через слой волна:

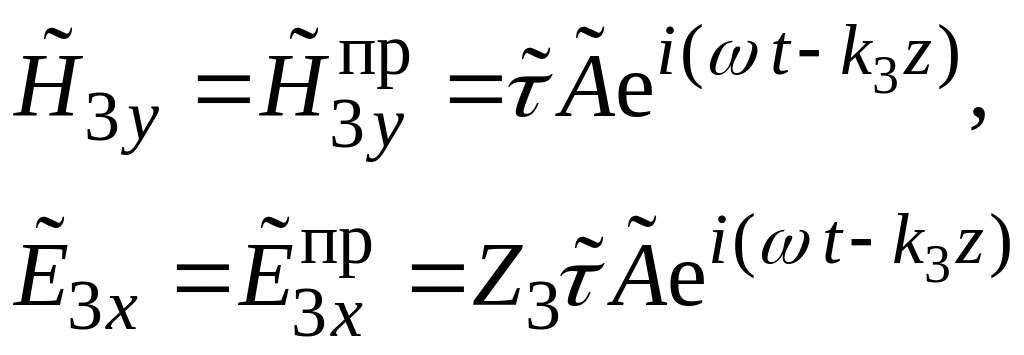
( − комплексный коэффициент прохождения по магнитному полю).

Для нахождения коэффициентов и используются граничные условия (1.19) и (1.17) для векторов магнитного и электрического поля. Их следует записать дважды − для границ раздела сред z = 0 и z = d:

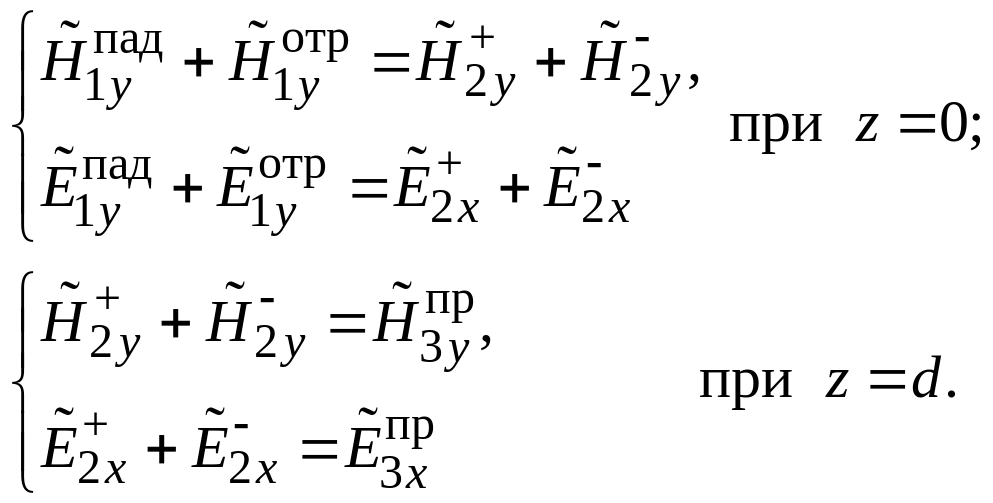
Подставляя в выражения для проекций векторов поля − , получаем систему уравнений:

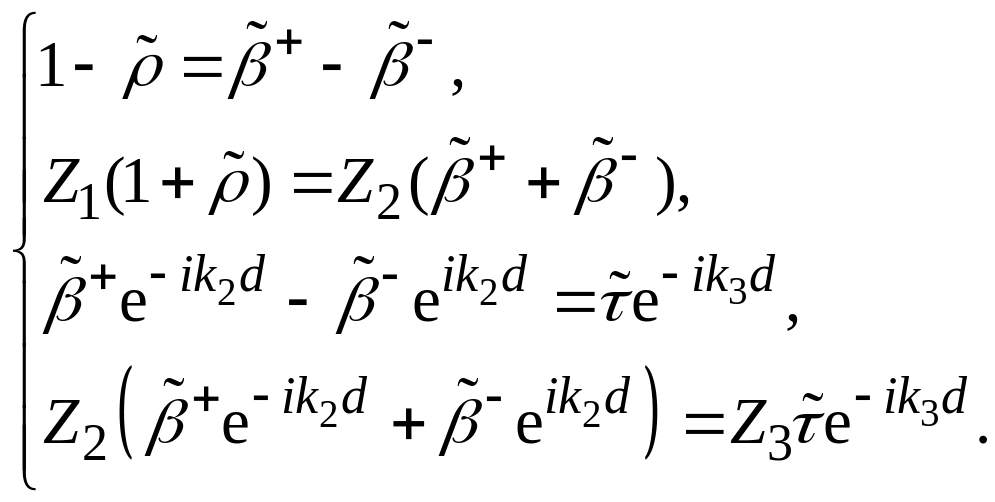
Исключая из системы коэффициенты и , получаем искомые выражения для и :

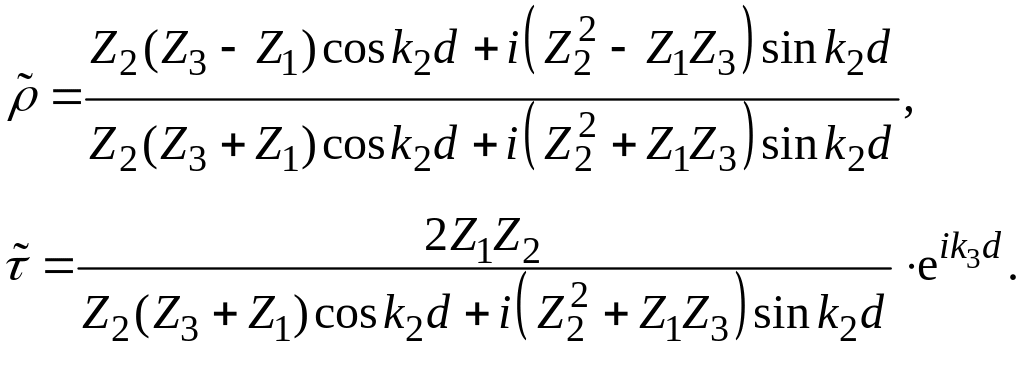
Коэффициент в определён как коэффициент прохождения по магнитному полю. Коэффициент прохождения по электрическому полю связан с ним соотношением . Представляя комплексные коэффициенты в виде , можно определить амплитуды и фазы отражённой и прошедшей через слой волн.

Из формул видно, что коэффициенты отражения и прохождения являются периодическими функциями толщины слоя d. Не вдаваясь в подробности, отметим некоторые частные случаи. Прежде всего, установим условия полного прохождения энергии падающей волны через слой, т.е. когда коэффициент отражения обращается в нуль.

Случай 1. Если где N = 1, 2, 3…, т.е. толщина слоя принимает ряд значений , то , и коэффициент отражения равен

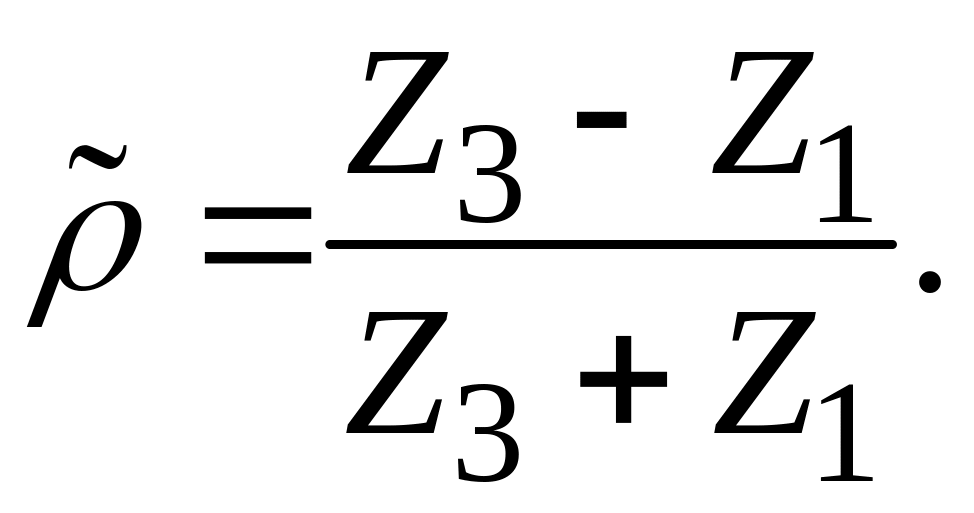
Если слой граничит с одинаковыми средами, то и  = 0. Данный случай хорошо известен в оптике как «слой толщиной в полволны» или «полуволновая пластинка (плёнка)». Выражение совпадает с формулой коэффициента отражения от одиночной границы раздела сред с импедансами и (см. формулы Френеля и ).

Случай 2. Пусть где N – нечётное целое число (N = 1, 3, 5…), т.е. («слой в четверть длины волны», «четвертьволновая пластинка»). Тогда , и

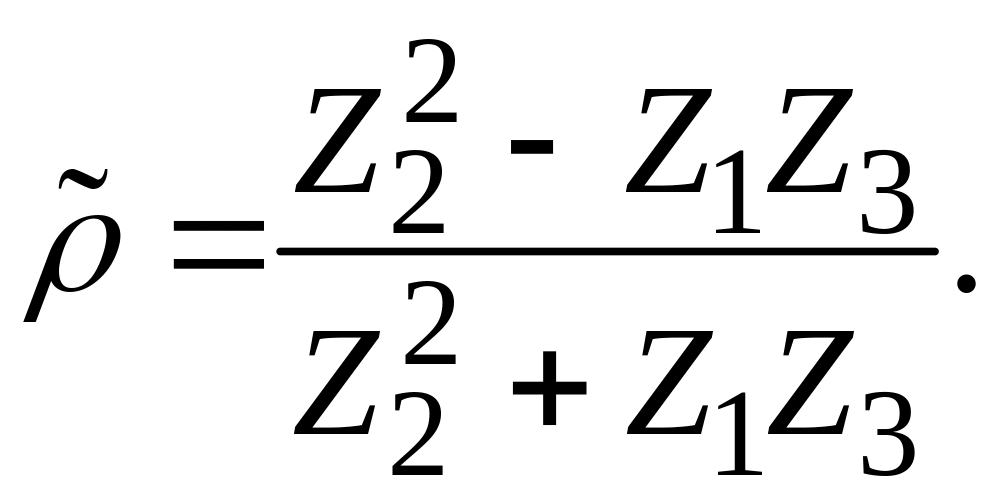
В данном случае коэффициент отражения обращается в нуль при выполнении условия

Для немагнитных сред (μ = 1) (n – показатель преломления среды) и условие записывается как . Полученный результат используется при нанесении на поверхности просветляющих покрытий с целью уменьшения отражательной способности. Толщина просветляющего покрытия должна составлять четверть длины волны, а его материальные параметры должны обеспечивать выполнение условия .