3.2. Полное внутреннее отражение

Рассмотрим закон Снеллиуса в случае, когда среда 2 является оптически менее плотной, чем среда 1 ( ). Тогда и поэтому найдётся критическое значение угла падения , при котором угол преломления достигает своего предельного значения  = 90º, т.е. преломлённая волна распространяется вдоль границы раздела:

При преломлённой волны в обычном смысле не существует, и вся энергия падающей волны полностью возвращается в первую среду. Описанное явление называют полным внутренним отражением, а угол − углом полного внутреннего отражения.

Рассмотрим структуру поля в средах 1 и 2 при полном внутреннем отражении (на примере его электрической составляющей). Систему координат введём так же, как и на рис. 3.1 и 3.2. Поле в среде 1 представляет собой суперпозицию падающей и отражённой волн:

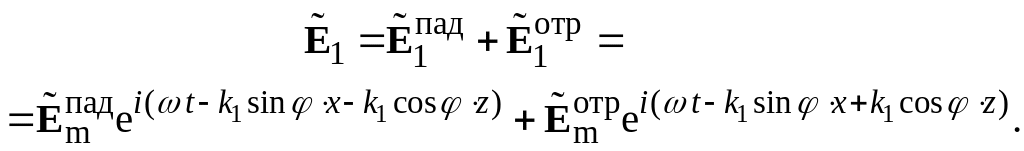
При полном отражении амплитуды падающей и отраженной волн равны по модулю, но отличаются фазовым множителем . При этом приводится к виду

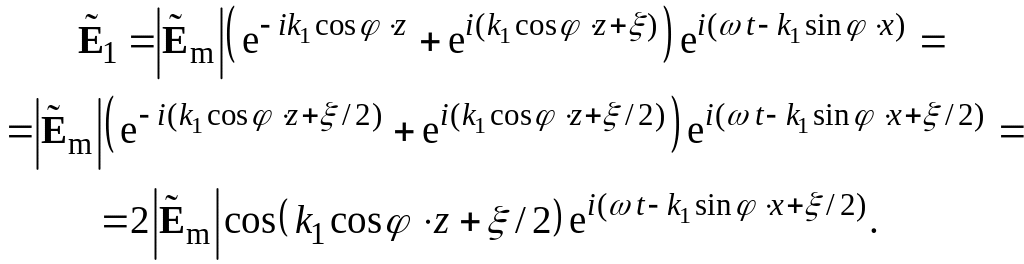
Из следует, что в среде 1 в направлении оси x распространяется бегущая волна с фазовой скоростью

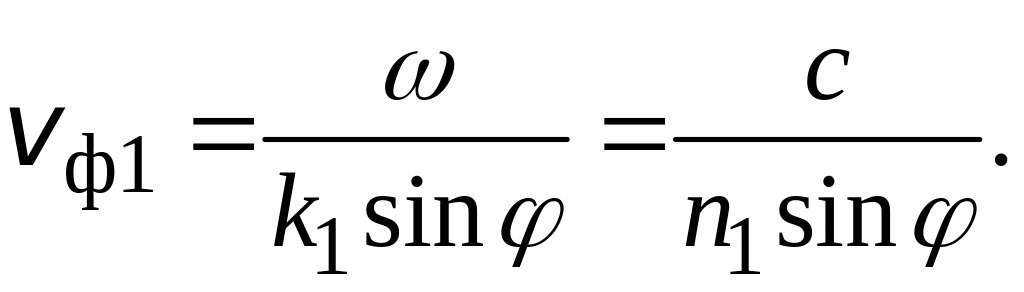
Амплитуда этой волны гармонически зависит от координаты z; это означает, что в направлении оси z поле представляет собой стоячую волну с чередованием минимумов (узлов) и максимумов (пучностей).

Несмотря на полное отражение, электромагнитное поле присутствует и в среде 2. Запишем его формально как обычную преломлённую волну:

При полном отражении , что невозможно, если угол преломления ψ считать вещественным. Однако синус комплексного аргумента может принимать любые значения. Косинус угла ψ будет при этом мнимой величиной:

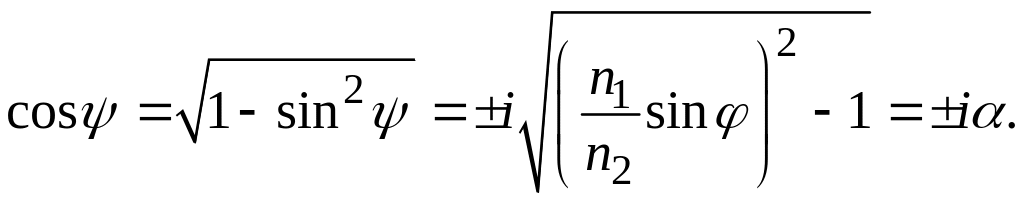
Подставляя выражения для sin ψ и cos ψ в , получим:

Источники поля находятся в среде 1, поэтому при удалении от границы раздела вглубь среды 2 амплитуда преломлённой волны может только убывать. Значит, в показателе первой экспоненты в следует выбрать знак «минус» (при условии, что ). Поле представляет собой волну, бегущую в направлении оси x с фазовой скоростью

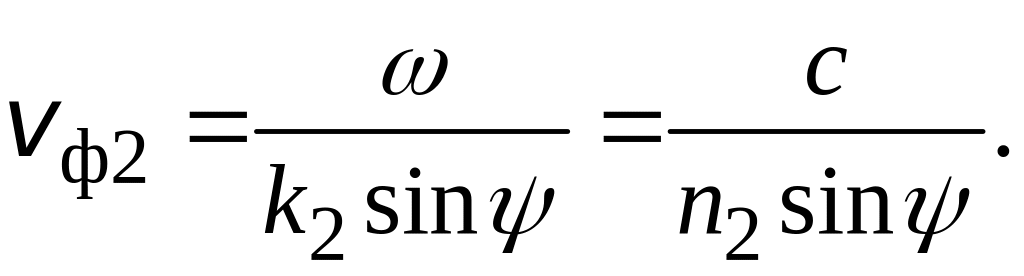
Амплитуда волны экспоненциально убывает по мере удаления от границы раздела. Таким образом, поверхности равных амплитуд волны в среде 2 представляют собой плоскости , параллельные границе раздела сред. В то же время фаза волны распространяется в направлении оси x, и поверхности равных фаз перпендикулярны границе раздела. Волну, у которой поверхности равных амплитуд не совпадают с поверхностями равных фаз, называют неоднородной.

Глубина, на которой амплитуда поля уменьшается в е раз, равна , и по порядку величины равна длине волны в среде 2. Таким образом, поле в среде 2 при полном отражении сосредоточено в достаточно тонком приповерхностном слое. В связи с этим волну данного типа, распространяющуюся параллельно границе раздела сред, называют поверхностной волной. Эту волну называют также медленной, поскольку ее фазовая скорость при распространении в направлении оси x меньше фазовой скорости при распространении соответствующей однородной волны в среде 2, равной .

Можно показать, что интенсивность (средняя плотность потока энергии) волны в среде 2 в направлении оси z равна нулю (однако при этом существует колеблющаяся составляющая вектора Пойнтинга ). Перенос энергии во среде 2 осуществляется только в направлении оси x (интенсивность отлична от нуля). Детальный анализ нестационарной задачи показывает, что поток энергии во вторую среду отличен от нуля в первые моменты времени. В результате при переходе в стационарное состояние происходит установление во второй среде описанной выше поверхностной волны.