2.8. Групповая скорость

Бегущая монохроматическая волна переносит энергию, но с её помощью нельзя передать информацию – сигнал для этого должен быть модулированным. Более того, на практике чисто монохроматическая волна не осуществима, так как должна была бы быть бесконечной - прежде всего, во времени. Реальные сигналы чаще всего являются импульсами конечной длительности. С помощью спектрального разложения в ряд или интеграл Фурье произвольный сигнал можно представить в виде суперпозиции конечного или бесконечного числа монохроматических колебаний различных частот.

Волновой процесс, образованный монохроматическими составляющими, близкими по частоте, называется группой волн или волновым пакетом. Рассмотрим простейший волновой пакет, имеющий всего две монохроматических волны с одинаковыми амплитудами и различными, но близкими друг другу частотами и и волновыми числами и , т.е.

где .

Мгновенные значения напряжённости электрического поля данного сигнала можно записать в виде

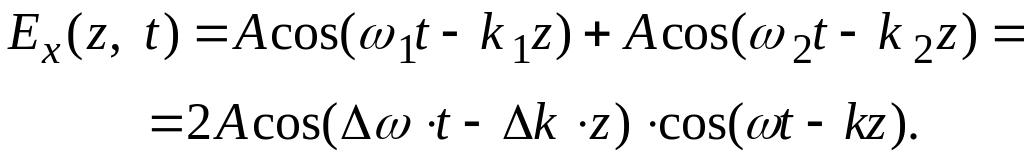
Данный процесс можно рассмотреть как монохроматическое колебание средней частоты ω, но с модулированной амплитудой, достаточно медленно изменяющейся во времени по гармоническому закону

(частота изменения амплитуды ). Другими словами, процесс носит характер биений. Функция – это уравнение огибающей высокочастотного сигнала.

Скорость переноса энергии группой волн (групповую скорость) найдём как скорость некоторой фиксированной точки огибающей сигнала. Положим  = const и найдём отсюда групповую скорость как

Переходя к пределу Δω → 0, окончательно найдём

Для расчета групповой скорости необходимо знать соотношение между частотой ω и волновым вектором k в виде зависимости ω(k) или k(ω), которую называют законом дисперсии или дисперсионным уравнением.

Найдём групповую скорость плоской волны. С учётом и

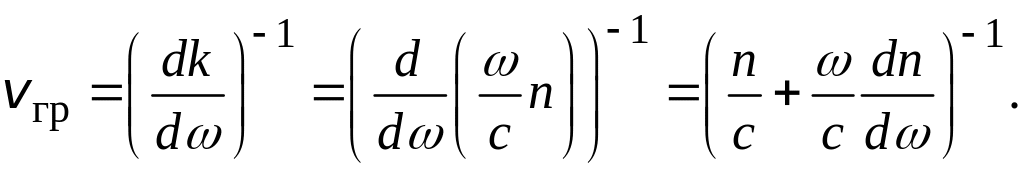
Если показатель преломления n не зависит от частоты ω, то групповая скорость равна фазовой:

Если n и, как следствие, фазовая скорость волны являются функциями частоты ω, то говорят, что среда обладает частотной дисперсией. В этом случае фазовая и групповая скорости различны. Их связь выражается формулой

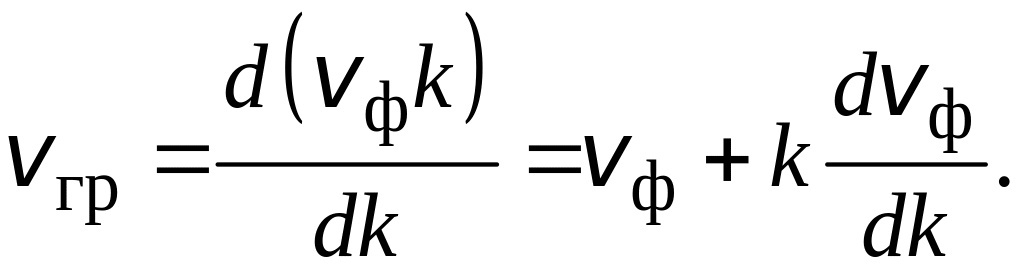
Учитывая, что k =2π/λ, можно привести к виду

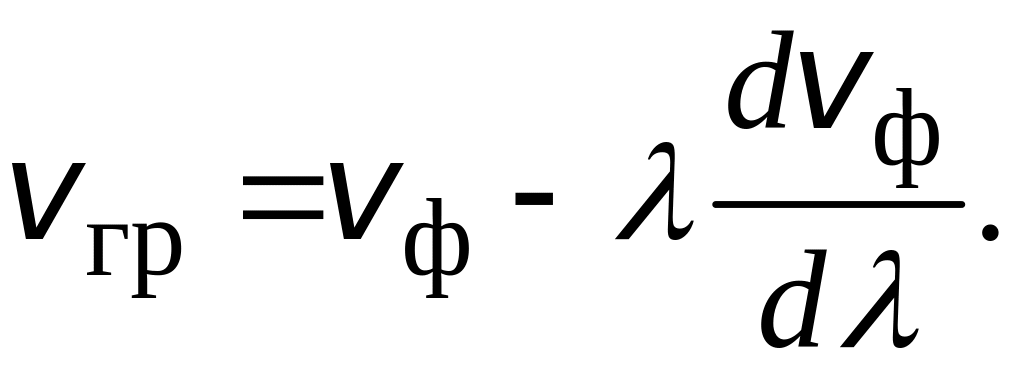
Соотношение называют формулой Рэлея. Из неё видно, что фазовая и групповая скорости не только отличаются по величине, но могут также различаться и знаками. В анизотропных средах векторы фазовой и групповой скорости обычно не совпадают по направлению.

Групповая скорость характеризует перемещение в пространстве возмущения фиксированной амплитуды; поскольку с амплитудой связана энергия волны, то групповая скорость определяет скорость и направление переноса энергии волной. В соответствии с теорией относительности, групповая скорость не может превышать скорости света в вакууме c. Напротив, фазовая скорость является абстрактным понятием и не связана с переносом в пространстве чего-то материального; поэтому её величина может быть больше c.

Понятие групповой скорости применимо, когда потери малы и дисперсия является слабой. Если фазовые скорости различных составляющих сигнала будут сильно отличаться друг от друга, то со временем импульс будет «расплываться» и его огибающая будет терять свою форму. Проследить за движением какой-либо точки огибающей при этом невозможно, и понятие групповой скорости теряет свой смысл.