2.7. Стоячие электромагнитные волны

Рассмотрим суперпозицию двух волн одинаковой частоты и амплитуды, распространяющихся навстречу друг другу в однородном изотропном диэлектрике без потерь. Обычно такая ситуация возникает при полном отражении падающей волны от границы раздела сред. Для волн СВЧ диапазона такой границей может служить поверхность металла.

Суммарное поле системы двух встречных волн запишем в вещественной форме:

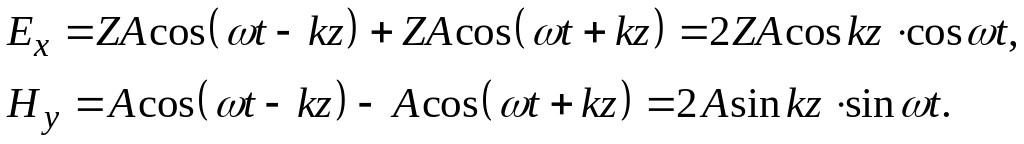
Запись предполагает, что начальные фазы обеих волн одинаковы и равны нулю. Это упрощает запись формул и несущественно для дальнейшего изложения.

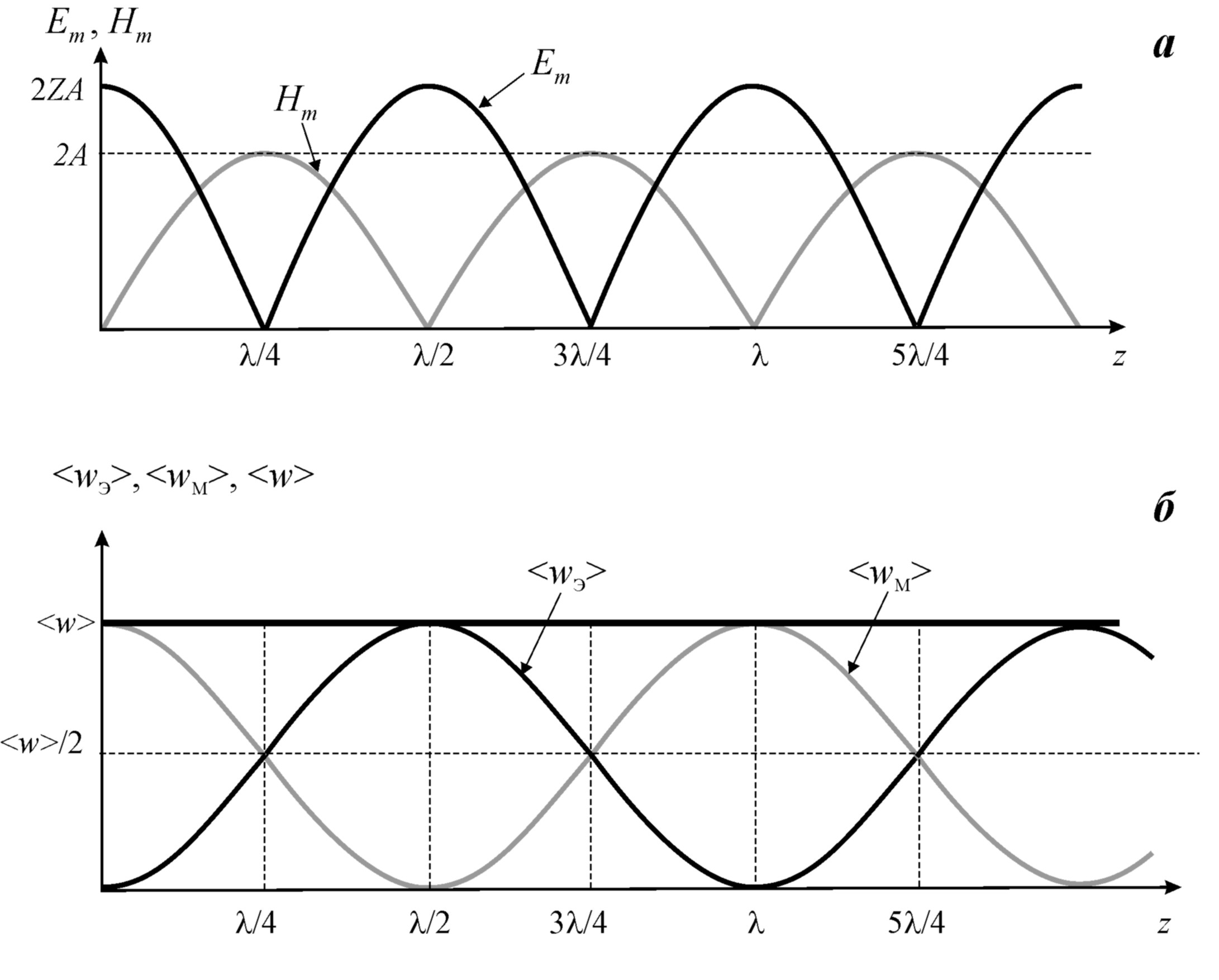
Рис. 2.5.

Из видно, что суммарное поле представляет собой гармоническое колебание частоты ω. Однако электрическое поле изменяется по закону косинуса, а магнитное – синуса, что говорит о сдвиге фаз колебаний векторов поля, равном π/2.

Амплитуды колебаний электрического и магнитного полей

периодически зависят от координаты z. На оси z можно выделить узлы – точки, в которых амплитуда поля равна нулю, и пучности, в которых амплитуда максимальна (рис. 2.5а). Узлы и пучности отстоят по оси z друг от друга на расстоянии λ/2 (λ – длина волны), причём пучности располагаются посередине между соседними узлами. При этом в узлах электрического поля располагаются пучности магнитного и наоборот. Положения узлов и пучностей на оси z неизменны, поэтому колебательный процесс данного типа называют стоячей волной.

Вектор Пойнтинга стоячей волны имеет только одну z-компоненту:

Видно, что поток энергии стоячей волны имеет только колеблющуюся составляющую, а его среднее значение (интенсивность) равно нулю. Таким образом, в отличие от бегущей волны, стоячая волна не переносит энергии. Это объясняется наличием узлов – точек, в которых одно из полей неизменно равно нулю.

Плотность энергии электрического и магнитного полей стоячей волны имеет вид:

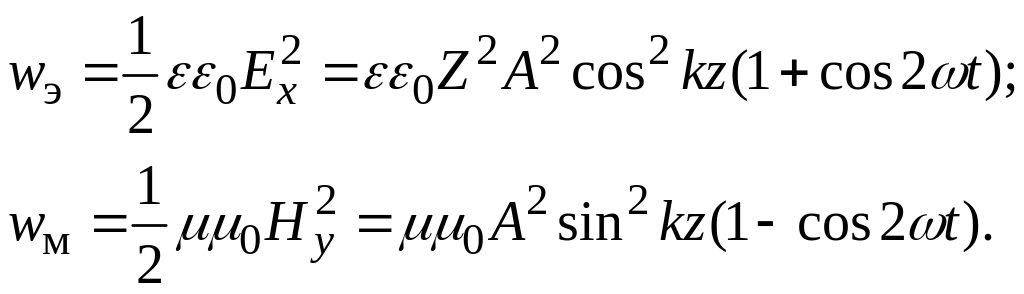
Видно, что и колеблются около средних значений

которые отличны от нуля, но не равны друг другу, как в бегущей волне, поскольку различным образом зависят от координаты z (рис.2.5б). Максимумы приходятся на пучности электрического, а максимумы − на пучности магнитного поля, которые разнесены в пространстве. В то же время суммарная средняя плотность энергии является постоянной величиной:

Итак, стоячая волна обладает некоторым запасом электромагнитной энергии, которая, однако, не вовлекается в процесс переноса. Эту энергию называют реактивной в отличие от «активной» энергии бегущей волны, переносящей энергию в пространстве. Обращаем внимание на причину такого различия: в бегущей волне колебания векторов поля синфазны, а в стоячей волне сдвиг фаз составляет π/2.

Перенос энергии стоячей волной является локальным, ограниченным пространственной ячейкой длиной λ/4 между двумя соседними узлами – узлом электрического и узлом магнитного поля. В течение половины периода колебаний энергия переносится, например, от пучности электрического поля к пучности магнитного, превращаясь при этом из электрической в магнитную. В течение следующей половины периода энергия переносится в противоположном направлении, испытывая обратное превращение. Аналогичные взаимные превращения электрической и магнитной составляющих реактивной энергии имеют место в цепях переменного тока.