12) Условия на границе двух диэлектриков для векторов b и d

Два соприкасающихся диэлектрика с различными диэлектрическими проницаемостями ε₁ и ε₂, помещенные во внешнее электрическое поле.

Прямоугольный контур a×b

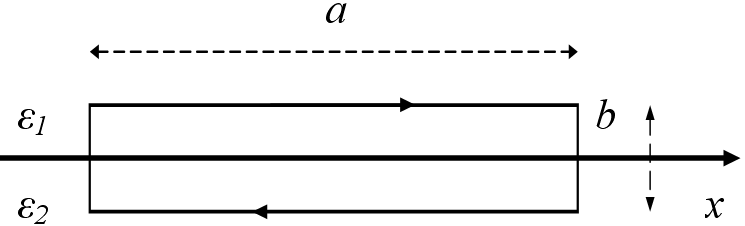
Циркуляция вектора Е по замкнутому контуру =>

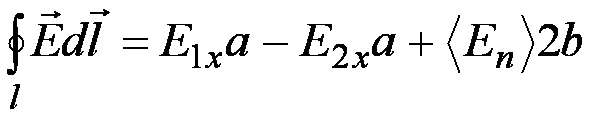
E_1x= E _1τ , E_2x= E_2τ – тангенциальные составляющие вектора Е в 1 и 2 диэлектрике, соответственно.

‹E_n› – среднее значение E_l на участках контура перпендикулярных к границе.

=> Сторона b контура мала: b→0. =>

Возьмем на границе цилиндрическую поверхность высотой h. Основание S₁ расположено в первом диэлектрике, S₂ – во втором диэлектрике.

S₁ = S₂  = S → 0. Поле в пределах S - однородное. Сторонних зарядов на границе 2-х диэлектриков нет =>

D_1n – проекция вектора D в первом диэлектрике на нормаль n₁,

D_2n – проекция вектора D во втором диэлектрике на нормаль n₂,

‹D_n› – значение D_n, усредненное по всей боковой поверхности.

Если рассмотреть проекции векторов D₁ и D₂ на одну и ту же нормаль

13) Намагничение вещества, намагниченность j.

Экспериментальные исследования показали, что все вещества в большей

или меньшей степени обладают магнитными свойствами. Если два

витка с токами поместить в какую-либо среду, то сила магнитного

взаимодействия между токами изменяется. Этот опыт показывает, что

индукция магнитного поля, создаваемого электрическими токами в

веществе, отличается от индукции магнитного поля, создаваемого теми

же токами в вакууме. Магнитные свойства веществ определяются

магнитными свойствами атомов или элементарных частиц (электронов,

протонов и нейтронов), входящих в состав атомов.

Вещества крайне разнообразны по своим магнитным свойствам. У

большинства веществ эти свойства выражены слабо.

Слабо-магнитные вещества делятся на две большие группы –

парамагнетики и диамагнетики.

Вещества, способные сильно намагничиваться в магнитном поле,

называются ферромагнетиками.

При описании магнитного поля в веществе –магнетите можно, не вдаваясь в природу этих элементарных токов, для простоты считать их все одинаковыми.

Пусть каждая молекула вещества характеризуется некоторым магнитным моментом pm = I_мол*S_мол*n

Количественной характеристикой намагниченного состояния вещества

служит векторная величина намагниченность J, равная отношению

магнитного момента pm макроскопически малого объёма дельта V вещества к этому объему:

Аналогично тому, как это было сделано для поляризованности Р,

намагниченность можно выразить как

Намагничивание приводит к преимущественной ориентации магнитных моментов молекул. То же самое можно сказать и об элементарных токах. Преимущественная ориентация элементарных токов приводит к возникновению макроскопических токов – токов намагничивания. Обычные токи, связанные с перемещением в веществе носителей тока называются токами проводимости.

14) Циркуляция вектора j

Оказывается, что для стационарного случая циркуляция намагниченности

J по произвольному замкнутому контуру равна алгебраической сумме

токов намагничивания I’, охватываемых контуром:

В магнетиках, помещенных во внешнее магнитное поле, возникают токи

намагничивания, поэтому циркуляция вектора В определяется не только

токами проводимости, но и токами намагничивания:

Однако оказывается можно найти вспомогательный вектор, циркуляция

которого определяется только токами проводимости, охватываемыми

контуром. Проведем следующие преобразования: