1) Поле в. Сила Лоренца.
где
– магнитная постоянная;
- диэлектрическая постоянная = 8.85*10-12
К²/Н*м²
Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.
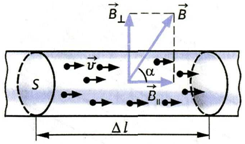
Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца.
Сила Лоренца определяется соотношением: Fл = q·V·B·sin a
где q - величина движущегося заряда;
V - модуль его скорости;
B - модуль вектора индукции магнитного поля;
a - угол между вектором скорости заряда и вектором магнитной индукции.
Обратите внимание, что сила Лоренца перпендикулярна скорости и поэтому она не совершает работы, не изменяет модуль скорости заряда и его кинетической энергии. Но направление скорости изменяется непрерывно
Сила Лоренца перпендикулярна векторам В и v , и её направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку расположить так, чтобы составляющая магнитной индукции В, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца F л.
Сила
Лоренца зависит от модулей скорости
частицы и индукции магнитного поля. Эта
сила перпендикулярна скорости и,
следовательно, определяет центростремительное
ускорение частицы. Частица
равномерно движется по окружности
радиуса r.
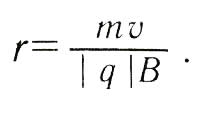
2) Закон Био-Савара.
Магнитное поле, создаваемое несколькими движущимися зарядами, равно векторной сумме магнитных полей, создаваемых каждым из зарядов.
где
– магнитная постоянная;
- диэлектрическая постоянная = 8.85*10-12
К²/Н*м²
3) Циркуляция и поток вектора в.
Циркуляция
вектора В по произвольному замкнутому
контуру равна произведению
на алгебраическую сумму токов, хватывающих
контур.
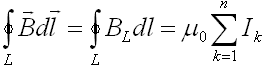
где
– магнитная постоянная;
- диэлектрическая постоянная = 8.85*10-12
К²/Н*м²
Циркуляция В не равна нулю и это означает, что магнитное поле является вихревым.
Потоком
вектора магнитной индукции
(магнитным
потоком)
dФ
сквозь
малую поверхность плошадью dS
называется скалярная величина
Сквозь
произвольную поверхность S
магнитный поток равен
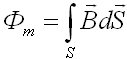
Магнитный поток сквозь произвольную замкнутую поверхность равен нулю
(теорема Остроградского-Гаусса для магнитного поля)
Этот результат означает, что в природе не существует "магнитных зарядов" – физических объектов, на которых бы начинались или заканчивались линии магнитной индукции.
4) Поле прямого тока.
Для магнитного поля тока, текущего по тонкому прямому проводнику бесконечной длины в произвольной точке, удаленной от оси проводника на расстояние R, можно записать
→
где
– магнитная постоянная;
- диэлектрическая постоянная = 8.85*10-12
К²/Н*м² ; μ
– магнитная проницаемость среды.
5) Поле солиноида.
Применим
теорему о циркуляции вектора
для вычисления простейшего магнитного
поля – бесконечно длинного соленоида,
представляющего собой тонкий провод,
намотанный плотно виток к витку на
цилиндрический каркас (рис. 2.11).
Рис. 2.11
Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью.
Бесконечно
длинный соленоид симметричен любой,
перпендикулярной к его оси плоскости.
Взятые попарно (рис. 2.12), симметричные
относительно такой плоскости витки
создают поле, в котором вектор
перпендикулярен плоскости витка, т.е.
линии магнитной индукции имеют направление
параллельное оси соленоида внутри и
вне его.
Рис. 2.12
Из
параллельности вектора
оси соленоида вытекает, что поле как
внутри, так и вне соленоида должно быть
однородным.
Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде, как показано на рисунке 2.13.
Рис. 2.13
Второй
и четвёртый интегралы равны нулю, т.к.
вектор
перпендикулярен направлению обхода,
т.е
.
Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда
где
– магнитная индукция на участке 1–2 –
внутри соленоида,
– магнитная проницаемость вещества.
Если отрезок 1–2 внутри соленоида, контур охватывает ток:
где
n – число витков на единицу длины, I –
ток в соленоиде (в проводнике).
Тогда
магнитная индукция внутри
соленоида:
Вне
соленоида:
и
, т.е.
.