Рефлексивное отношение

В математике бинарное отношение   на множестве   называется рефлексивным, если всякий элемент этого множества находится в отношении   с самим собой.

Формально, отношение   рефлексивно, если  .

Свойство рефлексивности при заданных отношениях матрицей характеризуется тем, что все диагональные элементы матрицы равняются 1; при заданных отношениях графом каждый элемент имеет петлю — дугу (х, х).

Если это условие не выполнено ни для какого элемента множества  , то отношение   называется антирефлексивным.

Если антирефлексивное отношение задано матрицей, то все диагональные элементы являются нулевыми. При задании такого отношения графом каждая вершина не имеет петли — нет дуг вида (х, х).

Формально антирефлексивность отношения   определяется как:  .

Если условие рефлексивности выполнено не для всех элементов множества  , говорят, что отношение   нерефлексивно.

Примеры рефлексивных отношений

• отношения эквивалентности:

  • отношение равенства 

  • отношение сравнимости по модулю

  • отношение параллельности прямых и плоскостей

  • отношение подобия геометрических фигур;

• отношения нестрогого порядка:

  • отношение нестрогого неравенства 

  • отношение нестрогого подмножества 

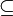
  • отношение делимости 

В математике бинарное отношение   на множестве X называется симметричным, если для каждой пары элементов множества   выполнение отношения   влечёт выполнение отношения  .

Формально, отношение   симметрично, если  .

Антисимметричность отношения не является антонимом симметричного отношения. Оба свойства для некоторых отношений выполняются одновременно, а для некоторых не выполняется ни одно.

Примеры

Любое отношение эквивалентности, по определению, является симметричным (а также рефлексивным и транзитивным). Также симметрично отношение связи вершин графа (неориентированного).

Не являются симметричными (за исключением случая тождественной ложности отношения) отношения порядка (как полного, так и частичного), а также отношение следования вершин ориентированного графа. Однако, отношение сравнимости для частичного порядка является, по построению, симметричным (хотя, в отличие от самого́ порядка, не транзитивным).

Матрица симметричного отношения симметрична относительно главной диагонали (совпадает с транспонированной). Если в графе симметричного отношения существует связь между двумя вершинами, то существует и обратная связь.

Транзитивность

В математике бинарное отношение   на множестве   называется транзитивным, если для любых трёх элементов множества   выполнение отношений   и   влечёт выполнение отношения  .

Формально, отношение   транзитивно, если  .

Примеры

• Равенство: 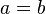  и  , значит   (на самом деле, отношение равенства вместе с отношением эквивалентности и параллельности прямых обладает более сильным свойством также ещё и «равенства третьему» по причине своей симметричности)

• Отношение порядка: 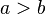  и  , значит 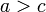  или нестрогого порядка:   и  , значит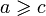 

• Параллельность прямых:   и  , значит   (см. примечание к «равенству чисел»)

• Импликация: 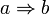  и  , значит 

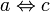• Эквивалентность:   и  , значит   (см. примечание к «равенству чисел»)

• Включение подмножества: если b является подмножеством a, и в свою очередь c является подмножеством b, тогда c является подмножеством a

• Делимость: если a делится на b, и b делится на c, тогда a делится на c.

• Отношение следования вершин ориентированного графа: если вершина 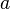  достижима из вершины  , а вершина  , в свою очередь, — из  , то   достижима из  .

Примеры отсутствия транзитивности (встречаются, когда логические высказывания связаны не арифметическими отношениями или их эквивалентами в языке, а другими смысловыми отношениями):

• Игра «Камень, ножницы, бумага»: Камень сильнее Ножниц; Ножницы сильнее Бумаги; однако Камень не сильнее Бумаги ( ). Здесь "сильнее" не имеет буквального значения, поскольку "сила" Бумаги в том, что она просто обертывает Камень.

• В круговом турнире часто бывает ситуация, когда команда A победила команду B, команда B — команду C, а C — A. Следовательно, в таком турнире отношение «победа» является нетранзитивным и не имеет эквивалента арифметической операции или арифметического отношения.

• Отношение связи вершин граф-схемы алгоритма: например, если в граф-схеме алгоритма имеет место альтернативное ветвление, начинающееся условной вершиной 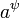 , и две вершины   и  , входящие в состав различных альтернативных ветвей ветвления, то вершина   связана с  ,   связана с  , однако вершины   и   не связаны (они либо параллельны, либо альтернативны).

• Отношение параллельности вершин параллельной граф-схемы алгоритма: например, если в составе параллельного фрагмента алгоритма в одной из ветвей находится вершина  , а другая представлена альтернативным ветвлением с двумя ветвями, одна из которых содержит вершину  , а другая — 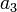 , то вершины   и   находятся в отношении параллельности, также как и вершины   и  , однако вершины   и   не параллельны (они находятся в отношении альтернативы).

• Отношение альтернативы вершин граф-схемы алгоритма: например, если в составе альтернативного фрагмента алгоритма одна из ветвей представлена вершиной  , а другая включает последовательно выполняемые вершины   и  , то вершины   и   находятся в отношении альтернативы, что справедливо и для вершин   и  , однако вершины   и   не состоят в отношении альт

11. Отношение эквивалентности. Определение фактор множества по отношению эквивалентности. Примеры.