3. Устойчивость системы автоматического регулирования

3.1 Понятия и условия устойчивости

При оценке свойств спроектированной САР прежде всего определяют ее устойчивость. Система устойчива, если после прекращения внешнего воздействия она по истечении некоторого времени возвращается к тому состоянию равновесия или вынужденного движения, в котором находилась до начала воздействия. Дорф и Бишоп («Современные системы управления», 2002г.) определяют устойчивую систему как динамическую систему, обладающую ограниченной реакцией на ограниченный входной сигнал. Наконец можно дать и другое определение : устойчивость линейной системы – это свойство затухания ее переходных процессов.

Необходимое и достаточное условие того, чтобы замкнутая система была устойчива, состоит в том, чтобы все плюсы передаточной функции системы имели отрицательные действительные части (т.е. лежали в левой компл. полуплоскости).

3.2 Критерии устойчивости

Подразделяются на алгебраические (Гурвица, Рауса) и частотные (Михайлова, Найквиста).

Критерий Рауса

1. По коэффициентам характеристического полинома R(S)=a₀sⁿ+ a₁s^n-1+…+ a_n-1s+a_n (W_замкн.=Y(S)/R(S))

Составляется таблица Рауса:

c11=a0	c11=a0	…	c1,m-1=an	c1,m=0
n+1 строка c21=a1	c22=a0	…	c2,m-1=0	c2,m=0
c31 …
cn+1,1	cn+1,2			cn+1,m

1-я строка – коэффициенты с четными индексами. Последний элемент 0.

2-я строка – коэффициенты с нечетными индексами. Если n-нечетное, то 0 ставится на место только последнего элемента. Если n-четное, то 0 ставится на места последнего и предпоследнего элементов 2-й строки (как на рис.) остальные элементы вычисляются по формуле:

C_ik=C_i-2,k+1 – D_ic_i-1,k+1, D_i= (C_i-2,1)/( C_i-1,1)

i= 3,4,…,n+1; k=1,2,…,m-1

Ci-2,1				Ci-2,k+1
Ci-1,1	Di x			Ci-1,k+1
	…	Cik	//

D_i =

Критерий Рауса:

Для устойчивости системы необходимо и достаточно, что бы коэффициенты 1-го столбца были положительны C_i,1>0, i=1, n+1. Если какой – либо из них отрицателен - система неустойчива , обращение в ноль коэффициента 1го столбца - система не является устойчивой (на границе устойчивости или неустойчива)

Пример:

Система с W_замкн(S)= (S+14) / (S³+S²+2S+24)

Характеристический полином

R(S)=1S³+1S²+2S+24

a₀ a₁ a₂ a₃

C_3,1<0

Таблица Рауса

1	2	0
1	24	0
2-1*24= -22	0	0
24- (1/(-22))*0= 24	0	0

Вывод: данная система неустойчива.

Критерий Михайлова

Пусть исследуемая на устойчивость система задана W_замкн.=Y(S)/R(S)), где R(S)=a₀sⁿ+ a₁s^n-1+…+ a_n-1s+a_n – n-го порядка

Для устойчивости динамической системы необходимо и достаточно, что бы при изменении  от 0 до ∞ кривая, описываемая концом вектора R(i), проходила против часовой стрелки через n – квадрантов.

Пример:

R(S)=0,0032s³+ 0,18s²+s+2,38 заменяем Si

R(i) =0,0032i³ ³ +0,18i² ² +i  +2,38

Поскольку i²=-1 то R(i) =-0,0032i³ ³ -0,18i² ² +i  +2,38= (2,38-0,18²)+i(-0,0032³)

Действительная часть U() мнимая V()

U()=2,38-0,18 ² V()=-0,0032 ³

=0: U(0)=2,38 : V(0)=0

=∞: U(∞)= -∞ : V(∞)= -∞

Точки пересечения годографа Михайлова и оси U() = 2,38 – 0,18² =0 => =2,38/0.18  3,6

Оцени V(3,6)3,6-0,0032*3,6³  3,48

Точки пересечения годографа Михайлова и оси абсцисс Точки пересечения годографа Михайлова и оси абсцисс V()=0: V()=-0,0032*³=(1-0,0032²)=0 => ₁=0 и ₂= 1/0,0032  17,68

Оценим U(17,68) = 2,38 – 0,18(17,68)²= -53,87

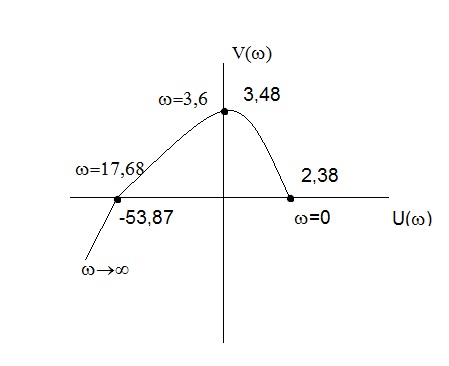
Вывод: поскольку степень характер. Полинома n=3 и годограф Михайловского проходит против час. Стрелки через 3 квадранта, то данная система устойчива.