Семестр 02 / Шпоры по физике 2 сем / Билеты по физике / Билет 14

2. Функции распределения вероятностей для составляющих скорости молекул ид. Газа

Т. к. dw_v=f(v)dv=φ(v_x)dv_xφ(v_y)dv_yφ(v_z)dv_z → ,

где φ(v_x) – функция распределения по v_x. Вероятности того, что молекула имеет проекции скорости в интервалах (v_x, v_x+dv_x), (v_y, v_y+dv_y), (v_z, v_z+dv_z), являются независимыми, поэтому в соответствии с теоремой об умножении вероятностей независимых событий можно записать:

Отсюда получаем, что f(v)=φ(v_x)φ(v_y)φ(v_z).

Откуда 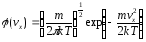. Функция нормирована на единицу. Т.е.

График зависимости φ(v_x) от v_x

_3. Теплоемкость идеального газа при постоянном объеме и при постоянном давлении.

Теплоемкостью какого-либо тела называется величи­на, равная количеству теплоты, которое нужно сообщить телу, чтобы повысить его температуру на один кельвин. Аналитически это определение записывается следующим образом: 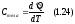Если нагревание производится при постоянном объ­еме, то тело не совершает работы над внешними телами и, cледователь- но, вся теплота идет на приращение вну­тренней энергии тела: dQ_V=dU. Отсюда следует, что молярная теплоемкость любого веще­ства при постоянном объеме равна В термодинамике подобные формулы принято записывать в виде Символ частной производной, снабженный индексом V, указывает на то, что при дифференцировании функции U_M по переменной Т объем предполагается постоянным.

Теплоемкость при постоянном давлении Ср бывает больше, чем C_V, потому что при p=const нагреваемое тело расширяется и часть подводимой теплоты расходу­ется на совершение работы над внешними телами.

Внутренняя энергия определяется с точностью до произ­вольной аддитивной постоянной. Поэтому константу в вы­ражении для U_M можно отбросить. В результате получа­ется формула Внутренняя энергия — величина аддитивная. 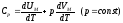Следо­вательно, внутренняя энергий массы газа m будет равна Напишем уравнение dQ=dU + pdV для моля газа, предполо­жив, что теплота сообщается газу при постоянном давле­нии: dQ_P=dU_M + pdV_M Разделив это выражение на прираще­ние температуры dT, которое получает газ при сообщении ему теплоты dQ_P, придем к формуле для молярной тепло­емкости газа при постоянном давлении: Согласно формуле (1.25) слагаемое dU_M/dT равно моляр­ной теплоемкости при постоянном объеме. Учтя это и ис­пользовав применяемый в термодинамике способ записи формул, придём к соотношению