
Семестр 02 / Шпоры по физике 2 сем / Билеты по физике / Билет 13
.pdf
1. Теплоемкость при политропичеком процессе!
2. Энергия гармонического колебания
Т.к. уравнение гармонических колебаний (уравнение гармонического осциллятора) описывает колебания совершаемые телом массы m, на которое действует только квазиупругая сила F=-kx, то это отражается и на энергии.
Квазиупругая сила является консервативной. Поэтому полная энергия гармонического колебания должна оставаться постоянной. В процессе колебаний происходит превращение кинетической энергии в потенциальную И обратно, причем в моменты наибольшего отклонения от положения равновесия полная энергия
состоит из потенциальной энергии, которая достигает своего наибольшего значения Umax:
E Umax ka22
При прохождении же системы через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в эти моменты достигает своего наибольшего значения Kmax:
|
|
|
mv 2 |
ma2 2 |
||
E K |
|
|
max |
|
0 |
|
max |
2 |
2 |
||||
|
|
|
||||
|
|
|
|
|||
Выясним, как изменяются со временем кинетическая и потенциальная энергии гармонического колебания.
Сначала найдем зависимость кинетической энергии от времени.
v x a 0 sin( 0 t ) |
||
|
|
|
|
|
|
|
K |
mx |
|
2 |
|
|
|
|
Решив данную систему из 2-ух уравнений получаем:
|
2 |
2 |
sin 2 ( |
t ) (1) |
K mx |
ma |
0 |
||
2 |
2 |
|
0 |
|
|
|
|
Потенциальная энергия выражается формулой:
U kx2 |
ka2 |
cos2 ( |
t ) (2) |
2 |
2 |
0 |
|
|
|
Сложив (1) и (2) и приняв во внимание, что m 20 k , получим формулу для полной энергии:
|
ka2 |
ma2 02 |
|
E U K |
2 |
2 |
(3) |
Таким образом, полная энергия гармонического колебания действительно оказывается постоянной. Теперь сопоставив формулы (1), (2) и (3) мы можем представить зависимость потенциальной и кинетической энергии от полной энергии гармонического колебания:
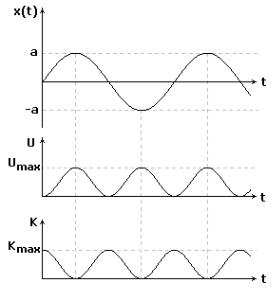
K E sin 2 ( |
t ) |
U E cos2 ( |
t ) |
0 |
|
0 |
|
|
|
|
m x |
2 |
|
k x2 |
m x |
2 (t) |
|
k x2 (t) |
|
k a2 |
|
m x |
2 |
|
|
E |
0 |
|
0 |
|
|
|
|
|
|
|
|
max |
|
||||
|
|
|
|
|
|
|
|
||||||||||
|
ïîëí |
2 |
|
|
2 |
|
2 |
|
2 |
|
2 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
m a2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

3.
