29. Каноническое уравнение гиперболы:

   Каноническое уравнение параболы: 

   Уравнения асимптот: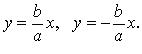 

30. Общим уравнением плоскости в пространстве называется уравнение вида

Ax + By + Cz + D = 0,

где A² + B² + C² ≠ 0 .

Рассмотрим важный частный случай построения уравнения плоскости, когда известны три точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), принадлежащие плоскости и не лежащие на одной прямой. Возьмем текущую точку M(x, y, z) плоскости и организуем три вектора

Эти векторы лежат в одной плоскости, уравнение которой и определяется. Следовательно, их смешанное произведение равно нулю, то есть

Нормальный вектор плоскости - это любой ненулевой вектор, лежащий на прямой перпендикулярной к данной плоскости.

Условия параллельности и перпендикулярности плоскостей.

 Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:

.

 

 Плоскости параллельны, векторы нормалей коллинеарны:   .Это условие выполняется, если:  .

31. ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.

Направляющий вектор произвольной прямой в дальнейшем обозначается буквой  , его координаты - буквами l, m, n:

Условия параллельности и перпендикулярности прямых в пространстве

            Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны.

  Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.

32. Угол между двумя плоскостями равен углу между их нормальными векторами. Пусть две пересекающиеся плоскости A₁x + B₁y + C₁z + D₁ = 0 и A₂y + B₂y + C₂z + D₂ = 0 имеют нормальные векторы  =(A₁;B₁; C₁) и  =(A₂; B₂; C₂). Тогда угол между этими плоскостями вычисляется по формуле: 

Угол φ между двумя прямыми, заданными общими уравнениями A₁x + B₁y + C₁ = 0 и A₂x + B₂y + C₂ = 0, вычисляется по формуле: 

Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k₁x + b₁ и y₂ = k₂x + b₂, вычисляется по формуле: 

Угол φ между двумя прямыми, заданными каноническими уравнениями (x-x₁)/m₁ = (y-y₁)/n₁ и (x-x₂)/m₂ = (y-y₂)/n₂, вычисляется по формуле: 

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость

 Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:

.

 

 Плоскости параллельны, векторы нормалей коллинеарны:   .Это условие выполняется, если:  .

Условия параллельности и перпендикулярности двух прямых. Пусть даны две прямые: у1=k1x+b1 и у2=k2x+b2. Если k1= k2, то прямая у1 параллельна у2. Если k1?k2=–1, то данные прямые взаимно перпендикулярны.