Семестр 02 / Шпоры по физике 2 сем / Билеты по физике / Билет 17

1. 1. Математический и физический маятники

В физике под маятником понимают твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.

Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке.

Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити.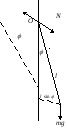

Отклонение маятника от положения равновесия будем характеризовать углом , образованным нитью с вертикалью (см. рис.). При отклонении маятника от положения равновесия возникает вращательный момент N, равный mglsin (m – масса, а l – длинна маятника). Он имеет такое направление, что стремится вернуть маятник в положение равновесия, и аналогичен в этом отношении квазиупругой силе. Поэтому так же, как смещению и квазиупругой силе, моменту N и угловому смещению  нужно приписывать противоположные знаки (рассматривая  как вектор, связанный с направлением поворота правилом правого винта при <<1, противоположность знаков при N и  можно объяснить тем, что векторы N и  направлены в противоположные стороны). Следовательно, выражение для вращательного момента имеет вид: N=-mglsin.

Напишем уравнение динамики вращательного движения для маятника, учитывая, что момент инерции маятника равен ml², а угловое ускорение равно ”, получаем _{. Рассматривая малые колебания можем записать: sin . Введем обозначение} .

_{Тогда мы придем к уравнению: . Очевидно его решение имеет вид: =acos(0t+).}

Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим.

При отклонении маятника от положения равновесия на угол  возникает вращающий момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен: : N=-mglsin, где m – масса маятника, а l – расстояние между точкой подвеса О и центром масс С маятника (см. рис.). Знак “минус” имеет то же значение, что и в случае математического маятника.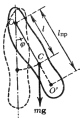

Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать:

_{. В случае малых колебаний} можем переписать уравнение:

_{. В данном случае через} обозначена следующая величина:

Примечание.

Если сравнить значения периодов колебания математического и физического маятника, то можно заметить, что математический маятник длинной l_пр=I/(ml) будет иметь такой период колебаний, как и данный физический маятник. Данную величину называют приведенной длинной физического маятника.

Точка, лежащая на расстоянии приведенной длинны от оси вращения на прямой, соединяющей точку подвеса с центром масс, называется центром качания физического маятника (см. точку O’).

2. Первое начало термодинамики.

При совершении одним телом работы А над другим, равно как и при сообщении одним телом другому теплоты Q, эти тела обмениваются внутренней энергией — энергия одного из тел увеличивается, а энергия другого на столько же уменьшается. Это следует из закона сохранения энер­гии. В термодинамике этот закон принято называть первым началом и записывать следующим образом: Q=U₂—U₁+A (1.5). Здесь U₁ и U₂ - начальное и коночное значения внутренней энергии тела (или системы тел), А - работа, совершенная телом (или системой), Q — количество со­общенной телу (системе) теплоты. Словами первое начало термодинамики формулирует! следующим образом: количество теплоты, сообщенное системе, идет на приращение внутренней энергии сис­темы и па совершение системой работы над внешними телами. Подчеркнем, что речь идет о разности конечного и начального значений внутренней энергии.

При вычислении совершенной системой работы или полученной системой теплоты обычно приходится разби­вать рассматриваемый процесс на ряд элементарных про­цессов, каждый из которых соответствует весьма малому (в пределе — бесконечно малому) изменению параметров системы. Уравнение (1,5) для элементарного процесса имеет вид Q=U+A ,где Q элементарное количество теплоты, A — элементарная работа и U — приращение внутренней энер­гии системы в ходе данного элементарного процесса. Весьма важно иметь в виду, что Q и A нельзя рассматривав как приращения величии Q и А. Соответствующее элементарному процессу  какой-либо вели­чины f можно рассматривать как приращение этой вели­чины только в том случае, если f, соответствующая переходу из одного состояния в другое, не зависит от пути, по которому совершается переход, т.е. если величина f является функцией состояния. В отношении функции со­стояния можно говорить о ее «запасе» в каждом из со­стояний. Например, можно говорить о запасе внутренней энергии, которым обладает система в различных состоя­ниях.

3. Давление идеального газа на стенку.

Стенки сосуда, в котором заключен газ, подвергаются непрерывной бомбардировке молекулами. В результате элементу стенки S сообщается за секунду некоторый им­пульс, который равен силе, действующей на S. Отноше­ние этой силы к величине S дает давление, оказываемое газом на стенки сосуда. Вследствие хаотичности движе­ния молекул давление газа на различные участки стенок сосуда одинаково. Если предположить, что молекулы отскакивают от стенки по закону зеркального отражения и модуль скорости молекулы не изменяется, то им­пульс, сообщаемый при ударе стенке молекулой, будет ра­вен 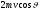(рис.; m — масса молекулы). Этот им­пульс направлен по нормали к площадке. Каждая из молекул сообщает стенке импульс , а все эти мо­лекулы — импульс

Просуммируем полученное выраже­ние по направлениям в пределах телес­ного угла 2. В результате получим импульс, сообщаемый молеку­лами, скорости которых имеют модуль от v до v+dv:

Интегрирова­ние по d дает 2, интеграл по равен 1/3. Следова­тельно, Проинтегрировав это выражение по скоростям от 0 до v_max , получим полный импульс, сообщаемый площадке S за время t: Выражение представляет собой среднее значение квадрата скорости молекул. Заменив в (2.26) интеграл произведением N<v²> получим, что (n=N/V есть число молекул в единице объема). Нако­нец, разделив это выражение на S и t, получим давле­ние газа на стенки сосуда: