Зависимость между коэффициентами искажения. Стандартные аксонометрические проекции. Коэффициенты искажения и углы между осями.
Стандартные аксонометрические проекции
ГОСТ 2.317-69 Аксонометрические проекции
-
I. Прямоугольные:
1) прямоугольная
изометрия;
2) прямоугольная
диметрия.
II. Косоугольные:
1) фронтальная
изометрия;
2) горизонтальная
изометрия;
3) фронтальная
диметрия.
Прямоугольная изометрии и диметрия окружности, лежащей в координатной плоскости. Направление и величина осей эллипсов.
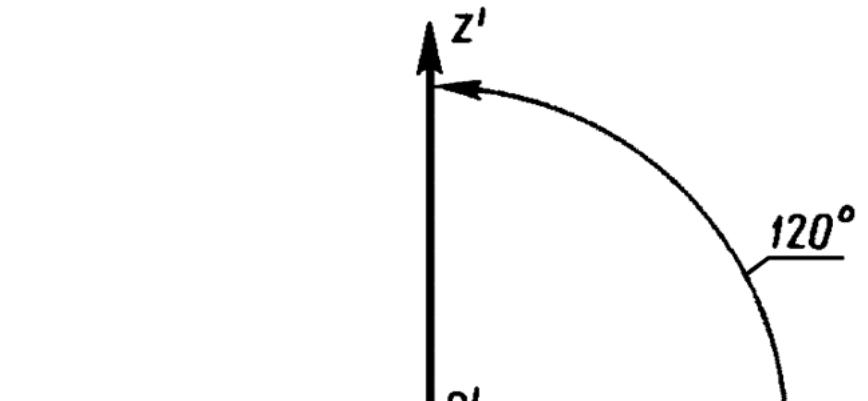
Прямоугольная изометрия
mx=
ny
=pz=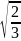
≈0.82
На практике:
mx = ny = pz = 1 – приведенные коэффициенты искажения;
аксонометрический масштаб 1,22:1.
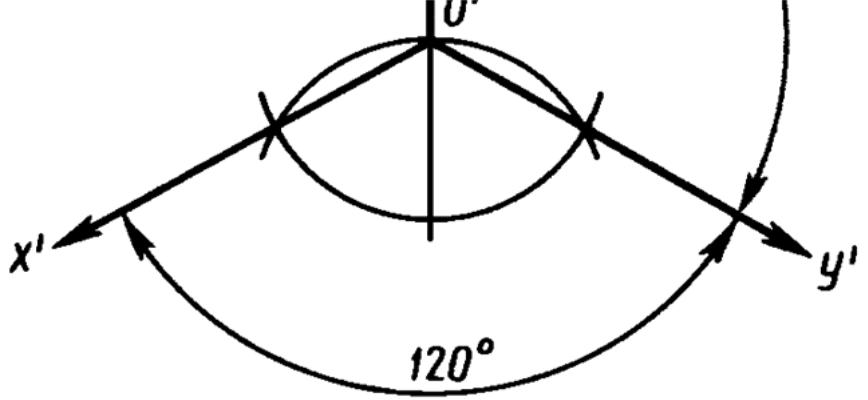
Изометрия окружности
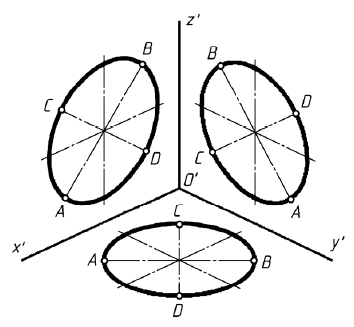
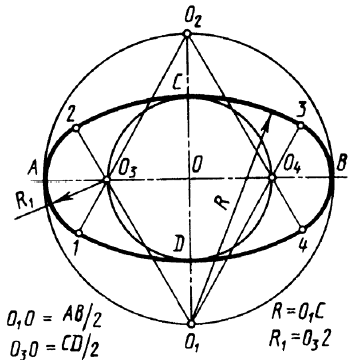
При построении с приведенными коэффициентами искажения:
AB = 1,22d
CD = 0,71d
(d – диаметр окружности)
Касательные линии и плоскости к поверхности.
Прямая линия, касательная к какой-либо кривой линии, принадлежащей поверхности, является касательной и к поверхности.
Касательная плоскость к поверхности есть множество всех касательных, проведенных к поверхности через одну и ту же точку.