
- •Предмет начертательной геометрии. Виды проецирования. Свойства параллельного проецирования. Требования к проекционному чертежу.
- •Эпюр точки в системе трех плоскостей проекций. Ортогональные проекции и система прямоугольных координат. Эпюры точек, расположенных в четвертях и октантах пространства.
- •Прямая. Задание и изображение на чертеже. Положение прямых относительно плоскостей проекций. Следы прямой. Принадлежность точки прямой.
- •Взаимное положение двух прямых: параллельные, пересекающиеся и скрещивающиеся прямые. Конкурирующие точки. Теорема о проецировании прямого угла.
- •Плоскость. Способы задания плоскости на эпюре. Следы плоскости. Положение плоскости относительно плоскостей проекций.
- •Принадлежность точки и линии плоскости. Построение на плоскости прямых общего положения, горизонталей, фронталей и линий ската.
- •Взаимное расположение двух плоскостей. Построение через данную точку плоскости, параллельной данной. Построение линии пересечения плоскостей.
- •Взаимное расположении прямой и плоскости. Построение прямой, принадлежащей плоскости, параллельной плоскости. Построение точки пересечения прямой с плоскостью.
- •Преобразование комплексного чертежа. Способ замены плоскостей проекций. Сущность способа. Замена одной или двух плоскостей проекций. Основные типы задач, решаемых этим способом.
- •Решение метрических задач: определение расстояний; определение углов; построение плоской фигуры по заданным условиям.
- •Кривые линии. Образование, задание и основные свойства проекций плоских и пространственных кривых линий. Образование и построение цилиндрической винтовой линии.
- •Кривые поверхности. Образование, способы задания на чертеже. Определитель, очерк поверхности. Основные типы поверхностей. Принадлежность точки и линии поверхности.
- •Поверхности вращения. Однополостный гиперболоид вращения. Образование и изображение на чертеже.
- •Развертывающиеся линейчатые поверхности. Поверхности с ребром возврата. Образование и изображение на чертеже.
- •Винтовые поверхности. Прямой и наклонный геликоид. Образование и изображение. Применение в технике.
- •Линейчатые поверхности с плоскостью параллелизма: цилиндроиды, коноиды и гиперболический параболоид. Образование, изображение и применение в технике.
- •Многогранники. Образование гранных поверхностей. Видимость ребер. Пересечение призм и пирамид плоскостью.
- •Циклические поверхности.
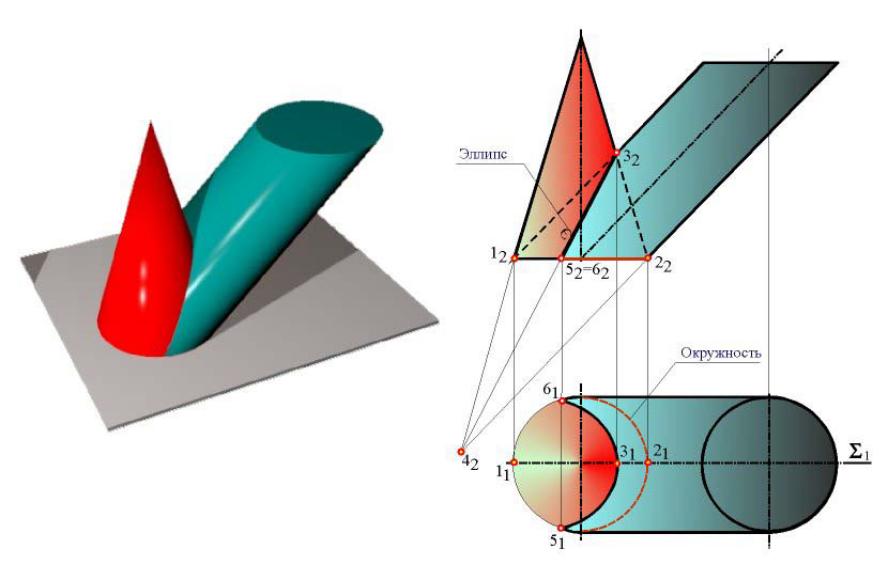
- •Пересечение кривой поверхности плоскостью. Общий метод решения задачи. Конические, цилиндрические и сферические сечения.
- •Пересечение прямой линии с поверхностью. Общий метод решения задачи. Построение точек пересечения прямой с гранной и кривой поверхностью.
- •Взаимное пересечение кривых поверхностей. Общий метод решения задачи. Применение плоскостей общего положения и плоскостей уровня.
- •Пересечение соосных поверхностей вращения. Построение линии пересечения кривых поверхностей с помощью сфер. Теорема Монжа.
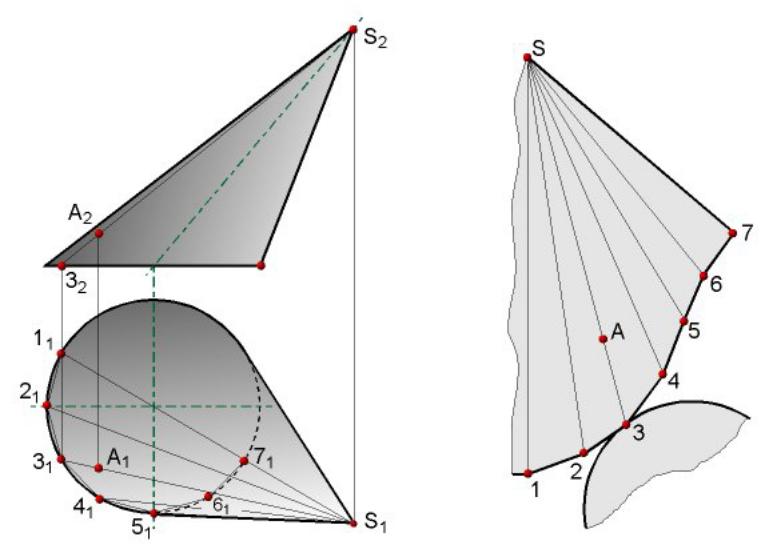
- •Развертка поверхностей. Развертывающиеся и неразвертывающиеся поверхности. Построение развертки пирамиды и наклонной призмы.
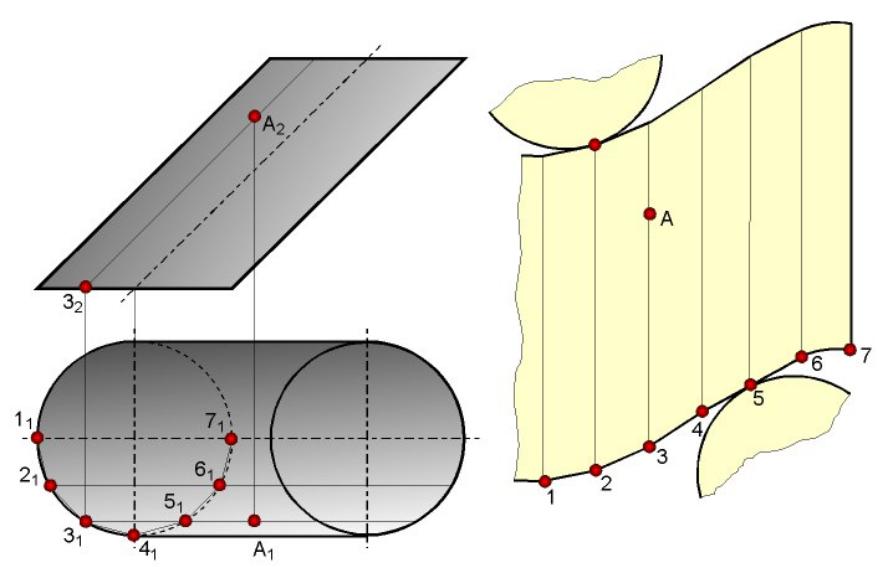
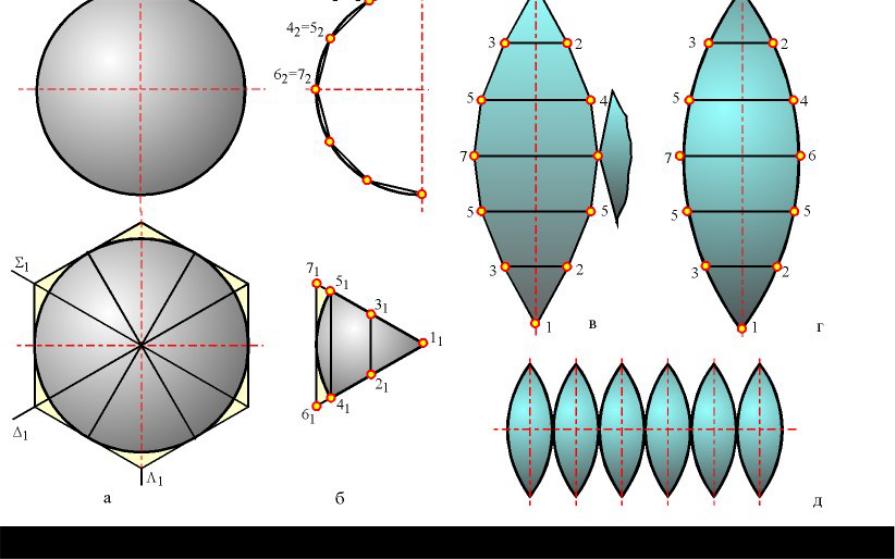
- •Развертка поверхности наклонного конуса и цилиндра. Развертка неразвертывающихся поверхностей.
- •Сущность метода аксонометрического проецирования. Коэффициенты искажения по осям. Виды аксонометрических проекций. Основная теорема аксонометрии.
- •Зависимость между коэффициентами искажения. Стандартные аксонометрические проекции. Коэффициенты искажения и углы между осями.
- •Прямоугольная изометрии и диметрия окружности, лежащей в координатной плоскости. Направление и величина осей эллипсов.
- •Касательные линии и плоскости к поверхности.
Пересечение кривой поверхности плоскостью. Общий метод решения задачи. Конические, цилиндрические и сферические сечения.
Пересечение поверхности плоскостью
При пересечении поверхности плоскостью получается плоская фигура, называемая сечением(плоская кривая).
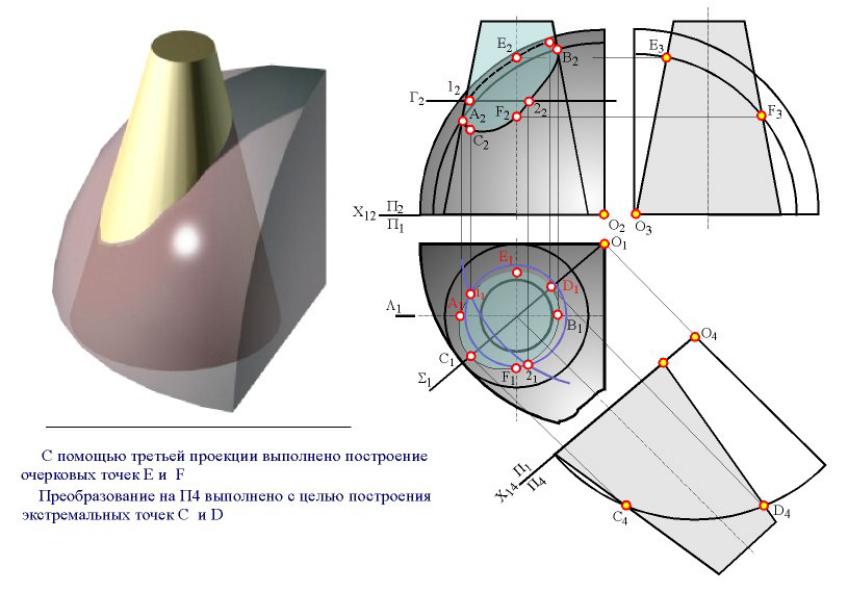
Конические сечения
Сечение конуса вращения плоскостью, перпендикулярной его оси, – окружность.
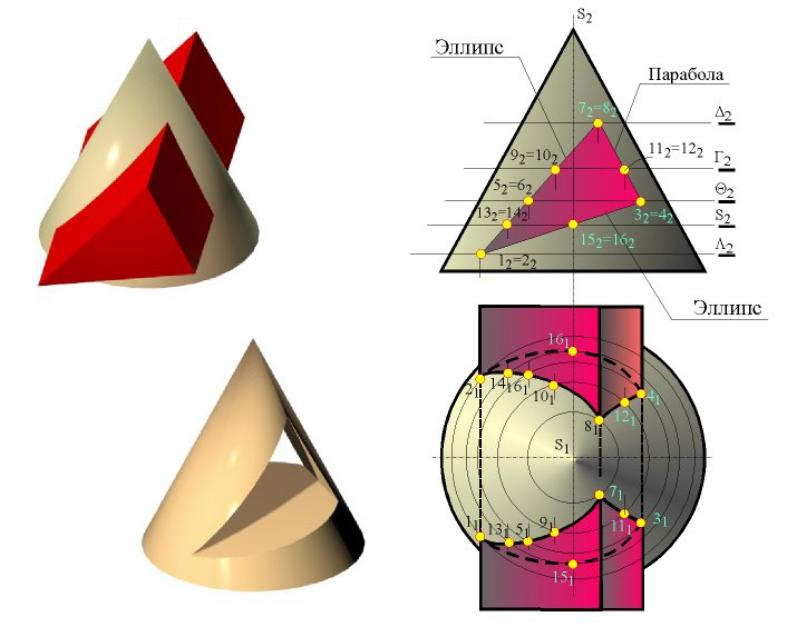
Сечение конуса вращения плоскостью, не параллельной ни одной из его образующих, – эллипс.
Сечение конуса вращения плоскостью, параллельной одной его образующей, – парабола.
Сечение конуса вращения плоскостью, параллельной двум его образующим (в частном
случае – параллельной его оси), – гипербола.
Сечение конуса плоскостью, проходящей через его вершину, – две пересекающиеся
прямые (образующие).
Сечения цилиндра
Сечение цилиндра вращения плоскостью, перпендикулярной его оси, – окружность.
Сечение цилиндра вращения плоскостью, не параллельной ни одной его образующей,
– эллипс.
Сечение цилиндра вращения плоскостью, параллельной его оси, – две параллельные
прямые (образующие).
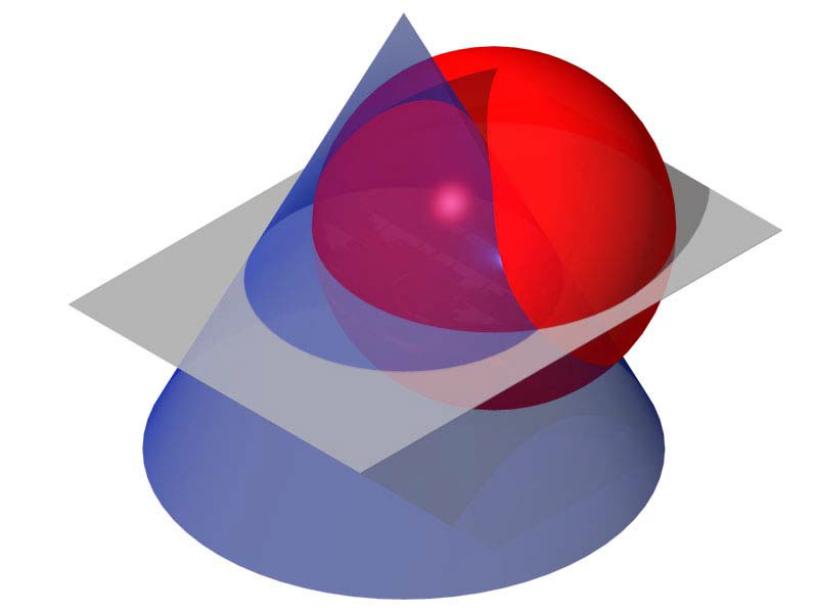
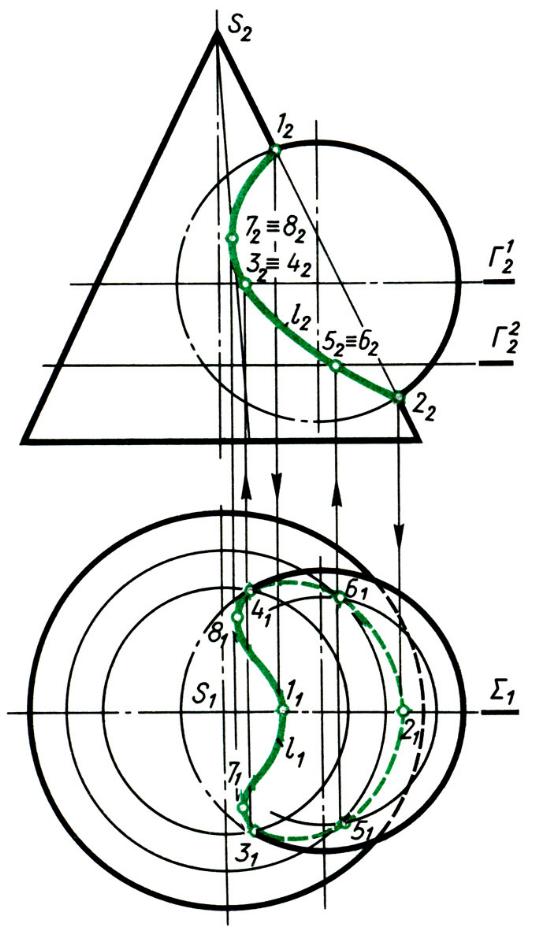
Сечение сферы
Сечение сферы – окружность.
Сечение сферы проецируется в виде окружности, если секущая плоскость параллельна плоскости проекций.
Сечение сферы проецируется в виде эллипса, если секущая плоскость наклонна к плоскости проекций.
Пересечение прямой линии с поверхностью. Общий метод решения задачи. Построение точек пересечения прямой с гранной и кривой поверхностью.
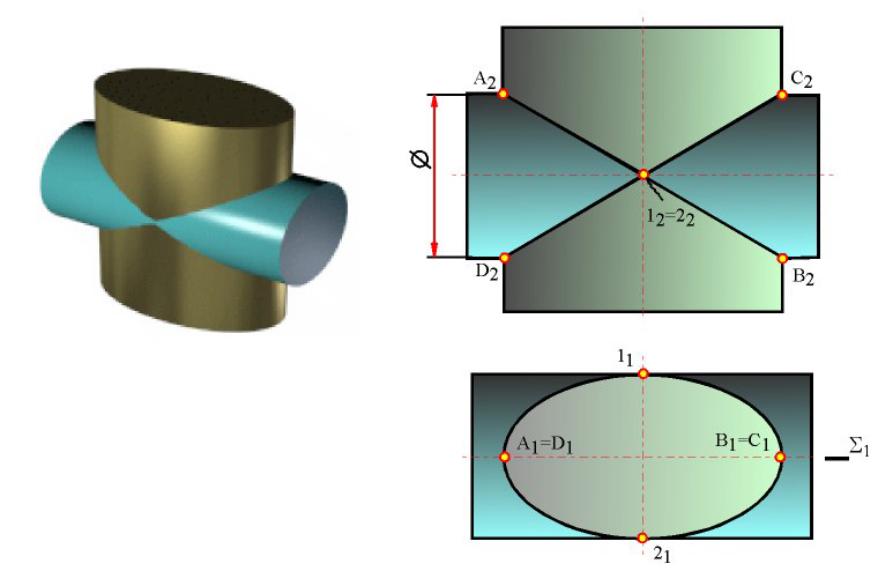
Взаимное пересечение кривых поверхностей. Общий метод решения задачи. Применение плоскостей общего положения и плоскостей уровня.
Построение линии пересечения двух поверхностей
Линия пересечения – в общем случае пространственная кривая линия.
Способ секущих плоскостей.
Пересечение соосных поверхностей вращения. Построение линии пересечения кривых поверхностей с помощью сфер. Теорема Монжа.
Соосными называются поверхности вращения, имеющие общую ось.
Соосные поверхности вращения пересекаются по окружностям.
Способ концентрических сфер

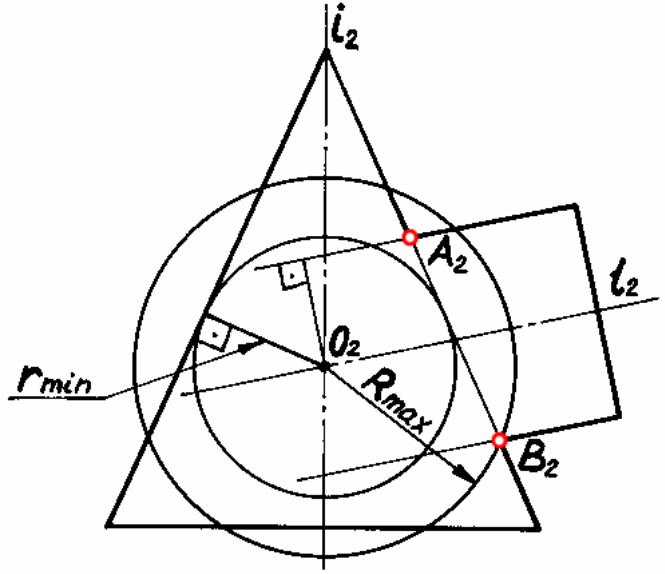
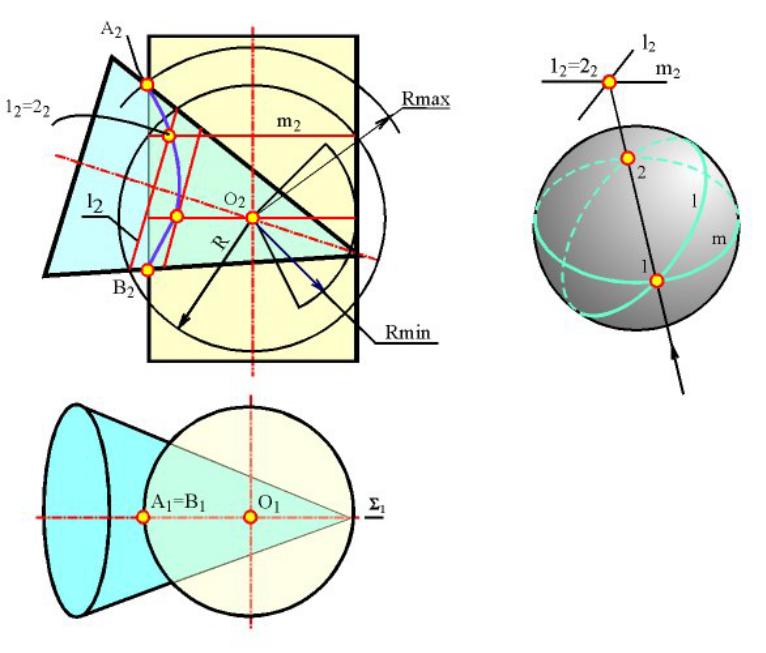
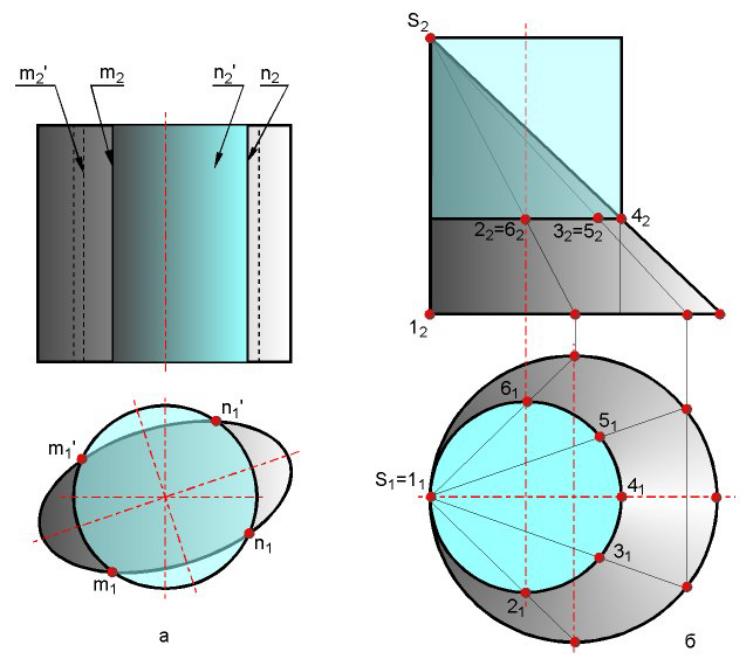
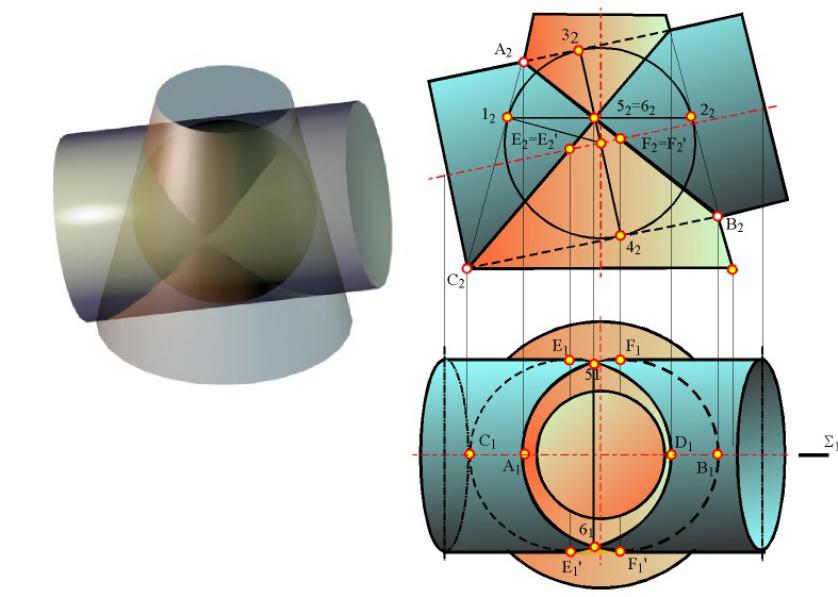
Теорема Монжа
Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.
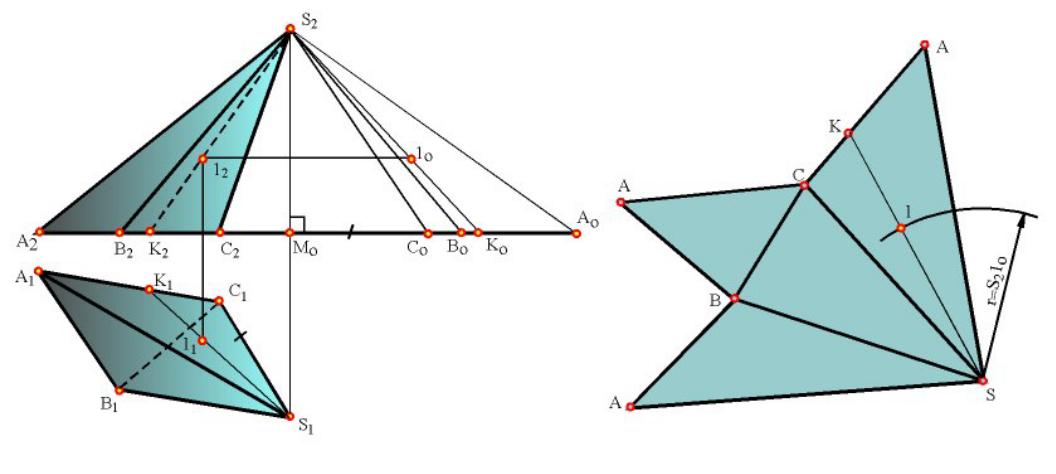
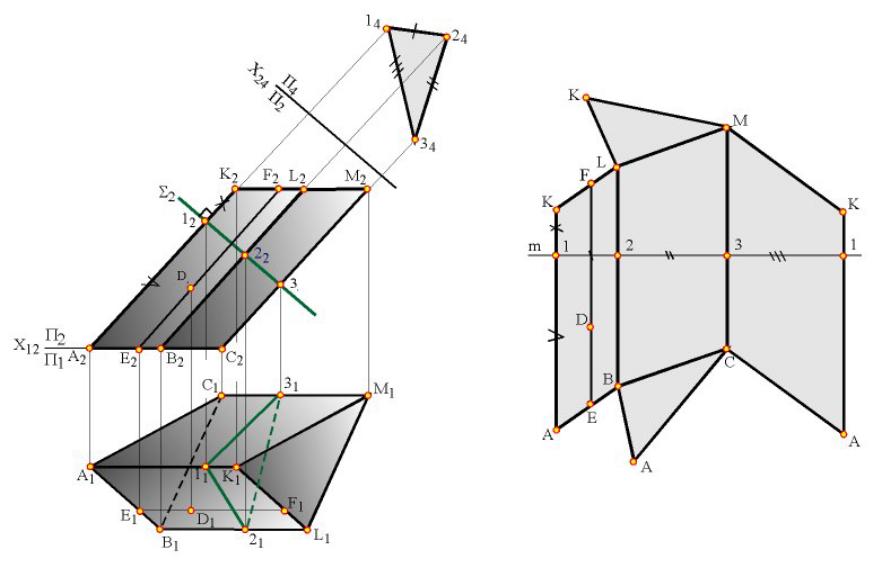
Развертка поверхностей. Развертывающиеся и неразвертывающиеся поверхности. Построение развертки пирамиды и наклонной призмы.
Разверткой называется плоская фигура, полученная в результате совмещения
поверхности с плоскостью.
Развертка поверхности наклонного конуса и цилиндра. Развертка неразвертывающихся поверхностей.
Сущность метода аксонометрического проецирования. Коэффициенты искажения по осям. Виды аксонометрических проекций. Основная теорема аксонометрии.
Аксонометрия – это метод построения изображений параллельным проецированием
предмета вместе с системой координат на одну плоскость.
Достоинство: изображение обладает наглядностью и возможностью измерения по осям и параллельно им.
Коэффициенты искажения
Отношение длины аксонометрической проекции отрезка, взятого по определенной оси или ей параллельно, к истинной длине этого отрезка называется коэффициентом искажения.
mx = ex /e – коэффициент искажения по оси x;
ny = ey /e – коэффициент искажения по оси y;
pz = ez /e – коэффициент искажения по оси z.
m2x +n2y+ p2z= 2 + ctg2ϕ (φ – угол проецирования)
Виды аксонометрических проекций
1. Изометрия (mx = ny = pz)
2. Диметрия (mx = ny ≠ pz)
3. Триметрия (mx ≠ ny ≠ pz , mx ≠ pz)
• прямоугольные (φ = 90°)
• косоугольные (φ ≠ 90°)
