Решение метрических задач: определение расстояний; определение углов; построение плоской фигуры по заданным условиям.
Кривые линии. Образование, задание и основные свойства проекций плоских и пространственных кривых линий. Образование и построение цилиндрической винтовой линии.
Свойства проекций кривых
1. Если точка принадлежит кривой, то проекции точки принадлежат проекциям кривой.
2. Хорда и касательная кривой проецируются соответственно в хорду и касательную
проекции кривой.
Цилиндрическая винтовая линия – пространственная кривая, описываемая точкой при
равномерном движении по прямой, которая равномерно вращается вокруг параллельной ей оси.
Это линия одинакового уклона – гелиса.
Величина перемещения точки вдоль оси за один оборот – шаг винтовой линии h.
α
– угол подъема винтовой линии.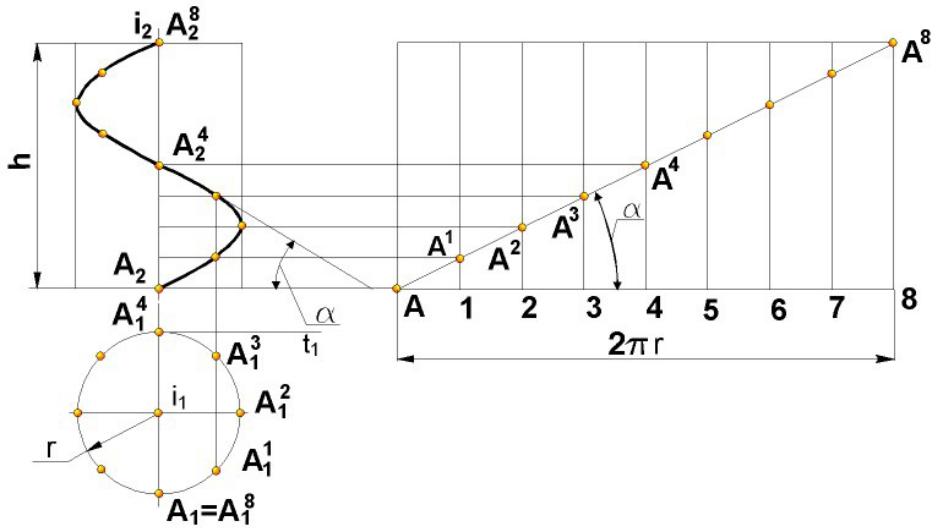
Кривые поверхности. Образование, способы задания на чертеже. Определитель, очерк поверхности. Основные типы поверхностей. Принадлежность точки и линии поверхности.
Образование поверхности
Поверхность образуется перемещением линии в пространстве по определенному закону.
Линия, производящая поверхность, называется образующей.
Образующая при движении может пересекать одну или несколько неподвижных линий, называемых направляющими.
Способы задания поверхностей:
• аналитический – при помощи уравнений;
• при помощи каркаса – множеством линий, принадлежащих поверхности;
• кинематический – перемещением линии в пространстве.
Определитель поверхности – совокупность условий, однозначно задающих поверхность.
Φ (Г) [А]
• Геометрическая часть состоит из совокупности геометрических фигур (точек, линий, плоскостей и т.п.), участвующих в образовании поверхности.
• Алгоритмическая часть (описательная) содержит сведения о характере изменения
образующей и законе ее перемещения.
Очерк поверхности – проекция видимого контура поверхности на рассматриваемую плоскость проекций.
Принадлежность точки поверхности
Точка принадлежит поверхности, если она принадлежит какой-либо линии этой поверхности.
Принадлежность линии поверхности
Линия принадлежит поверхности, если все ее точки принадлежат этой поверхности.
Основные типы поверхностей:
гранные (образующая – прямая, направляющая – ломаная линия);
кривые (кривыми называются поверхности с криволинейной направляющей);
линейчатые поверхности (линейчатыми называются поверхности, образуемые движением прямолинейной образующей):
- развертывающиеся поверхности;
- неразвертывающиеся (косые) поверхности.
Поверхности вращения. Однополостный гиперболоид вращения. Образование и изображение на чертеже.
Поверхности вращения
Образуются вращением образующей – плоской или пространственной кривой линии или прямой вокруг неподвижной оси.
Линейчатые поверхности вращения
Образуются вращением образующей – прямой линии вокруг неподвижной оси.
Например:
цилиндрическая поверхность вращения (образующая – прямая, параллельная оси вращения);
коническая поверхность вращения (образующая – прямая, пересекающая ось вращения);
однополостный гиперболоид вращения (образующая – прямая, скрещивающаяся с осью вращения);
Поверхности, образуемые вращением кривых второго порядка
• вокруг своей оси;
• вокруг оси, не являющейся осью кривой, но расположенной в ее плоскости.
Например:
тор - образуется вращением окружности вокруг оси, лежащей в плоскости окружности, но не проходящей через ее центр;
сфера – образуется вращением окружности вокруг её диаметра;
эллипсоид вращения – образуется вращением эллипса вокруг большой или малой оси;
параболоид вращения – образуется вращением параболы вокруг её оси;
гиперболоид вращения:
- однополостный – образуется вращением гиперболы вокруг её мнимой оси;
- двуполостный – образуется вращением гиперболы вокруг её действительной оси;