Лекция №27 сумматоры и алу

Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и т д. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.

С

КЛАССИФИКАЦИЯ СУММАТОРОВ

ПО СИСТЕМЕ СЧИСЛЕНИЯ

ПО АРХИТЕКТУРЕ

ПО ПЕРЕНОСУ

ПО ЧИСЛУ ОПЕРАНДОВ

Двоичные

Двоично-десятич.

Десятичные

Прочие

Четвертсумматоры

Полусумматоры

Полные сумматоры

С последовательн.

С паралеллным

С групповым переносом

Бинарные

Тринарные

n-арные

умматоры классифицируют по различным признакам.

• четвертьсумматоры, характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма;

• полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноимённые разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (старший разряд);

• полные сумматоры, характеризующиеся наличием трёх входов, на которые подаются одноимённые разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом — перенос в следующий (более старший разряд). Такие сумматоры изначально ориентированы только на показательные позиционные системы счисления.

Основной арифметической операцией, выполняемой любой ЭВМ, является операция суммирования двух n-разрядных кодов (х₁...х_n и у₁...у_n). Суммирование во всех разрядах, начиная с младшего, происходит по единым правилам. В каждом i-м разряде осуществляется сложение х_i+y_i+P_i, где P_i – перенос из младшего i-го в старший разряд. Результат представляется кодами суммы S_i и переноса P_i+1.

Таким образом, сумматор предназначен для арифметического сложения двух чисел. Из принципа сложения многоразрядных двоичных чисел следует, что в каждом i-м разряде находится сумма трех чисел по модулю 2 (слагаемых х_i, y_i и переноса, поступающего из младшего разряда P_i), и формируется сигнал переноса в старший разряд P_i+1.

Для примера проанализируем таблицу истинности одноразрядного сумматора и запишем логические выражения для выходных величин.

	Вход			Выход
	слагаемое		перенос	слагаемое	перенос
i	Хi	Yi	Pi	Si	Pi+1
0	0	0	0	0	0
1	1	0	0	1	0
2	0	1	0	1	0
3	1	1	0	0	1
4	0	0	1	1	0
5	1	0	1	0	1
6	0	1	1	0	1
7	1	1	1	1	1

Логические выражения для выходных величин (формулы S_i и P_i+1 получены из таблицы, где значения S_i и P_i=1):

;

.

В таблице столбцы S_i и P_i+1 заполняются по следующим условиям:

1. P_i+1=1, если не менее 2-х чисел (X_i, Y_i,, P_i)=1;

2. S_i=1, если нечетное число величин Х_i, Y_i, P_i.

Исходя из этих условий, формируется выше представленная таблица истинности работы одноразрядного сумматора.

При разработке функциональной схемы соединение выходов конъюнктора к дизъюнктору определяется из таблицы истинности и согласно характеристическим уравнениям S_i и P_i+1. При этом единица означает, что на вход N должны подать для канала S_i и P_i+1. Именно те сигналы, где выход равен 1. Например:

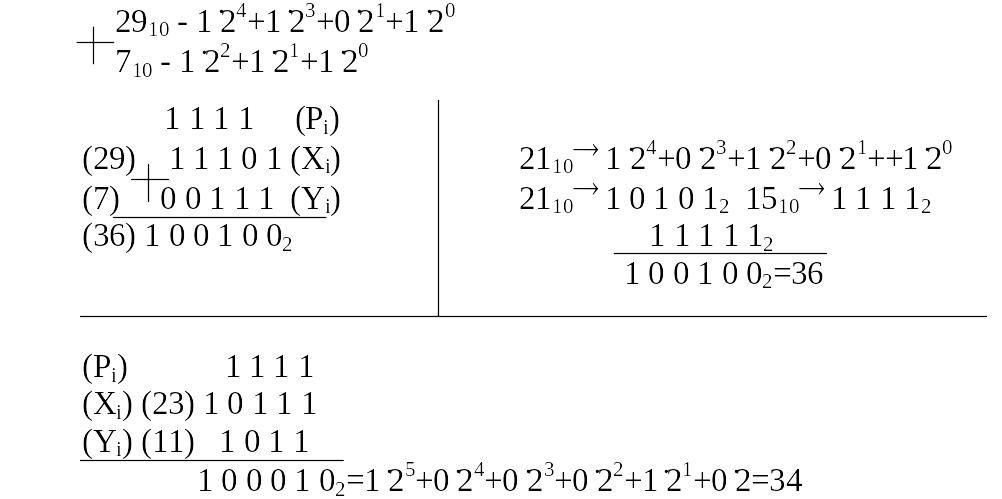
По этим функциям можно построить сумматор на элементах И и ИЛИ.

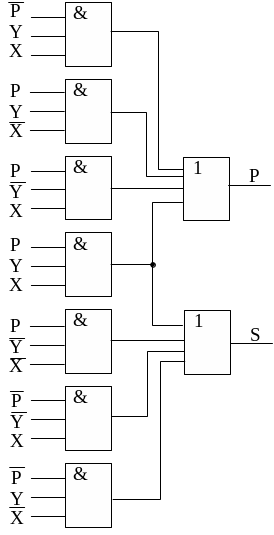
Рис. Сумматор