Лекция №21 план лекции

1.СЧЕТЧИКИ

2. РЕВЕРСИВНЫЕ СЧЕТЧИКИ

3. КОЛЬЦЕВЫЕ СЧЕТЧИКИ

4. ДЕЛИТЕЛИ ЧАСТОТЫ(самостоятельно)

Счетчиком называется автомат, внутренние состояния которого могут циклически изменяться под воздействием одного входного (счетного) сигнала. Следовательно, по начальному и конечному внутренним состояниям автомата можно определить число изменений входного счетного сигнала с 1 на 0, т. е. счетный вход.

Счетчик, как и любой автомат, может иметь только конечное число внутренних состояний, одно из которых выбирается в качестве начального (нулевого) состояния.

По классам цифровых автоматов, на основе теории которых счетчики могут быть синтезированы или описаны, делятся на три большие группы:

1. асинхронные потенциальные;

2. синхронные импульсные;

3. асинхронные импульсные.

В виде ИС выпускаются только синхронные и асинхронные импульсные счетчики.

По способу кодирования внутренних состояний счетчики делятся на подгруппы:

1. двоичные;

2. двоично-десятичные (декадные);

3. счетчики Джонсона;

4. кольцевые счетчики;

5. программируемые счетчики.

С точки зрения разработчика ЭВМ и радиоэлектронной аппаратуры удобно использовать терминологию:

1. суммирующие счетчики (Up-counter);

2. вычитающие счетчики (Down–counter);

3. реверсивные счетчики (Up-down-counter).

Графическое представление разновидности счетчиков можно представить следующим образом.

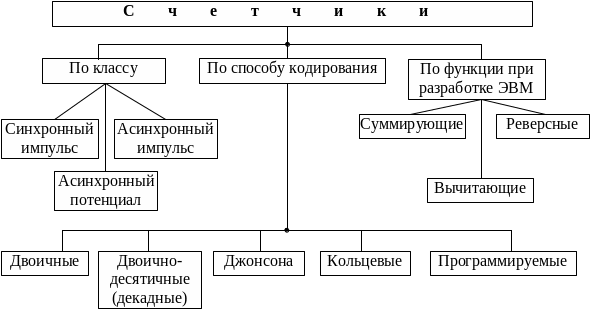
Рис. 12.1 Графическое представление разновидности счетчиков

Кроме 3-х основных способов, описывающих работу цифрового автомата, часто для описания работы счетчика используют графы переходов.

Например, графы переходов двоичного счетчика по mod8 имеет следующий вид.

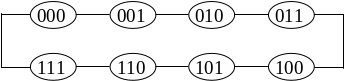
Рис. 12.2 Графы переходов двоичного счетчика по mod8

При этом функция, возбуждая (формула) триггера (ЭП) типа Т, имеет следующий вид.

Q₃=Q₂Q₁, Q₂=Q₁, Q₁=1.

Для m-разрядного счетчика это выражение имеет следующий вид:

, i=2, 3, ..., m.

Для большого размера эта формула упрощается и имеет следующий вид:

, i=2, 3, ...m.

Счетчик – это устройство, обеспечивающее подсчет и преобразование число-импульсного кода в двоичный и двоично-десятичный коды.

Счетчик обычно реализуется на триггерах, имеющих счетный вход. Простейшая схема счетчика с последовательным переносом, построенная на Т-триггерах, представлена на рисунке. Триггер в этой схеме переключается из одного положения в другое при переходе уровня сигнала на счетном входе (С) с высокого на низкий ( ), т. е. от обратного фронта импульса.

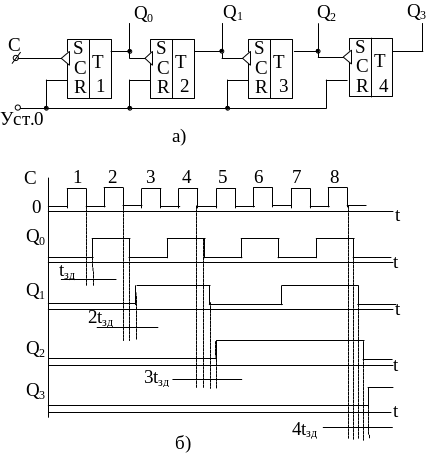
Рис. 12.3 Простейшая схема счетчика с последовательным переносом, построенная на Т-триггерах, и временная диаграмма работы счетчика

На рисунке также приведена временная диаграмма работы счетчика. Кроме основной функции счета импульсов счетчик обеспечивает деление частоты следования импульсов. Если частоту следования импульсов, поступающих на вход Т_i обозначить f, то на выходе триггера T₁ сигнал изменяется с частотой f/2, на выходе триггера Т₂ – f/4, Т₃ – f/8 и т. д.

Обычно счетчик дополняется цепями Уст. 0, шинами выдачи прямого кода Q₀ – Q₃ и т. д.

Таким образом приведенный на рисунке двоичный счетчик делит выходную частоту на 16, т. к. f_вых= f_вх/2ⁿ, где n – количество счетных триггеров.

В настоящее время много двоичных, двоично-десятичных счетчиков и делителей частоты выпускается промышленностью. При этом вся схема размещена в одном корпусе, что создает определенное удобство при конструировании ЭВМ.